Calculando o Momentum de um Ativo Para uma Estratégia de Factor Investing
Nesse meu primeiro artigo de 2022, vou explicar detalhadamente sobre um interessante indicador de momentum, que já possui um screening no nosso site e é muito conhecido por traders de Factor Investing.
Esse indicador foi publicado em 2015 por Andreas F. Clenow, chefe de investimentos da ACIES Asset Management, em seu excelente livro Stocks on the Move. Lá, ele explica a maneira como ele usa esse indicador para montar uma interessante estratégia em um Hedge Fund. No artigo de hoje vamos aprender mais sobre esse indicador.
De uma maneira simplista, indicadores de momentum tem como objetivo identificar ações que estejam mostrando uma tendência de crescimento com a esperança de que essa tendência permaneça por mais um tempo. No QuantBrasil já abordamos com bastante detalhes um famoso indicador de momentum, o IFR.
Mas o que significa momentum?
Recorrendo à física clássica de Sir Isaac Newton, momentum pode ser definido como um vetor correspondente ao produto da massa pela velocidade de uma partícula.
Ainda podemos lembrar que a segunda lei de Newton descreve a força atuante em um objeto como sendo a derivada do momentum em relação ao tempo. E além disso, a primeira lei de Newton, conhecida também como lei da inércia, diz que todo corpo parado tende a ficar parado e todo corpo em movimento tende a permanecer em movimento com a mesma velocidade e direção (claro, se forças externas não forem aplicadas a ele).
Tá bom, mas o que isso tem a ver com o indicador de momentum?
Tudo! A ideia derivada por Sir Newton para descrever a física no século XVII pode ser utilizada e aplicada ao movimento de ações no mercado financeiro.
O objetivo é buscar ações que estejam em uma tendência de alta, e assim como na primeira lei de Newton, esperar que elas permaneçam com essa tendência.
Mas lembre-se, assim como nas leis da física, no Mercado Financeiro as regras são as mesmas: as ações só irão se manter na mesma tendência se não existissem "forças externas". E como bem sabemos, o mercado financeiro é muito afetado por forças externas.
Por isso que devemos sempre testar estratégias baseadas em indicadores da análise técnica e definirmos conscientemente pontos de saída e stop loss para não sermos pegos de surpresa quando as tendências mudam.
Uma estratégia simples então seria usar esse indicador para selecionar de um determinado universo de ativos, as que possuem melhor "momentum".
Então a estratégia consiste em ranquear ações por esse tal de momentum e comprar as que estão no topo?
Exatamente! Contudo, um ponto importante levantado por Andreas em seu livro é a volatilidade. A idéia não é apenas selecionar as ações que tiveram uma maior retorno absoluto em um ano, mas sim determinar quais delas apresentam um melhor retorno/volatilidade. Ou seja, essa estratégia visa maximizar performance com o menor risco possível.
Sem mais delongas, vamos aprender os conceitos matemáticos por trás desse indicador e como programá-lo em Python.
As bibliotecas que vamos precisar para os nossos cálculos serão importadas abaixo.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegressionPara esse estudo, vamos pegar como exemplo as ações da JBS no timeframe diário desde o ínicio do ano de 2019. Esses dados estarão disponíveis no nosso grupo do Telegram.
df = pd.read_csv('../data/D1/JBSS3-D1-momentum.csv', index_col='datetime', parse_dates=True)[['close']]
df.columns = ['JBSS3']
df
| JBSS3 | |
|---|---|
| datetime | |
| 2019-01-02 | 12.04 |
| 2019-01-03 | 12.23 |
| 2019-01-04 | 12.55 |
| 2019-01-07 | 12.11 |
| 2019-01-08 | 12.30 |
| ... | ... |
| 2022-01-10 | 35.90 |
| 2022-01-11 | 35.71 |
| 2022-01-12 | 36.43 |
| 2022-01-13 | 37.06 |
| 2022-01-14 | 37.87 |
754 rows × 1 columns
A ideia por trás do indicador
Para o cálculo do momentum em si, tudo que temos que fazer é uma regressão. Para quem está acompanhando a nossa série sobre long & short por cointegração ou tenha lido o artigo sobre o beta já sabe que regressão linear é uma forma de ajustar um determinado conjunto de dados, minimizando o erro de cada ponto, utilizando uma reta.
O coeficiente angular (ou inclinação) dessa reta vai nos dizer quanto (em valores absolutos) a ação deveria se movimentar por dia. Em outras palavras, a inclinação pode ser vista como uma medida de velocidade ou momentum do preço de uma ação.
Contudo, note que eu disse que para o cálculo de momentum, precisamos apenas de uma regressão mas eu não mencionei especificamente linear. Em seu livro, Andreas sugere o uso da regressão exponencial ao invés da famosa linear. A razão dessa preferência é simples: em uma regressão linear, a inclinação da reta é dada em valores absolutos, e isso não leva em consideração o preço da ação.
Vamos olhar um exemplo para entender melhor. Suponha que a ação da JHSF3 (que está cotada a mais ou menos R$4,50) subiu 1 real em um determinado dia, e a ação da VALE3 (mais ou menos R$82,80) subiu 1 real também. Embora ambas tenham subido a mesma quantia, qual que valeu mais a pena?
Claramente a JHSF3 obteve um maior ganho percentual. E é exatamente por isso que Andreas prefere usar uma regressão exponencial. Diferentemente do coeficiente angular da reta, que fornece os valores em unidades absolutas da moeda em questão, o coeficiente exponencial nos retorna o valor em porcentagem! Ou seja, conseguimos identificar o percentual médio do movimento de uma ação por dia.
Para evitar o problema de nos depararmos com valores percentuais muito baixos, Andreas sugere anualizar esse coeficiente. Assim, obtemos um valor que nos diz quanto uma ação iria ganhar ou perder ao longo de 1 ano se esse coeficiente se mantivesse o mesmo ao longo desse período.
Obviamente esse é um valor teórico, que provavelmente não será obtido ao final do ano. Contudo, Andreas argumenta que dessa forma pode-se trabalhar com números que são de fácil compreensão.
Nas próximas seções, vamos aprender como calcular ambas as regressões, de modo que você poderá escolher a que mais se adequar ao seu caso de uso.
Por último, lembra que eu comentei sobre a volatilidade no começo desse post? A estratégia de momentum visa evitar comprar ações que tiveram um salto grande e repentino no preço. A ideia é selecionar um momentum real e não artificial gerado por alta volatilidade.
Para resolver essa questão, uma solução seria punir as ações que possuem alta volatilidade, empurrando elas para baixo da nossa lista. Mas como fazer isso?
Penalizando ações com alta volatilidade
Existe uma solução simples para realizar esse passo: utilizar o coeficiente de determinação, também conhecido como , da regressão. Esse valor nos ajuda a entender o quanto a nossa curva se ajusta aos nossos dados.
Por exemplo, se os dados estiverem espalhados aleatóriamente, o nosso será próximo de 0, pois nossa curva descreve muito mal um comportamento aleatório.
Contudo, quanto mais os nossos dados se aproximarem da nossa curva, maior será o valor do . Se a curva aproximar perfeitamente os dados, chegamos no caso ótimo de .
Confuso? Calma que vamos entender melhor com o exemplo abaixo.
Primeiro vamos gerar dados aleatórios usando a função random.randit do NumPy. Por simplicidade, vamos utilizar apenas 5 valores inteiros no intervalo de 20 a 100.
data_random = np.random.randint(20, 100, size=5)
data_random
array([42, 66, 41, 25, 93])Com esses dados em mãos, vamos criar um intervalo linearmente espaçado para que cada dado anterior possa ser representado por um valor. Esse intervalo será a nossa variável independente, normalmente representada em dias. Para isso, utilizamos a função arange fornecendo o quantidade de valores que queremos (nesse caso, a quantidade de elementos no nosso array).
x = np.arange(len(data_random))
x
array([0, 1, 2, 3, 4])Perfeito, agora podemos facilmente plotar esse conjunto de dados usando a opção scatter do matplotlib.
plt.scatter(x, data_random)
plt.show()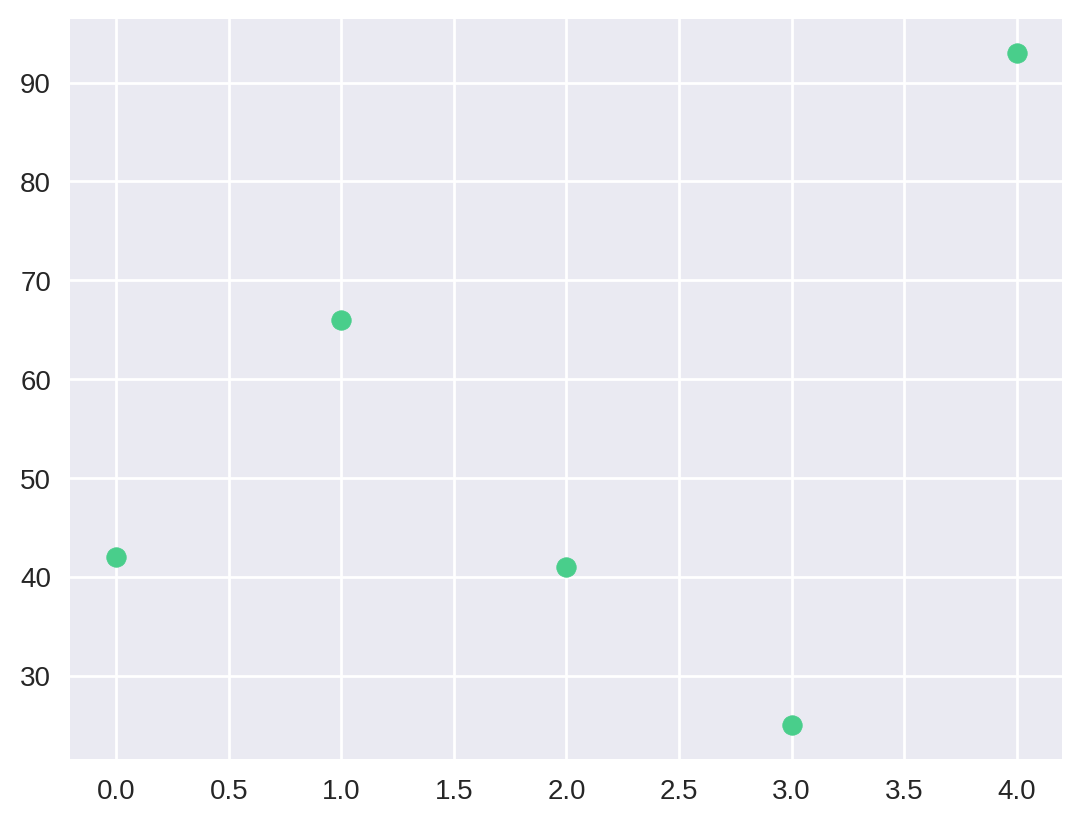
Como esperado, os dados estão distribuidos no nosso gráfico sem nenhum padrão. Vamos agora tentar aproximar esses dados por uma reta. Para isso, vamos programar rapidamente uma função que calcula a regressão linear dado um conjunto de pontos.
Lembre-se que a função LinearRegression necessita de um array bi-dimensional como parâmetro de entrada. Por isso, temos que re-formatar os nossos dados usando a função reshape. Para mais detalhes, leia o nosso post sobre o beta na parte de regressão linear.
O coeficiente de determinação pode ser facilmente obtido utilizando o método score nos nossos dados.
Nossa função vai então retornar o valor do junto com os valores da reta que melhor tenta aproximar os dados.
def linear_regression(x, data):
# reshape the series to use in the linear regression
x = x.reshape(-1, 1)
y = data.reshape(-1, 1)
# call the function to calculate the regression
reg = LinearRegression().fit(x, y)
# get the R²
r2 = reg.score(x, y)
# return the predicted fit for our values of x
return r2, reg.predict(x)Com nossa função programada, podemos chama-la e imprimir o valor do arredondado para 3 casas decimais.
r2, linear_fit = linear_regression(x, data_random)
print(f'R² = {r2:.3f}')R² = 0.132
Note que o valor do é bem pequeno e próximo de 0. Isso significa que nossos dados (que são aleatórios) não são bem descritos por uma reta. Para facilitar a visualização, vamos plotar os dados junto com a reta obtida.
plt.scatter(x, data_random, color="black")
plt.plot(x, linear_fit, color="blue", linewidth=2)
plt.show()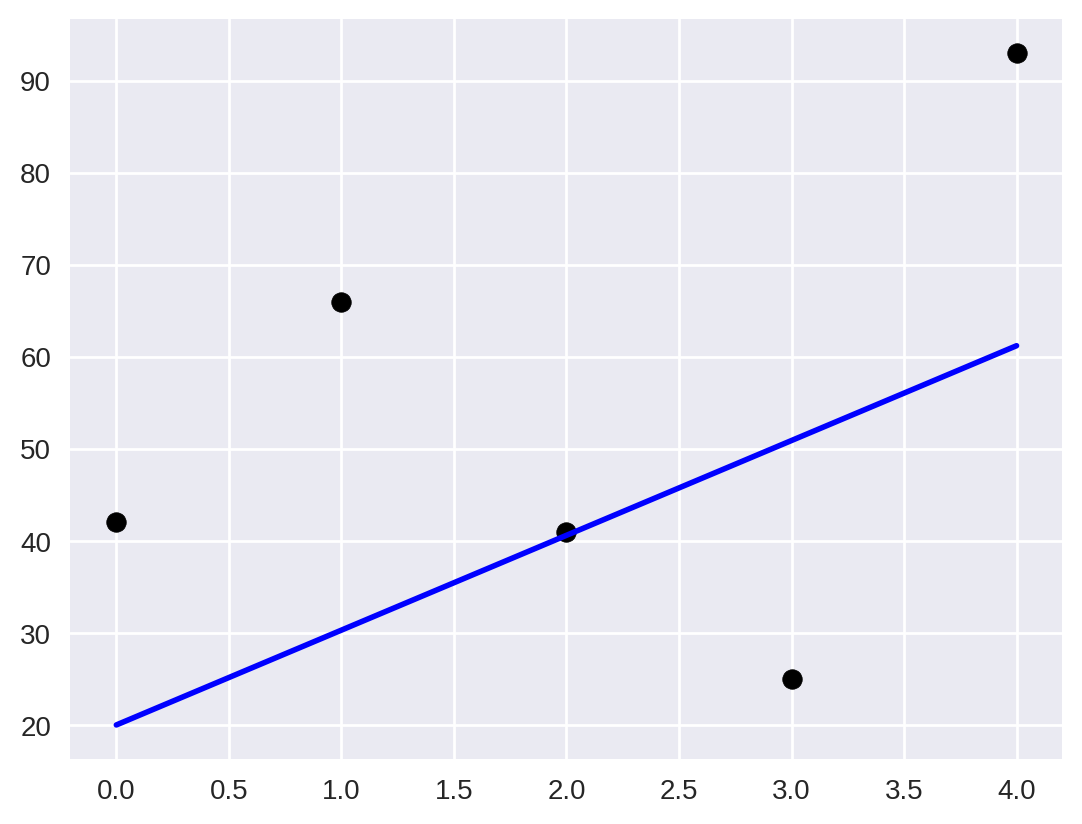
Podemos então observar graficamente o que o valor do já tinha nos dito: uma reta não é uma boa aproximação dos nossos dados.
Contudo, vamos agora criar um array contendo valores que crescam quase que linearmente, apenas com um pequeno desvio.
data_quasi_linear = np.array([20,31,39,52,61])
data_quasi_linear
array([20, 31, 39, 52, 61])Como já criamos a função que calcula a regressão, podemos apenas chamá-la novamente, dessa vez utilizando o novo conjunto de dados.
r2, linear_fit = linear_regression(x, data_quasi_linear)
print(f'R² = {r2:3f}')R² = 0.995963
Dessa vez o valor do está muito próximo de 1, mostrando que a nossa função representa quase que perfeitamente o novo conjunto de dados.
plt.scatter(x, data_quasi_linear, color="black")
plt.plot(x, linear_fit, color="blue", linewidth=2)
plt.show()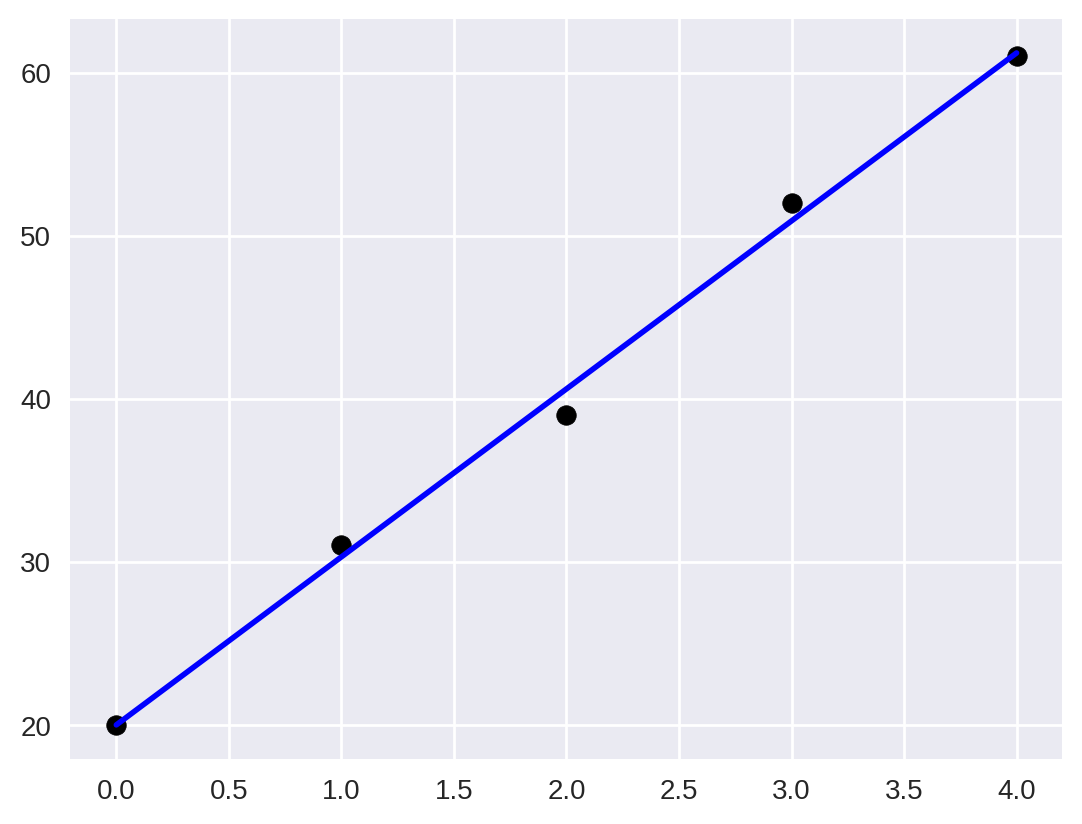
De fato os dados estão todos praticamente em cima da reta, o que a torna uma ótima aproximação dos valores.
Então se quanto pior a aproximação mais perto de 0 é o valor do e quanto melhor a aproximação mais perto de 1, a sacada agora é simplesmente multiplicar o nosso valor de momentum pelo valor do . Com isso, nós conseguimos definir uma maneira matemática de punir as ações com alta volatilidade.
De uma maneira resumida, precisamos efetuar os seguintes passos:
- Calcular uma regressão (linear ou exponencial) para as variações de preço diárias de um ativo nos últimos X dias;
- Anualizar o coeficiente angular dessa regressão;
- Multiplicar o coeficiente anualizado pelo valor do coeficiente de determinação ().
Pronto, esses são os passos para calcular o momentum! Normalmente, o período de tempo escolhido para a regressão é de 90 dias.
Programando o indicador de momentum
Para realizar os passos descritos anteriormente, vamos programar uma função que vai receber os dados diários de variação de um ativo e o tipo de regressão desejada (linear ou exponencial) e retornar o valor do momentum anualizado corrigido pela volatilidade.
Para de fato calcularmos a regressão exponencial, precisamos tirar o log da nossa variável dependente, y, que no nosso caso representa a variação diária do ativo. Para a nossa variável independente, x, criamos novamente um vetor linearmente espaçado representando o número de dias.
def calculate_asset_momentum(df, regression='linear'):
# reshape the series to use in the linear regression
y = df.iloc[:].values.reshape(-1, 1)
# take the log if exponential regression is wanted
if regression == 'exp':
y = np.log(y)
# create a linear spaced vector corresponding to days
x = np.arange(len(y)).reshape(-1, 1)
# call the function to calculate the regression
reg = LinearRegression().fit(x, y)
# get the angular coeff (beta) and the R²
beta = reg.coef_
r2 = reg.score(x, y)
# calculate anualised momentum: a year has approx 252 trading days
if regression == 'exp':
momentum = (np.exp(beta * 252) - 1) * r2
else:
momentum = beta * 252 * r2
return momentumVeja que conseguimos obter facilmente o coeficiente angular e de determinação chamando .coef e .score, respectivamente.
Para anualizar o coeficiente , precisamos levar em consideração qual regressão estamos usando.
Se a angulação da regressão linear nada mais é do que o valor absoluto que a ação é esperada de variar em 1 dia, para descobrir quanto ela é esperada de variar em 1 ano basta multiplicarmos pela quantidade aproximada de pregões em 1 ano, 252.
Contudo, para a regressão exponencial, um passo a mais é necessário pois temos que converter o coeficiente de volta aplicando a função exponencial no nosso coeficiente anualizado.
Finalmente, como queremos penalizar as regressões que não se “encaixam” muito bem na reta, multiplicamos pelo .
Aplicando o indicador de momentum em JBSS3
Agora podemos chamar a função que programamos escolhendo a nossa ação (JBSS3) e o número de dias (90) que queremos analisar.
Vamos criar duas colunas, linear e exp, para armazenarmos os valores do momentum calculados utilizando cada regressão.
ticker = 'JBSS3'
days = 90
df[ticker + '_linear'] = df[ticker].rolling(days).apply(calculate_asset_momentum)
df[ticker + '_exp'] = df[ticker].rolling(days).apply(calculate_asset_momentum, args=('exp',))
df
| JBSS3 | JBSS3_linear | JBSS3_exp | |
|---|---|---|---|
| datetime | |||
| 2019-01-02 | 12.04 | NaN | NaN |
| 2019-01-03 | 12.23 | NaN | NaN |
| 2019-01-04 | 12.55 | NaN | NaN |
| 2019-01-07 | 12.11 | NaN | NaN |
| 2019-01-08 | 12.30 | NaN | NaN |
| ... | ... | ... | ... |
| 2022-01-10 | 35.90 | 5.565268 | 0.204763 |
| 2022-01-11 | 35.71 | 4.803752 | 0.174576 |
| 2022-01-12 | 36.43 | 4.213567 | 0.151233 |
| 2022-01-13 | 37.06 | 3.747018 | 0.132735 |
| 2022-01-14 | 37.87 | 3.342914 | 0.116277 |
754 rows × 3 columns
Os primeiros valores são NaN pois precisamos de 90 dias para podermos começar os cálculos. Note também que utilizamos a função .rolling junto com .apply pois estamos sempre re-calculando o valor do momentum para os últimos 90 dias.
Para melhor visualizar os resultados, vamos plotar o valor da ação junto com os seus valores de momentum em um gráfico.
# Plot the stock price with its anualised exp and linear momentum
fig, (ax1, ax2, ax3) = plt.subplots(
nrows=3,
sharex=True,
figsize=(14,10),
gridspec_kw={'height_ratios': [3, 1, 1]})
# Plot stock price
ax1.plot(df.index, df[ticker], label='JBSS3')
ax1.legend()
# Plot exp momentum
ax2.plot(df.index, df[ticker + '_exp'], label='Annualized exp momentum', color="#033660")
ax2.legend()
# Plot linear momentum
ax3.plot(df.index, df[ticker + '_linear'], label='Annualized linear momentum', color="#033660")
ax3.legend()
plt.show()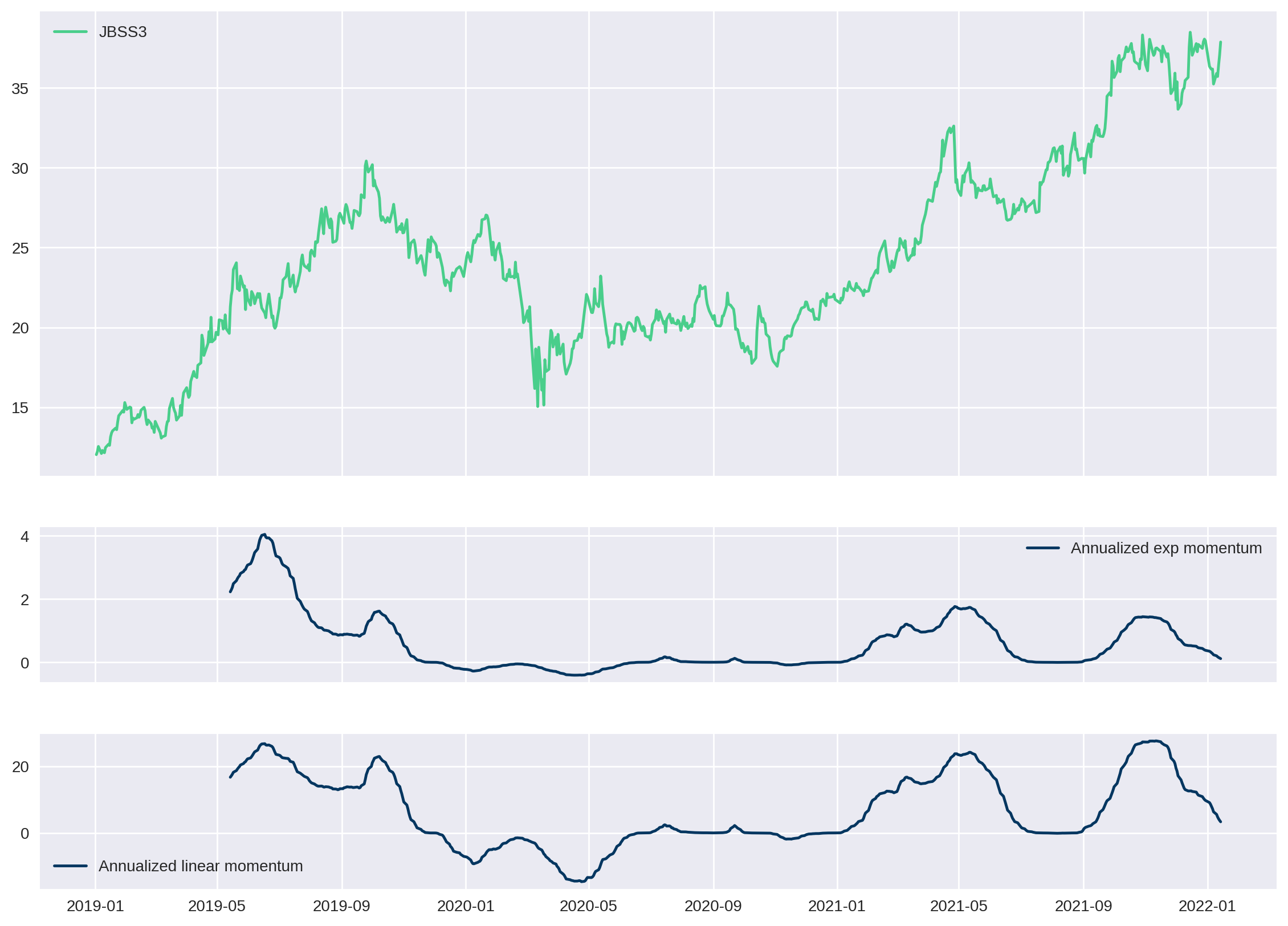
Como esperado, os primeiros 90 dias do momentum não são plotados pois não possuem nenhum dado.
A forma das duas curvas, seja linear ou exponencial, é muito parecida; começa subindo quando a ação vai ganhando força, fica baixa quando a ação está de lado mas volta a subir quando a ação ensaia uma recuperação maior e duradoura.
Contudo note que a curva de momentum linear é mais sensível que a exponencial. Em outras palavras, quando a curva linear sobe, ela sobe com mais força do que a regressão exponencial. Isso fica claro durante os meses 09/2019, 05/2021 e 09/2021.
Importante notar também que embora a ação tenha subido no final do ano de 2021, seu momentum acabou caíndo. Essa informação é bastante importante também para perceber que momentum não é apenas uma curva de tendência. Nesse caso, como estamos punindo pela volatilidade dos últimos 90 dias, o valor de momentum acaba caindo nessa parte.
Conclusão e próximos passos
No artigo de hoje aprendemos o que é o momentum e como calcular o indicador idealizado por Andreas F. Clenow em seu livro. Agora que você já entendeu o conceito e a matemática por trás desse indicador, você já vai se sentir mais confortável para utilizar o nosso screening de momentum!
Nos próximos artigos, vamos aplicar esse indicador para ranquear os 200 ativos mais líquidos da bolsa e também fazer o backtest da estratégia proposta por Andreas em seu livro.
Por isso, não se esqueça de criar a sua conta no nosso site e entrar no nosso grupo do Telegram para ficar por dentro de tudo que rola aqui no QuantBrasil.
Um abraço!
Inscreva-se no canal do QuantBrasil!
Acompanhe novidades sobre a plataforma, vídeos sobre finanças quantitativas, tutoriais sobre programação e Inteligência Artificial!