Aprenda a Estratégia de Long & Short por Cointegração
Hoje vamos dar inicio à uma estratégia muito interessante que é muito utilizada no exterior mas que vem crescendo cada vez mais em popularidade no Brasil: Long & Short (L&S) pelo método da cointegração. Mas antes de começarmos, é importante esclarecer o que significa cada uma dessas palavras.
O que é Long & Short?
Quando você está comprado em um determinado ativo A na sua carteira que você acredita que vai se valorizar com o tempo, você está long (comprado) nesse ativo.
O oposto disso é estar short (vendido). Nesse caso, você ganha dinheiro quando um determinado ativo B se desvaloriza.
Essas duas operações podem ser performadas separadamente: você pode só estar comprado no ativo A ou apenas vendido no ativo B. Contudo, existe também a possibilidade de se aproveitar as relações entre dois ativos e, com o dinheiro recebido por vender o ativo B, comprar o ativo A. Nesse caso, a operação recebe o nome de Long & Short.
Séries Estacionárias e Não-Estacionárias
Tradicionalmente, as operações de L&S se baseiam no método da correlação. Esse método busca algum tipo de dependência linear entra duas variáveis independentes. Por exemplo, se dois ativos estão correlacionados, uma variação em um ativo A corresponde a uma variação na mesma direção do ativo B (caso a correlação seja positiva), ou em sentidos opostos (caso a correlação seja negativa).
No entanto, a correlação não leva em consideração a variação dos dados (também chamadas de séries) com o tempo. Para que uma estratégia de Long & Short possa ser aplicada, é preciso determinar se a série é estacionária no tempo.
Uma série estacionária é toda série cujas propriedades estatísticas como média, variância ou covariância não variam com o tempo. Logo, o oposto disso é chamado de série não-estacionária, ou seja, séries que possuem média, variância e covariância dependentes do tempo.
Para entender melhor o conceito de estacionariedade, vamos considerar o simples exemplo abaixo, onde pegamos do Google Trends o número de vezes que a palavra cupcake foi pesquisada no Google durante os anos de 2004 e 2007.
import pandas as pd
import numpy as np
import matplotlib.pyplot as pltdata = pd.read_csv('../data/cup-cake.csv', header=0,index_col=0)
mean = data['Cupcake:(Worldwide)'].mean()
data.plot(figsize=(10,6))
plt.axhline(y=mean, color="red", linestyle='-')
plt.show()
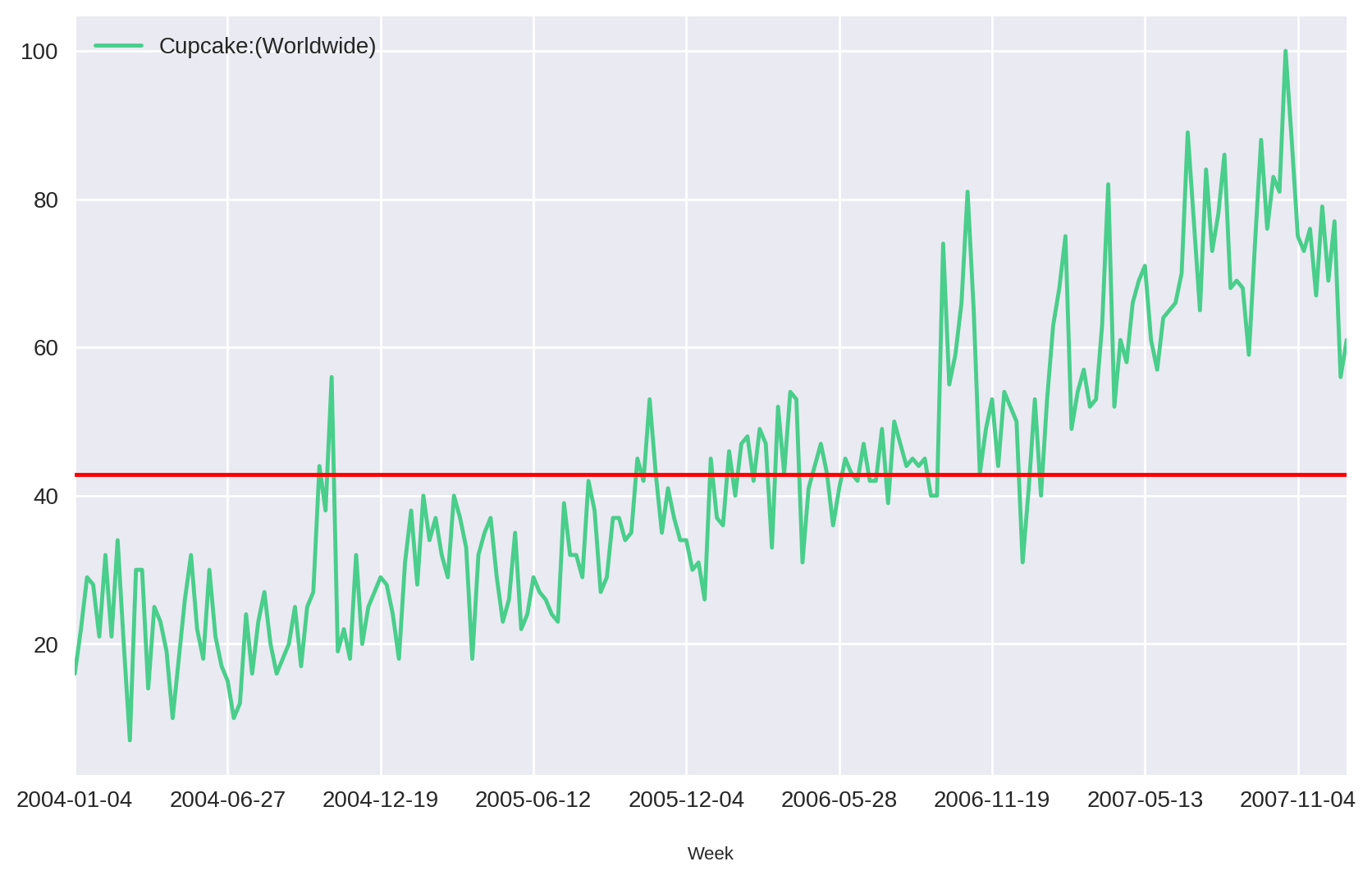
Para facilitar a interpretação, adicionamos a média (em vermelho). Nesse exemplo, vemos que a série não oscila em torno da média e que ela parecer ter uma tendência de crescimento linear com o tempo. À medida que formos adicionando valores a essa série, a sua média (e, consequentemente seu desvio padrão, variâcia, etc) vai mudando de valor. Essa série então é definida como uma série não-estacionária.
Uma forma de remover a tendência do gráfico é através do método da diferenciação. Esse método consiste em simplemente subtrair do valor atual o valor anterior.
data_diff = data.diff()
mean_diff = data_diff['Cupcake:(Worldwide)'].mean()
data_diff.plot(figsize=(10, 6))
plt.axhline(y=mean_diff, color='red', linestyle='-')
plt.show()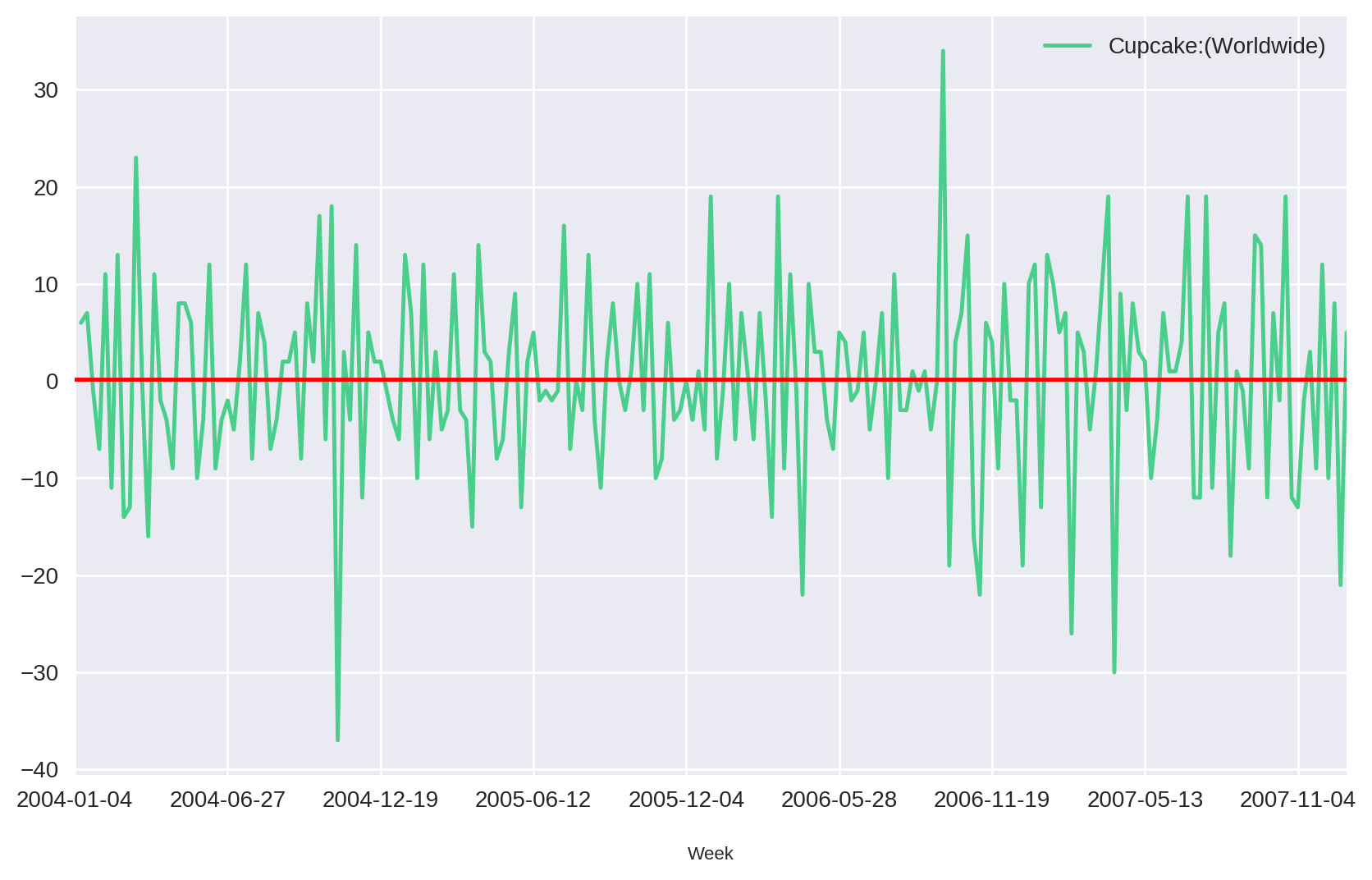
Comparando as duas séries, podemos perceber que os valores oscilam em torno de zero independentemente do tempo.
À medida que mais valores forem adicionados à série, a média e outras propriedades estatísticas continuarão constantes. Com isso, conseguimos transformar a nossa série em uma série estacionária.
Obviamente, nem sempre as tendências existentes em séries não-estacionárias serão facilmente removidas como no exemplo acima (muitas vezes não sendo nem possível). Portanto, o processo de identificação e limpeza dos dados constitui uma grande (e importante) parte da análise.
Estacionariedade de preços
Agora que já entendemos a definição de uma série estacionária, é simples perceber que os preços dos ativos são fortemente dependentes do tempo e, portanto, são não-estacionárias. Por conta disso, um erro clássico em estratégias de L&S é assumir que um par de ativos irá regredir à média. Ora, mas isso só poderia ser assumido se a série fosse estacionária, o que nós já entendemos que não é!
Você pode estar então se perguntando: "se os ativos sempre variam com o tempo, como podemos tirar essa dependência para aplicarmos modelos estatisticamente consistentes?" Ótima pergunta! É aí que entra o conceito de cointegração.
A cointegração consistem em analisar o resíduo de uma regressão linear entre os ativos e procurar por estacionariedade nele. "Mas o que é resíduo? Como eu faço essa regressão linear? Como eu vou saber se uma série é estacionária ou não?"
Calma, que vamos explicar todos esses conceitos iniciais de uma maneira simples com o exemplo prático a seguir.
Calculando a cointegração entre dois ativos
Vamos começar importando as bibliotecas que estão faltando para usar no nosso exemplo. Adicionamos uma biblioteca para o cálculo da regressão linear (sklearn) e uma biblioteca de análise estatística chamada adfuller (vamos explicá-la em instantes).
%%capture
from sklearn.linear_model import LinearRegression
from statsmodels.tsa.stattools import adfuller
!pip install yfinance
import yfinance as yfComo nessa estratégia nós buscamos a relação entre dois ativos, vamos escolher as ações ordinárias e preferencial da Petrobras, PETR3 e PETR4. Contudo, essa estratégia por ser testada com qualquer par.
start_date = "2018-02-27"
end_date = "2019-03-02"
stock1 = "PETR3.SA"
stock2 = "PETR4.SA"
df = yf.download([stock1, stock2], start = start_date, end = end_date)["Adj Close"]
df.columns=['PETR3','PETR4']
df
[*********************100%***********************] 2 of 2 completed
| PETR3 | PETR4 | |
|---|---|---|
| Date | ||
| 2018-02-27 | 20.966679 | 19.296848 |
| 2018-02-28 | 20.993887 | 19.260950 |
| 2018-03-01 | 20.649277 | 18.875013 |
| 2018-03-02 | 21.021090 | 19.305826 |
| 2018-03-05 | 21.619623 | 19.853317 |
| ... | ... | ... |
| 2019-02-25 | 27.929766 | 24.999256 |
| 2019-02-26 | 27.938923 | 24.886902 |
| 2019-02-27 | 28.085442 | 25.355051 |
| 2019-02-28 | 27.343700 | 25.336321 |
| 2019-03-01 | 26.739319 | 24.999256 |
250 rows × 2 columns
Vamos agora plotar os pares junto com as médias para visualmente analisarmos se existe alguma relação entre eles e se os dados em si são estacionários no tempo.
mean_PETR3 = df['PETR3'].mean()
mean_PETR4 = df['PETR4'].mean()
df[['PETR3', 'PETR4']].plot(linewidth=1)
plt.axhline(y=mean_PETR3, color='#49ce8b', linestyle='--', linewidth=0.5)
plt.axhline(y=mean_PETR4, color='#033660', linestyle='--', linewidth=0.5)
plt.title("PETR3 & PETR4")Text(0.5, 1.0, 'PETR3 & PETR4')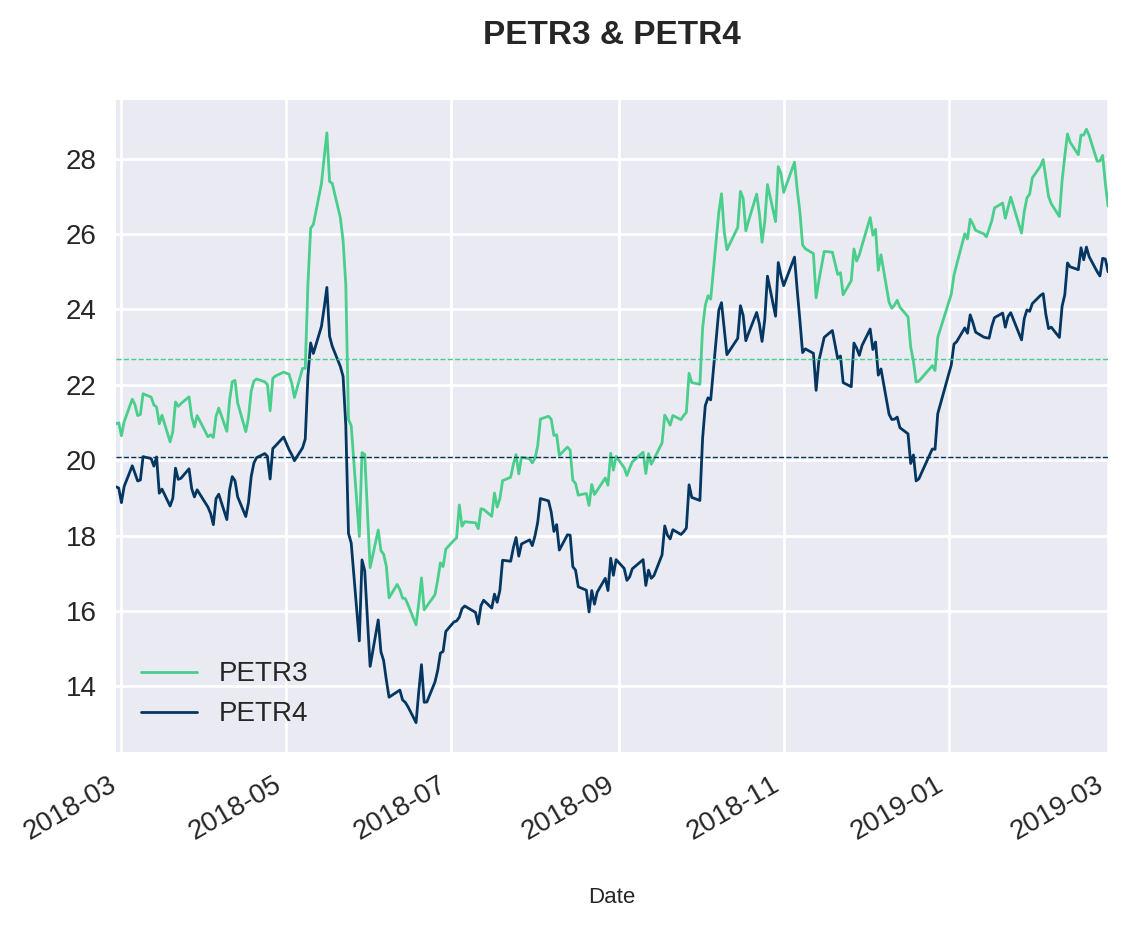
Como era de se esperar, os dados variam fortemente com o tempo. As séries não giram em torno da média (linha pontilhada). Não existe nenhum tipo de estacionaridade neles. Contudo, a visualização sugere que existe uma relação entre os pares: quando um sobe, o outro sobe junto e quando um cai, o outro também cai.
Método da Correlação
Para fortalecer o que acabamos de ver qualitativamente, vamos quantificar essa relação calculando a correlação entre os ativos. Lembre-se que a correlação varia entre -1 e 1.
Quando a correlação é igua a 1, os ativos variam da mesma maneira: quando um cai, o outro cai, quando um sobe, o outro sobe. Por outro lado, quando a correlação é igual a -1, os ativos se comportam de maneiras opostas: quando um cai o outro sobe.
A correlação pode ser facilmente calculada usando o método corr.
# Correlation
df.corr()| PETR3 | PETR4 | |
|---|---|---|
| PETR3 | 1.000000 | 0.989442 |
| PETR4 | 0.989442 | 1.000000 |
Nesse exemplo, vemos que existe uma alta correlação entre os ativos da Petrobras no período de tempo que escolhemos para análise. Se fossemos seguir uma estratégia baseado apenas na correlação, esse resultado estaria nos dizendo para prosseguir com a operação.
Porém, como vimos anteriormente, a correlação de pares não-estacionários na verdade varia com o tempo. Nesse sentido, essa correlação pode deixar de ser verdadeira em um próximo período. Por isso, vamos aprender a calcular se esses ativos estão na verdade cointegrados.
Método da Cointegração
O método da cointegração pode ser dividido em três partes:
- Ajustar um modelo linear ao nosso conjunto de dados;
- Calcular o resíduo entre o modelo e os valores reais;
- Procurar por estacionariedade no resíduo.
Vamos começar plotando os pares igual fizemos na nossa análise para calcular o beta entre dois ativos.
plt.scatter(df['PETR4'], df['PETR3'], s=5)
plt.xlabel("PETR4")
plt.ylabel("PETR3")
plt.show()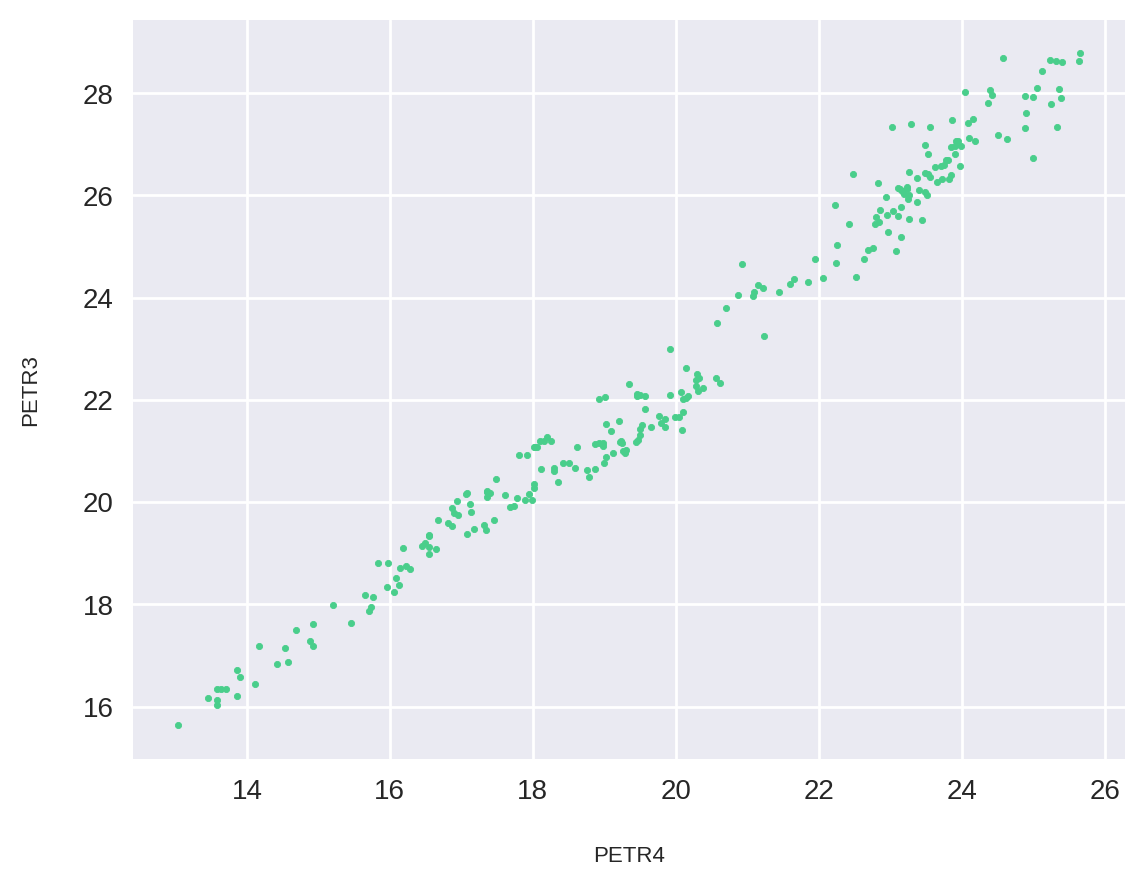
Seguindo o post de como calcular o beta entre dois ativos, vamos agora calcular uma regressão linear para acharmos a melhor reta que aproxima globalmente o comportamento da PETR3 com a PETR4. Ou seja, vamos achar uma função que, para cada valor de PETR4, vai tentar estimar o valor de PETR3.
O output da regressão linear nos dará os coeficientes da reta que melhor aproxima os nossos dados. Vamos armazenar essa nossa função numa variável chamada Y_predict. Note que para a variável independente (X_independent) estamos escolhendo a posição de index 1 no dataframe (PETR4), e para variável dependente (Y_dependent) estamos escolhendo a posição de index 0 (PETR3).
# Linear regression
# values converted into a numpy array
X_independent = df.iloc[:,1].values.reshape(-1, 1)
Y_dependent = df.iloc[:,0].values.reshape(-1, 1)
reg = LinearRegression().fit(X_independent, Y_dependent)
# get beta (angular coef of the linear regression)
beta = reg.coef_;
print('beta = %f' % beta)
# get b coef from (beta*x + b) of the linear regression)
b = reg.intercept_;
print('b = %f' % b)
# get the estimated Y values given X from the model
Y_predict = reg.predict(X_independent);beta = 1.044918
b = 1.692031
Até aqui nenhuma grande novidade pra quem leu o artigo sobre o beta. Em análises de cointegração, o beta ainda possui um papel muito importante. Ele nos dirá a proporção que devemos ficar comprados ou vendidos no pares. Mas isso será abordado com mais calma nos próximos posts da série, quando iremos focar na estratégia em si.
Vamos agora plotar nosso modelo linear junto com nossos dados.
plt.scatter(X_independent, Y_dependent, s=5)
plt.plot(X_independent, Y_predict, color="red", label='Linear Model')
plt.xlabel("PETR4")
plt.ylabel("PETR3")
plt.legend()
plt.show()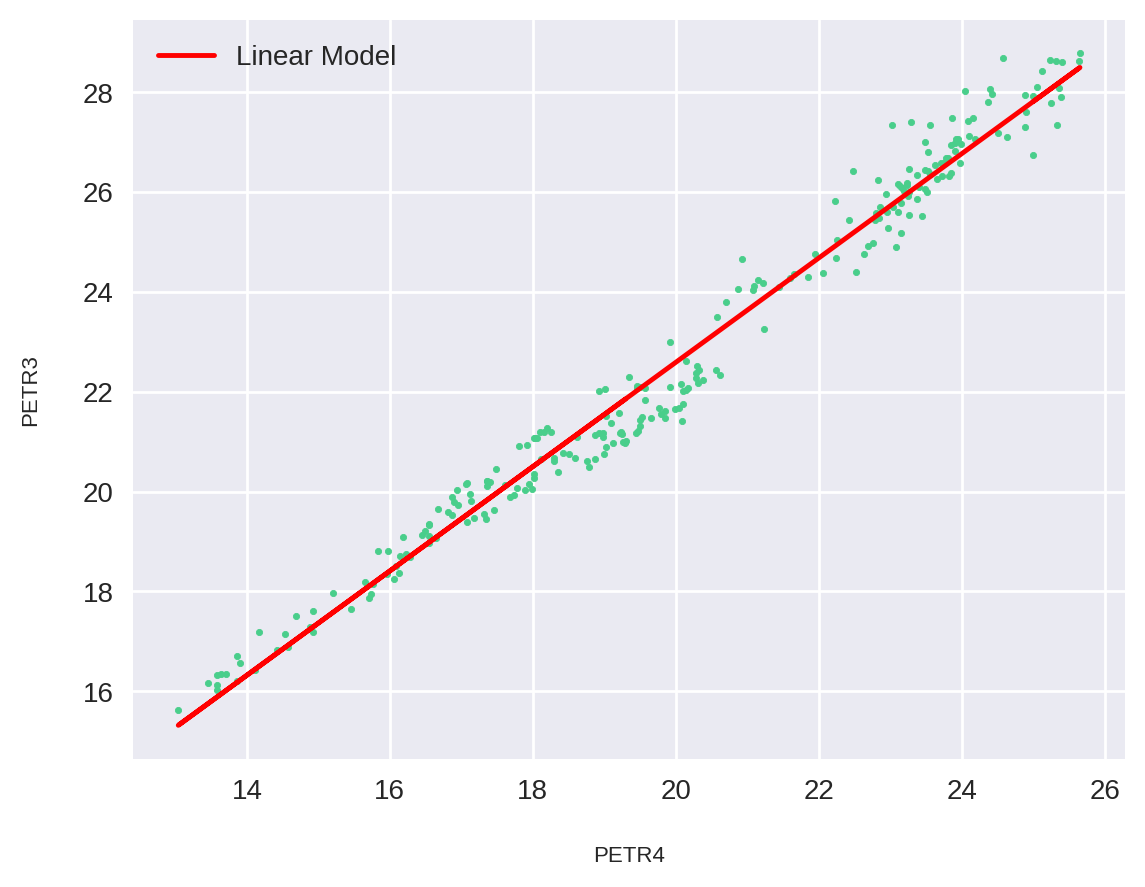
Como podemos ver, alguns pontos pertencem exatamente ao nosso modelo linear, embora a maioria esteja ligeiramente afastada.
O segundo passo é calcularmos o resíduo. Agora que temos o valor previsto de Y, o resíduo (ou erro) pode ser calculado como a diferença entre o ponto previsto (calculado pelo nosso modelo linear) e o ponto observado (o valor observado na realidade).
O resíduo pode ser facilmente calculado em Python subtraindo Y_predict de Y_dependent.
df['Residual'] = Y_dependent - Y_predict
df
| PETR3 | PETR4 | Residual | |
|---|---|---|---|
| Date | |||
| 2018-02-27 | 20.966679 | 19.296848 | -0.888983 |
| 2018-02-28 | 20.993887 | 19.260950 | -0.824264 |
| 2018-03-01 | 20.649277 | 18.875013 | -0.765602 |
| 2018-03-02 | 21.021090 | 19.305826 | -0.843953 |
| 2018-03-05 | 21.619623 | 19.853317 | -0.817503 |
| ... | ... | ... | ... |
| 2019-02-25 | 27.929766 | 24.999256 | 0.115553 |
| 2019-02-26 | 27.938923 | 24.886902 | 0.242112 |
| 2019-02-27 | 28.085442 | 25.355051 | -0.100547 |
| 2019-02-28 | 27.343700 | 25.336321 | -0.822717 |
| 2019-03-01 | 26.739319 | 24.999256 | -1.074894 |
250 rows × 3 columns
Agora podemos plotar esse resíduo para checarmos primeiramente se eles são graficamente estacionários. Ou seja, precisamos ver se a média e o desvio padrão do resíduo são constantes.
Para essa visualização, vamos deslocar o desvio padrão em vezes da média, para cima e para baixo, para vermos se o resíduo está comportado dentro desse espaço. Normalmente, o valor utilizado para o deslocamento do desvio padrão é .
mean = df['Residual'].mean()
std = df['Residual'].std()
k = 2 # Factor to shift the standard deviation
up = mean + std * k
down = mean - std * k
plt.title("Residual")
df['Residual'].plot(x="Major", y="", label='_nolegend_')
plt.axhline(y=mean, color='y', linestyle='--', linewidth=1, label='Mean')
plt.axhline(y=up, color='b', linestyle='--', linewidth=1, label=f'+/-{k} STD')
plt.axhline(y=down, color='b', linestyle='--', linewidth=1, label='_nolegend_')
plt.legend(loc='upper right',ncol=2)<matplotlib.legend.Legend at 0x7fb0217f6f90>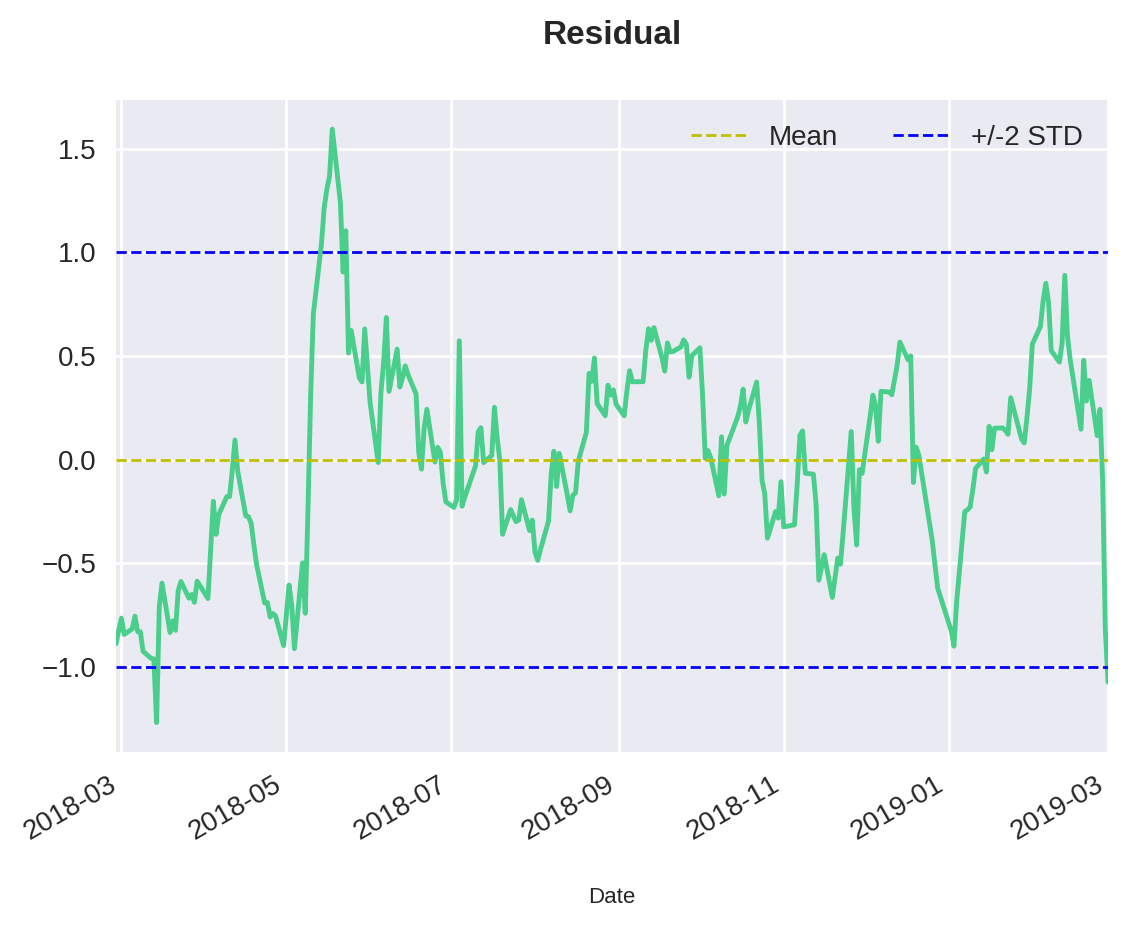
De fato, parece que o resíduo, diferentemente do comportamento dos ativos, oscila em relação à sua média, entre duas vezes o desvio padrão para cima e para baixo. Como vimos, esse é um dos indicativos de que o resíduo pode ser estacionário. Contudo, alguns podem argumentar que não veem esse resíduo perfeitamente estacionário. E, obviamente, nós tentamos evitar ao máximo critérios subjetivos na análise quantitativa.
Sendo assim, vamos primeiramente dividir essa série na metade e calcular a média e a variância de cada uma. Quanto mais esses valores se aproximarem, maiores as chances de termos uma série estacionária.
Para fazermos isso, vamos achar o meio da série pegando o inteiro da divisão por dois e usar os métodos mean e var para calcularmos a média e a variância, respectivamente.
split = int(len(df.Residual) / 2)
S1, S2 = df.Residual[0:split], df.Residual[split:]
mean1, mean2 = S1.mean(), S2.mean()
var1, var2 = S1.var(), S2.var()
print('mean1=%f, mean2=%f' % (mean1, mean2))
print('variance1=%f, variance2=%f' % (var1, var2))mean1=-0.123304, mean2=0.123304
variance1=0.321860, variance2=0.152735
Nesse exemplo as médias possuem o mesmo valor absoluto e as variâncias estão na mesma ordem de magnitude, o que sugere que a série pode de fato ser estacionária.
O teste de Dickey-Fuller
Existem métodos mais robustos de análise estatística que determinam se uma série é estacionária ou não com uma porcentagem de confiabilidade. Usualmente o teste mais utilizado se chama Augmented Dickey-Fuller.
Simplificadamente, esse teste busca identificar a presença de uma raiz unitária na série. A maioria dos dados do mercado financeiro possui uma raiz unitária, pois ela é uma característica dos processos que evoluem ao longo do tempo. Contudo, se o teste de Dickey-Fuller rejeitar a hipótese da existência de uma raiz unitária, há a possibilidade dela ser estacionária.
Além disso, o teste nos retorna o famoso p-value, que basicamente determina a probabilidade do resultado ter sido encontrado por mero acaso.
O teste Augmented Dickey-Fuller pode então ser chamado usando a função adfuller da biblioteca statsmodels.tsa.stattools, que já importamos lá no começo do nosso código. Ela recebe a nossa série (nesse caso o resíduo) e retorna os valores desejados.
test_series = adfuller(df['Residual'])
print('ADF Statistic: %f' % test_series[0])
print('p-value: %f' % test_series[1])
print('Critical values:')
for key, value in test_series[4].items():
print('\t%s: %.3f' % (key, value))
confidence = 1 - test_series[1]
print(f'Confidence: {confidence:.2%}') ADF Statistic: -3.839773
p-value: 0.002526
Critical values:
1%: -3.457
5%: -2.873
10%: -2.573
Confidence: 99.75%
O primeiro output é o valor do teste estatístico, -3.8397. Para o teste de estacionariedade, quanto mais negativo esse resultado, maiores as chances da série ser estacionária. O p-value calculado para essa série é de 0.002526, que podemos usar para calcularmos a confiabilidade em porcentagem pela fórmula:
No nosso exemplo, a confiabilidade é de 99.75%. Como geralmente valores acima de 95% já são suficientes para análise, o resultado então nos confirma que os ativos estão cointegrados com 99.75% de confiabilidade.
Considerações finais
Na primeira parte dessa série, aprendemos como calcular o fundamento básico para a estrátegia de Long & Short por cointegração: o teste da estacionariedade do resíduo.
Após começarmos com um simples exemplo para entendermos o conceito de estacionaridade de uma série, partimos para um exemplo real prático, onde o par PETR3 e PETR4 foi escolhido. Após isso, relembramos como calcular o beta entre os dois ativos e aprendemos como usar o nosso modelo linear para calcularmos o resíduo. Finalmente, aprendemos como interpretar os resultados do teste Augmented Dickey-Fuller, onde definimos uma confiabilidade mínima de 95% no teste para que possamos aceitar a nossa série como estacionária.
Durante a leitura desse artigo, você pode ter se perguntado:
"Quando você importou os dados, você escolheu 250 dias. E se eu escolhesse menos? Ou mais? Teria alguma diferença?"
"E onde entra o beta? Como usar isso para fazer um trade?"
Tudo isso e muito mais será explicado em detalhes nos próximos artigos, quando começaremos a aplicar a estratégia em si. Mas vocês podem brincar em mudar o intervalo de tempo e conferir se a cointegração permanece válida.
Até agora, esperamos que vocês tenham entendido esses fundamentos iniciais que serão a chave para prosseguirmos com nossas análises. Por isso, não se esqueçam de se inscrever no nosso site e no grupo do Telegram para se manterem atualizados com a sequência do artigo.
Um grande abraço e até a próxima!
Inscreva-se no canal do QuantBrasil!
Acompanhe novidades sobre a plataforma, vídeos sobre finanças quantitativas, tutoriais sobre programação e Inteligência Artificial!