Entenda o que é o Beta e Aprenda a Calculá-lo Utilizando Python
Assista também no YouTube
É muito comum, durante a montagem de um portfólio, nos depararmos com o termo beta de um ativo ou beta da carteira. O beta é um número que tem como objetivo nos dar uma medida do risco daquele ativo ou portfólio.
No artigo de hoje nós vamos entender a fundo o que é o beta, sua aplicabilidade e limitações, além de calculá-lo de três formas diferentes.
O que é o beta?
De forma simplificada, o beta mede a expectativa de quanto um ativo se moverá em relação a um outro ativo subjacente. É comum que o ativo subjacente seja um benchmark, como por exemplo o IBOV para ativos brasileiros ou o SPX no mercado americano.
Portanto, se um ativo possui , podemos esperar que pra cada 1% que o ativo subjacente se mova, andará 1.5%. Analogamente, se o beta do ativo é , então a expectativa é que terá movimentos com 80% da magnitude que o ativo subjacente.
O beta é a base do Capital Asset Princing Model, um modelo que busca descrever a relação entre risco sistemático de um investimento com o seu retorno esperado.
Qual a importância do beta de um ativo?
A grande vantagem do cálculo de um beta diz respeito à volatilidade que um investidor deve esperar para aquele ativo. Ativos com beta maior que 1 tendem a apresentar volatilidade maior que o mercado, enquanto ativos com beta menor que 1 tendem a apresentar volatilidade menor que o mercado. Para conferir o beta e a volatilidade dos ativos do Ibovespa, clique aqui.
Dessa forma, na hora da montagem de um portfólio ou na escolha de uma ação, é prudente levar o cálculo do beta em consideração para não ser pego de surpresa. Em momentos risk on, quando o mercado está positivo e direcional, pode ser interessante adicionar ativos de maior beta na carteira, enquanto em momentos de incerteza e proteção, ativos de beta menor tendem a "defender" seu patrimônio.
Por último, assim como o drawdown, o beta é extremamente importante em momentos de alavancagem, onde o investidor precisa identificar a volatilidade estimada de seu portfólio para evitar quebrar a conta em momentos de movimentação intensa.
O que é o coeficiente beta de uma carteira?
O beta pode ser calculado para ativos ou grupos de ativos. Nesse caso, o beta de um portfólio pode ser encontrado ponderando o beta de cada ativo pelo seu peso na carteira.
Ou seja, se um portfólio é composto em 60% pelo ativo cujo beta é igual a e em 40% pelo ativo cujo beta é igual a :
Esse resultado pode ser interpretado como uma medida de risco da carteira. Como a carteira assume 22% mais risco que o benchmark, é esperado um retorno maior ao final de um horizonte de investimento adequado.
Como calcular o beta?
Existem três formas principais para se calcular o beta de um ativo:
Método 1
A primeira forma é a seguinte:
Onde é o ativo que queremos calcular o beta, é o benchmark, é a variância do benchmark e é a covariância entre e .
Explicar cada um desses conceitos de estatística está fora do escopo desse artigo, porém é importante sua familiaridade ao se aprofundar nas análises quantitativas.
Método 2
A segunda forma, e provavelmente a mais fácil de entender, define o beta como a razão do desvio padrão de dois ativos multiplicada pela sua correlação. Matematicamente:
Onde é a correlação entre os ativos e e é o desvio padrão.
Se entendermos o desvio padrão como a volatilidade de um ativo, então o beta é definido como a razão entre as volatilidades ponderada pela correlação.
Método 3
Finalmente, a terceira forma de entender o beta e a matematicamente mais elaborada, é como o coeficiente angular da regressão linear entre das variações dos ativos.
Apesar de mais elaborada, a regressão linear é importante principalmente para estudos futuros de cointegração e Machine Learning. De forma simplificada, a regressão linear busca achar a "melhor reta" que descreve a relação entre dois conjuntos de pontos (nesse caso, as variações de preço dos papeis). Uma vez achada essa reta, o coeficiente angular pode ser entendido como a abertura (angulação) da reta em relação ao eixo X.
A seguir nós vamos aprender a calcular o beta das três formas descritas acima.
Baixando as bibliotecas
O primeiro passo é importar as bibliotecas que serão utilizadas no cálculo e visualização do beta. Repare que estamos introduzindo a função LinearRegression da famosa biblioteca sci-kit learn (sklearn). Como você pode imaginar, ela será utilizada para calcular o beta utilizando o método da regressão linear.
%%capture
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
!pip install yfinance
import yfinance as yf
from sklearn.linear_model import LinearRegressionCom as bibliotecas importadas nós podemos baixar os dados do ativo que queremos calcular o beta e seu respectivo benchmark. Para esse exemplo, usaremos a VALE3, cujo benchmark é o índice Bovespa (BVSP). O período de cálculo será entre 2016 e 2020 (5 anos) e desconsideraremos valores nulos por simplicidade.
start_date = "2016-01-01"
end_date = "2020-12-31"
bench_name = "^BVSP"
asset_name = "VALE3.SA"
df = yf.download([asset_name, bench_name], start = start_date, end = end_date)["Adj Close"]
df.columns=['Asset','Benchmark'];
df.dropna(inplace=True)
df
| Asset | Benchmark | |
|---|---|---|
| Date | ||
| 2016-01-04 | 10.387794 | 42141.0 |
| 2016-01-05 | 10.248634 | 42419.0 |
| 2016-01-06 | 9.495541 | 41773.0 |
| 2016-01-07 | 8.930719 | 40695.0 |
| 2016-01-08 | 8.627845 | 40612.0 |
| ... | ... | ... |
| 2020-12-22 | 83.192207 | 116348.0 |
| 2020-12-23 | 83.594101 | 117857.0 |
| 2020-12-28 | 83.546249 | 119051.0 |
| 2020-12-29 | 83.316597 | 119475.0 |
| 2020-12-30 | 83.680214 | 119306.0 |
1236 rows × 2 columns
Repare que o cálculo do beta leva em consideração a variação percentual. Podemos rapidamente calculá-la utilizando a função pct_change(). Como o primeiro valor será NaN, podemos aproveitar para desconsiderá-lo também.
df["% Benchmark"] = df["Benchmark"].pct_change()
df["% Asset"] = df["Asset"].pct_change()
df = df[1:]
df
| Asset | Benchmark | % Benchmark | % Asset | |
|---|---|---|---|---|
| Date | ||||
| 2016-01-05 | 10.248634 | 42419.0 | 0.006597 | -0.013396 |
| 2016-01-06 | 9.495541 | 41773.0 | -0.015229 | -0.073482 |
| 2016-01-07 | 8.930719 | 40695.0 | -0.025806 | -0.059483 |
| 2016-01-08 | 8.627845 | 40612.0 | -0.002040 | -0.033914 |
| 2016-01-11 | 8.382270 | 39950.0 | -0.016301 | -0.028463 |
| ... | ... | ... | ... | ... |
| 2020-12-22 | 83.192207 | 116348.0 | 0.002862 | 0.000921 |
| 2020-12-23 | 83.594101 | 117857.0 | 0.012970 | 0.004831 |
| 2020-12-28 | 83.546249 | 119051.0 | 0.010131 | -0.000572 |
| 2020-12-29 | 83.316597 | 119475.0 | 0.003561 | -0.002749 |
| 2020-12-30 | 83.680214 | 119306.0 | -0.001415 | 0.004364 |
1235 rows × 4 columns
A primeira fórmula de cálculo apresentada foi a da covariância dividida pela variância do benchmark. Assim, em uma linha de código, podemos calcular o beta de VALE3 de 2016 a 2020:
beta_1 = df["% Asset"].cov(df["% Benchmark"]) / df["% Benchmark"].var()
beta_1
1.071940480747427
Como o beta da VALE3 foi maior que 1, podemos interpretar essa ação como mais volátil que o Ibovespa. No caso, para cada variação de 1% no benchmark a Vale é esperada de variar 1.07%.
A segunda forma tradicional de cálculo do beta é atráves das razões dos desvio padrão multiplicadas pela correlação. As funções corr() e std() são tudo que precisamos:
std_asset = df["% Asset"].std()
std_bench = df["% Benchmark"].std()
corr = df["% Asset"].corr(df["% Benchmark"])
beta_2 = corr * (std_asset / std_bench)
beta_2
1.0719404807474269
Como esperado, o valor do beta encontrado é o mesmo do passo anterior.
Calculando o beta através da regressão linear
Agora que já calculamos o beta estamos preparados para o realizar a regressão linear. O primeiro passo é colocar nossos dados, no caso a variação percentual de cada ativo, no formato necessário.
Faremos isso através da função reshape(), que nos permite transformar a nossa série de dados em um array unidimensional de linhas.
Vamos entender melhor o formato da nossa série de dados:
X = df["% Benchmark"]
print("Type of X: ", type(X))
print("Shape of X:", X.shape)Type of X: <class 'pandas.core.series.Series'> Shape of X: (1235,)
Repare que df["% Benchmark"] é um objeto da classe Series com 1235 valores. Nós podemos transformá-lo num array utilizando o método .values:
X = X.values
print("Type of X: ", type(X))
print("Shape of X:", X.shape)
X
Type of X: <class 'numpy.ndarray'> Shape of X: (1235,)
array([ 0.0065969 , -0.01522902, -0.02580614, ..., 0.01013092, 0.0035615 , -0.00141452])Conseguimos transformar nossa série em um array, porém precisamos explicitar que ele é unidimensional. Para colocá-lo no formato final de nnn linhas e 1 coluna, utilizaremos o método reshape(row, columns). Como queremos apenas uma coluna mas o número de linhas pode variar, passaremos como parâmetro a tupla (-1, 1) (leia a seguinte discussão para mais detalhes).
X = df["% Benchmark"].values.reshape(-1, 1)
print("Type of X: ", type(X))
print("Shape of X:", X.shape)
X
Type of X: <class 'numpy.ndarray'> Shape of X: (1235, 1)
array([[ 0.0065969 ], [-0.01522902], [-0.02580614], ..., [ 0.01013092], [ 0.0035615 ], [-0.00141452]])Pronto! O processo acima pode ser rapidamente feito para os dois ativos da seguinte forma:
X = df["% Benchmark"].values.reshape(-1, 1)
Y = df["% Asset"].values.reshape(-1, 1)
plt.scatter(X, Y, s=3)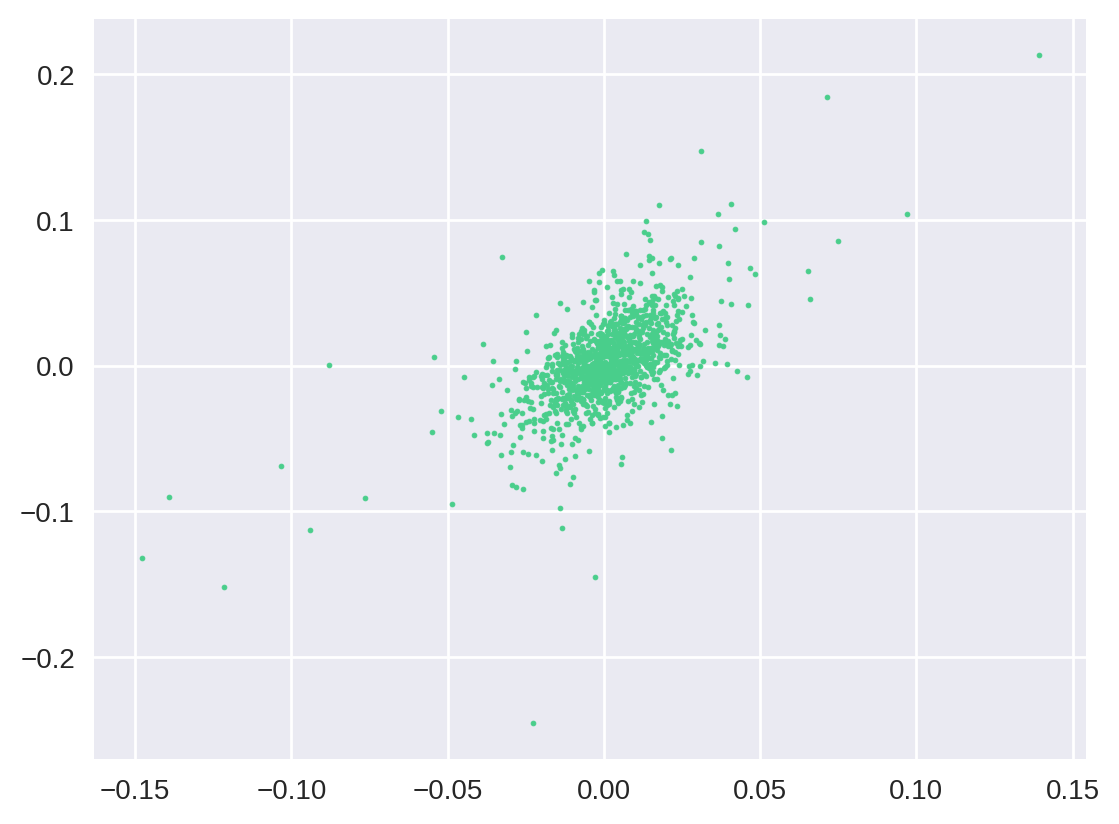
O gráfico acima é um scatter plot e descreve como as variações entre X e Y se relacionam. Para cada variação de preço no eixo X (IBOV), nós achamos a variação de Vale no mesmo dia (eixo Y) e marcamos o ponto no gráfico.
Observe que a escolha dos eixos importa. Se queremos calcular o beta de em relação a , então as variações percentuais de preço de devem estar no eixo X e as de no eixo Y.
A regressão linear dos dois ativos é a reta que melhor se aproxima de todos os pontos, ou seja, a reta que tem minimiza o erro entre o ponto observado e a reta prevista.
Vamos usar o LinearRegression para achar a reta:
# Find best line
linear_regressor = LinearRegression()
reg = linear_regressor.fit(X, Y)
# Predict Y values from line found
Y_pred = linear_regressor.predict(X)
# Plot scatter along with regression
plt.scatter(X, Y, s=3)
plt.plot(X, Y_pred, color='red')
plt.show()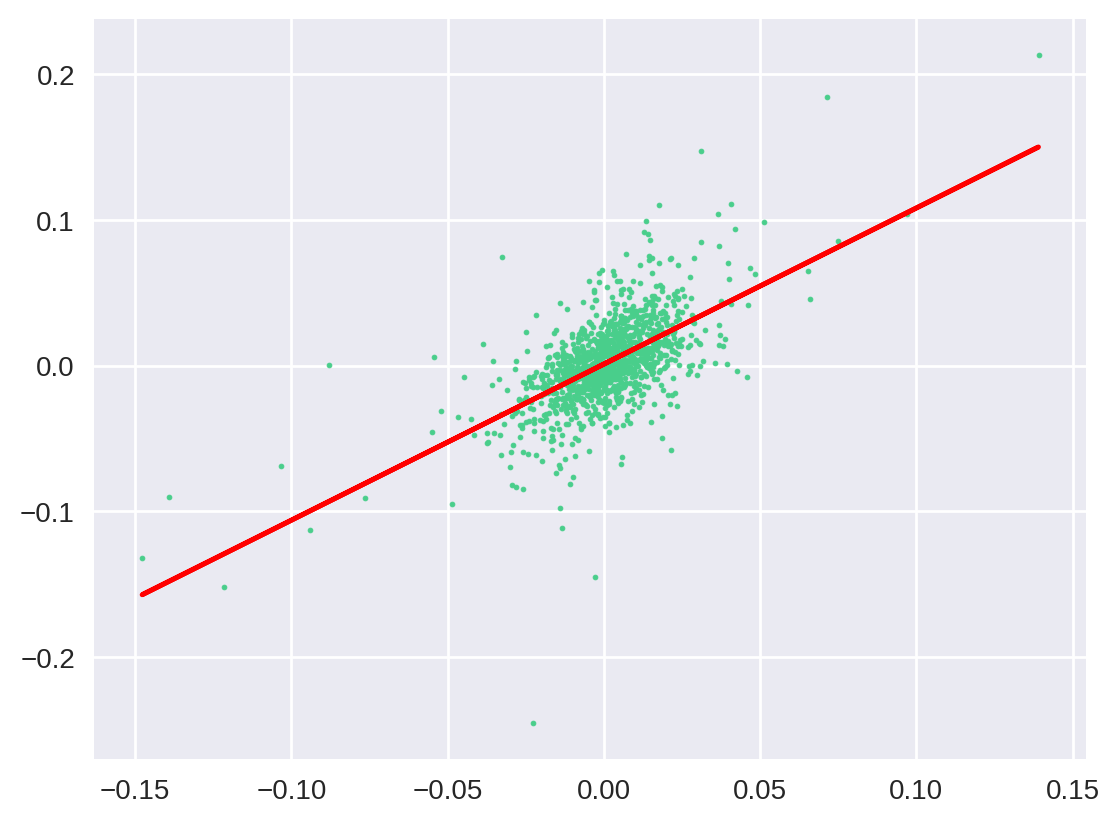
E aí está! Repare que a reta vermelha tenta melhor descrever o relacionamento entre os pontos verdes. O beta, ou coeficiente angular, é a angulação da reta e o mesmo valor encontrado anteriormente:
beta_3 = reg.coef_[0][0]
beta_3
1.0719404807474275
Limitações do beta
Impacto do tempo
O beta é fortemente dependente da janela de tempo e timeframe escolhidos, o que significa que ativos podem apresentar betas diferentes ao longo de suas vidas. Por isso é importante acompanhar seus investimentos de perto e conferir se você não está "desenquadrado" com o risco máximo que pretende assumir.
A melhor escolha de timeframe é objeto de estudos (como esse e esse) e pode variar de acordo com seu objetivo. De modo geral, principalmente pela maior abundância de dados, analisar retornos diários em vez de mensais ou semanais pode ser a melhor opção.
Riscos de cauda (tail risk)
Por assumir que a variação percentual dos ativos obedece a uma curva normal (na prática isso não é verdade), o beta não provém segurança contra riscos de cauda (os famosos black swans). Portanto, um investidor pode ter a falsa segurança de que está protegido ao operar alavancado e ser surpreendido por uma movimentação alguns desvio padrão acima do previsto.
Conclusão
O beta é uma métrica relevante de risco para investimentos. Felizmente, podemos calculá-lo com algumas poucas linhas de código.
O cálculo da regressão linear é um pouco mais trabalhoso, mas é importante entender sua intepretação já que ela é bastante utilizada em métodos quantitativos como cointegração (que será explorada em futuros posts).
Conferindo o valor do beta
O famoso site Investing.com utiliza uma regressão linear de 60 meses para cálculo do beta, o que significa que eles não disponibilizam o beta de ativos que entraram há menos tempo da bolsa, como BIDI4, e que os valores lá apresentados podem diferir bastante de betas calculados em cima de retornos diários mais recentes.
A boa notícia é que os usuários do QuantBrasil podem calcular o beta de qualquer ação através do nosso bot no Telegram! Além disso, o beta dos ativos do Ibovespa nos últimos 365 dias podem ser conferidos diretamente no site.
Inscreva-se no canal do QuantBrasil!
Acompanhe novidades sobre a plataforma, vídeos sobre finanças quantitativas, tutoriais sobre programação e Inteligência Artificial!