O ano de 2022 está chegando ao fim e com ele vêm as expectativas e projeções para o novo ano. E nós, claro, não poderíamos deixar passar essa oportunidade de aplicar métodos quantitativos e estatísticos para responder o que todos querem saber: pra onde vai o IBOV em 2023?
Para responder essa pergunta, vamos utilizar uma combinação de duas abordagens quantitativas:
- Projetar zonas de suporte e resistência utilizando a volatilidade de 2022;
- Rodar uma simulação de Monte Carlo para calcular intervalos de confiança para o preço ao final de 2023 utilizando as mesmas propriedades estatísticas de 2022.
Mãos à obra!
Projetando Zonas de Suporte e Resistência
Para gerar as zonas de suporte e resistência para 2023, irei me basear no paper Supply and Demand Levels Forecasting Based on Returns Volatility, do meu amigo Leandro Guerra, criador do Outspoken Market.
De forma simplificada, na abordagem proposta pelo Leandro nós geramos os retornos de um ativo no corrente ano e calculamos o desvio-padrão de uma janela móvel de
Curioso para ver as zonas de suporte e resistência na prática? Nós disponibilizamos uma ferramenta onde você pode gerá-las, para qualquer ativo, de graça. Confere lá!
Dito isso, vamos ao código.
Baixando os dados do IBOV em 2022
A primeira coisa que precisamos, naturalmente, é dos dados relativos aos preços do Ibovespa em 2022. Por sorte, esses dados são facilmente encontrados na internet, por exemplo no Stooq.
Baixe os dados diários e importe-os em um DataFrame:
import pandas as pd
import numpy as np
df = pd.read_csv('../data/ibov_2022.csv', index_col='Date', parse_dates=True)
df
| Open | High | Low | Close | Volume | |
|---|---|---|---|---|---|
| Date | |||||
| 2022-01-03 | 104823.40 | 106125.50 | 103413.40 | 103921.60 | 1.127626e+09 |
| 2022-01-04 | 103921.60 | 104276.30 | 103096.30 | 103513.60 | 1.149161e+09 |
| 2022-01-05 | 103513.60 | 103513.60 | 100849.60 | 101005.60 | 1.288369e+09 |
| 2022-01-06 | 101005.80 | 102234.70 | 100999.90 | 101561.10 | 1.174921e+09 |
| 2022-01-07 | 101561.10 | 102719.50 | 101104.00 | 102719.50 | 1.173341e+09 |
| ... | ... | ... | ... | ... | ... |
| 2022-12-23 | 107551.70 | 109994.23 | 107551.70 | 109697.57 | 1.284711e+09 |
| 2022-12-26 | 109698.84 | 109755.23 | 108308.77 | 108737.75 | 5.219539e+08 |
| 2022-12-27 | 108739.34 | 109352.67 | 107418.40 | 108578.20 | 1.115808e+09 |
| 2022-12-28 | 108578.38 | 110535.56 | 108578.38 | 110236.71 | 1.119396e+09 |
| 2022-12-29 | 110237.41 | 111177.50 | 109560.30 | 109734.60 | NaN |
250 rows × 5 columns
Calculando a Volatilidade
De posse dos dados, já podemos calcular os retornos e a volatilidade no ano:
df["Returns"] = df['Close'].pct_change()
# Rolling window period
period = 20
# Approximate number of data points in an year
trading_days = 250
df["Vol"] = np.round(df["Returns"].rolling(period).std() * np.sqrt(trading_days), 4)
df
| Open | High | Low | Close | Volume | Returns | Vol | |
|---|---|---|---|---|---|---|---|
| Date | |||||||
| 2022-01-03 | 104823.40 | 106125.50 | 103413.40 | 103921.60 | 1.127626e+09 | NaN | NaN |
| 2022-01-04 | 103921.60 | 104276.30 | 103096.30 | 103513.60 | 1.149161e+09 | -0.003926 | NaN |
| 2022-01-05 | 103513.60 | 103513.60 | 100849.60 | 101005.60 | 1.288369e+09 | -0.024229 | NaN |
| 2022-01-06 | 101005.80 | 102234.70 | 100999.90 | 101561.10 | 1.174921e+09 | 0.005500 | NaN |
| 2022-01-07 | 101561.10 | 102719.50 | 101104.00 | 102719.50 | 1.173341e+09 | 0.011406 | NaN |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 2022-12-23 | 107551.70 | 109994.23 | 107551.70 | 109697.57 | 1.284711e+09 | 0.019954 | 0.2224 |
| 2022-12-26 | 109698.84 | 109755.23 | 108308.77 | 108737.75 | 5.219539e+08 | -0.008750 | 0.2247 |
| 2022-12-27 | 108739.34 | 109352.67 | 107418.40 | 108578.20 | 1.115808e+09 | -0.001467 | 0.2126 |
| 2022-12-28 | 108578.38 | 110535.56 | 108578.38 | 110236.71 | 1.119396e+09 | 0.015275 | 0.2137 |
| 2022-12-29 | 110237.41 | 111177.50 | 109560.30 | 109734.60 | NaN | -0.004555 | 0.2087 |
250 rows × 7 columns
Nada de novo por aqui se você já acompanha nosso blog. De forma simplificada, traduzimos o que explicamos na seção anterior em código. Repare que assumimos uma janela móvel de 20 dias, valor que pode ser alterado a gosto (disponível para assinantes Premium no nosso Simulador de Suportes e Resistências).
Vamos agora utilizar a última volatilidade do ano para projetar as zonas de suporte e resistência:
# Let's isolate the yearly close
last_close = df['Close'][-1]
# The last volatility is the final volatility for the year
vol = df['Vol'][-1]
# Factors will be used to multiply the volatility and generate multiple zones
factors = [2, 1, -1, -2]
for factor in factors:
price_zone = round((1 + factor * vol) * last_close, 4)
print(f"Price zone {factor}σ: {price_zone}")Price zone 2σ: 155537.822
Price zone 1σ: 132636.211
Price zone -1σ: 86832.989
Price zone -2σ: 63931.378
E aí está: geramos as zonas de forma bem simples. Multiplicamos o valor de fechamento do ano por um múltiplo (fator) da última volatilidade observada. Podemos interpretar as zonas de preço da seguinte forma:
- 132k é a primeira resistência por volatilidade, e 155k a segunda;
- 86k é o primeiro suporte por volatilidade, e 63k o segundo.
Em outras palavras, podemos dizer que o IBOV deve transitar entre 86k e 132k (-1 e +1 desvio-padrão) com ~68% de chance, e entre 155k e 63k com 95% de chance. Em breve vamos analisar se esses números fazem sentido empíricamente.
Simulando Preços com Monte-Carlo
A primeira etapa do nosso estudo já foi. Agora, iremos complementá-lo com uma simulação de Monte-Carlo. Se você ainda não é familiar com o termo, recomendo a leitura do nosso artigo Como Criar uma Simulação de Monte Carlo no Mercado Financeiro Utilizando Python.
De forma resumida, para realizar uma simulação de Monte-Carlo precisamos gerar uma distribuição de retornos com as mesmas propriedades estatísticas observadas em 2022: média e desvio-padrão. Uma vez que essa distribuição esteja estabelecida, geramos retornos sintéticos (simulados) para os próximos 250 dias.
Vamos começar calculando as propriedades estatísticas do IBOV em 2022:
# Get the list of all returns, excluding the first value which is NaN
returns_list = df["Returns"].to_list()[1:]
# Compute mean and standar deviation
mean = np.mean(returns_list)
std_dev = np.std(returns_list)
print(f"Mean: {mean:.4%}")
print(f"Std: {std_dev:.4%}")Mean: 0.0306%
Std: 1.3241%
De posse das propriedades estatísticas, os próximos passos são muito simples. Primeiro, nós definiremos simulations como o número de simulações desejadas. Quanto maior esse número, mais fidedigno o resultado (até certo ponto).
Depois, para cada simulação nós geraremos um conjunto de retornos sintéticos observando as propriedades estatísticas calculadas. A composição desses retornos ao longo de mais 250 dias dará o valor final, projetado, do IBOV em 2023. Simples, não?
Para gerar os retornos sintéticos, utilizaremos a biblioteca scipy.stats.norm, que providencia diversos métodos estatísticos para a curva normal.
Em particular, estamos interessados na ppf, ou Percent Point Function, que retorna o valor da distribuição requerido para uma determinada probabilidade.
Ficou confuso? Vamos de novo. Se gerarmos uma curva normal com média e desvio-padrão específicos, podemos então gerar uma probabilidade aleatória (um valor entre 0 e 1), e descobrir qual valor, na distribuição, gera tal probabilidade. Para os versados em estatística, a ppf é a função inversa da cdf (Cumulative Distribution Function).
Vamos entender com código:
from scipy.stats import norm
mean = 0
std = 1
# Create curve with normal params
norm.cdf(0, loc=mean, scale=std)
0.5Numa distribuição normal com mean = 0 e std = 1, sabemos que metade dos valores estão após o 0 e metade depois do 0 (por isso 0 é a média.)
Ou seja, o valor da cdf é justamente esse: a probabilidade de que uma variável aleatória seja menor ou igual a um determinado valor na distribuição (nesse caso, 50%). O gráfico a seguir deixa tudo mais claro.
import matplotlib.pyplot as plt
num_points = 100
# Generate 100 points between the deviations
x = np.linspace(mean - 2 * std, mean + 2 * std, num_points)
# Plot the normal distribution
plt.plot(x, norm.pdf(x, mean, std))
# Plot the vertical line right at the mean
plt.plot([mean] * num_points, norm.pdf(x, mean, std))
plt.show()
Já a ppf é a função inversa, ou seja: qual valor corresponde a uma probabilidade de 50%? Como vimos anteriormente, para essa distribuição, esse valor é 0.
from scipy.stats import norm
norm.ppf(0.5)0.0Muito bem! Agora que já entendemos o que é uma ppf vamos ao código que gera retornos sintéticos e calcula o valor final de fechamento do IBOV em 2023. Primeiro vamos gerar a curva original:
# Generate list with all closes in the current year
# and the corresponding trading day
closes_list = df["Close"].to_list()
days = [i for i in range(1, len(df['Close']) + 1)]
# Plot closing prices
fig = plt.figure(figsize=(10, 4))
plt.plot(days, closes_list)[<matplotlib.lines.Line2D at 0x7fd7fa540390>]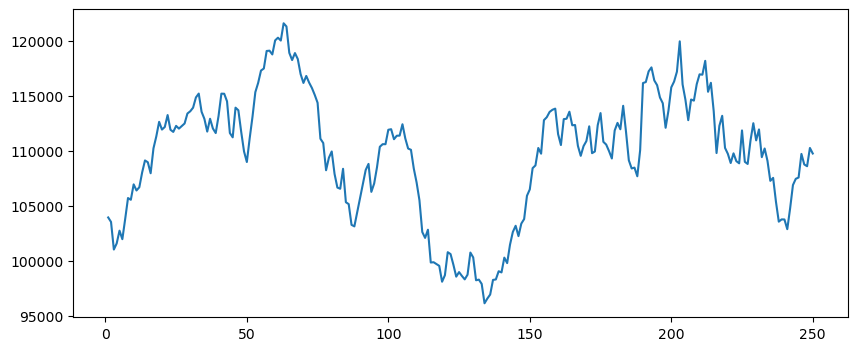
Agora podemos gerar nossa simulação:
from scipy.stats import norm
from random import random
# Plot closes again
fig = plt.figure(figsize=(12, 6))
plt.plot(days, closes_list)
# Number of simulations, i.e., curves that will be projected
simulations = 500
all_synthetic_closes = []
# Generate synthetic trading days
num_days = [days[-1]]
for i in range(trading_days):
num_days.append(num_days[-1] + 1)
for i in range(simulations):
closes = [last_close]
# Generate synthetic closes
for j in range(trading_days):
pct_change = norm.ppf(random(), loc=mean, scale=std_dev)
synthetic_close = closes[-1] * (1 + pct_change)
closes.append(synthetic_close)
last_synthetic_close = closes[-1]
all_synthetic_closes.append(last_synthetic_close)
plt.plot(num_days, closes)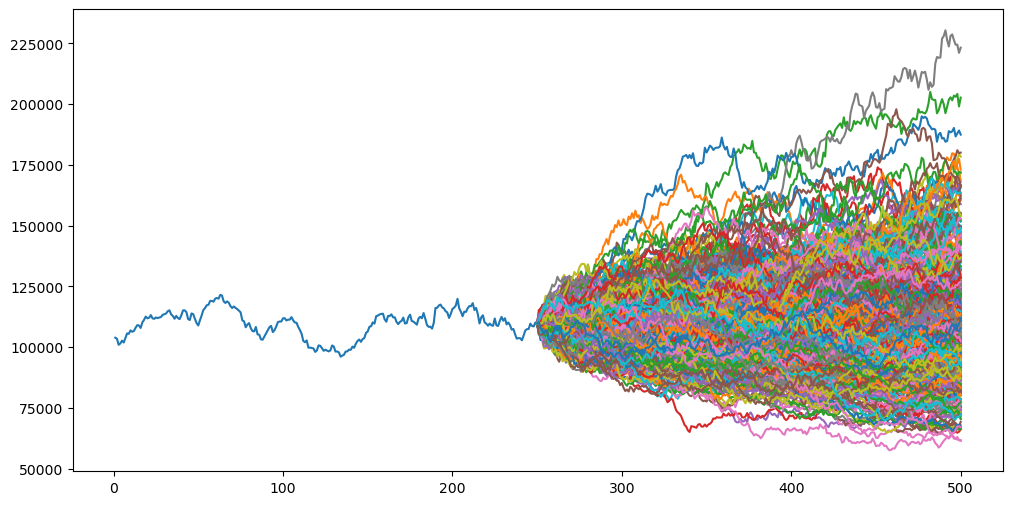
Excelente! Nós geramos 500 curvas utilizando as mesmas propriedades estatísticas do IBOV em 2022. O valor do último fechamento, é, portanto, o valor projetado de cada simulação.
Calculando o VaR da Simulação
As linhas projetadas são legais, mas ainda precisamos tirar a informação mais importante: o VaR, ou Value-at-Risk.
De forma simplificada, pegamos o 5º percentil de todos os fechamentos sintéticos para dizer, com 95% de confiança, que o valor do IBOV em 2023 não deve cair abaixo desse valor.
Você pode calcular o VaR de um ativo ou portfólio na nossa ferramenta de cálculo de VaR.
# Generate VaR line
confidence = 95
var = np.percentile(all_synthetic_closes, 100 - confidence)
print(f"VaR = {round(var, 2)} with confidence = {confidence}%")VaR = 75444.66 with confidence = 95%
Calculando o Break-Even com a SELIC
Uma análise importante que podemos fazer é: em quantos % das vezes a simulação gerou um resultado que foi melhor que a SELIC? Isso é importante para podermos julgar a vantagem (ou não) de se ficar exposto à bolsa.
Para efeitos de projeção, vamos considerar uma SELIC média de 13% para 2023.
# Generate breakeven risk free line
projected_risk_free = 0.13
breakeven_close = last_close * (1 + projected_risk_free)
print(f"Breakeven compared with projected Selic: {round(breakeven_close, 2)}")
above_breakeven = [close for close in all_synthetic_closes if close > breakeven_close]
pct_above_breakeven = len(above_breakeven) / len(all_synthetic_closes)
print(f"Probability above breakeven: {pct_above_breakeven:.2%}")Breakeven compared with projected Selic: 124000.1
Probability above breakeven: 22.00%
Reparem a importância da análise. Não basta que a bolsa fique positiva, mas sim que seja superior à taxa livre de risco. Nesse caso, e para a simulação atual, vemos que o IBOV ficaria acima dos 124k apenas em 22% das vezes.
Plotando todos os gráficos
Vamos recapitular o que fizemos até agora:
- Geramos as zonas de suportes e resistências projetadas, com até 2 desvios-padrão, para 2023;
- Calculamos 500 curvas sintéticas utilizando Monte-Carlo;
- Geramos o VaR dessas curvas com 95% de confiança;
- Calculamos o break-even projetado considerando a taxa livre de risco projetada para 2023.
Para visualizarmos melhor, vamos unir tudo em um mesmo gráfico:
from scipy.stats import norm
from random import random
# Plot closes again
fig = plt.figure(figsize=(12, 6))
plt.plot(days, closes_list)
# Number of simulations, i.e., curves that will be projected
simulations = 500
all_synthetic_closes = []
# Generate synthetic trading days
num_days = [days[-1]]
for i in range(trading_days):
num_days.append(num_days[-1] + 1)
for i in range(simulations):
closes = [last_close]
# Generate synthetic closes
for j in range(trading_days):
pct_change = norm.ppf(random(), loc=mean, scale=std_dev)
synthetic_close = closes[-1] * (1 + pct_change)
closes.append(synthetic_close)
last_synthetic_close = closes[-1]
all_synthetic_closes.append(last_synthetic_close)
plt.plot(num_days, closes)
# Generate supply and demand zones
for factor in factors:
price_zone = round((1 + factor * vol) * last_close, 4)
zones = [price_zone] * trading_days
color = 'darkred' if factor > 0 else 'darkgreen'
plt.plot(
num_days[1:],
zones,
linewidth=3,
linestyle='--',
color=color,
label=f"{factor}σ")
# Generate VaR line
confidence = 95
var = [np.percentile(all_synthetic_closes, 100 - confidence)] * trading_days
plt.plot(
num_days[1:],
var,
linewidth=3,
linestyle='--',
color="black",
label=f"VaR {confidence}%")
# Generate breakeven risk free line
projected_risk_free = 0.13
breakeven_close = last_close * (1 + projected_risk_free)
plt.plot(
num_days[1:],
[breakeven_close] * trading_days,
linewidth=3,
linestyle='--',
color="gold",
label=f"Selic {projected_risk_free:.0%}")
plt.legend(loc='upper left')
plt.show()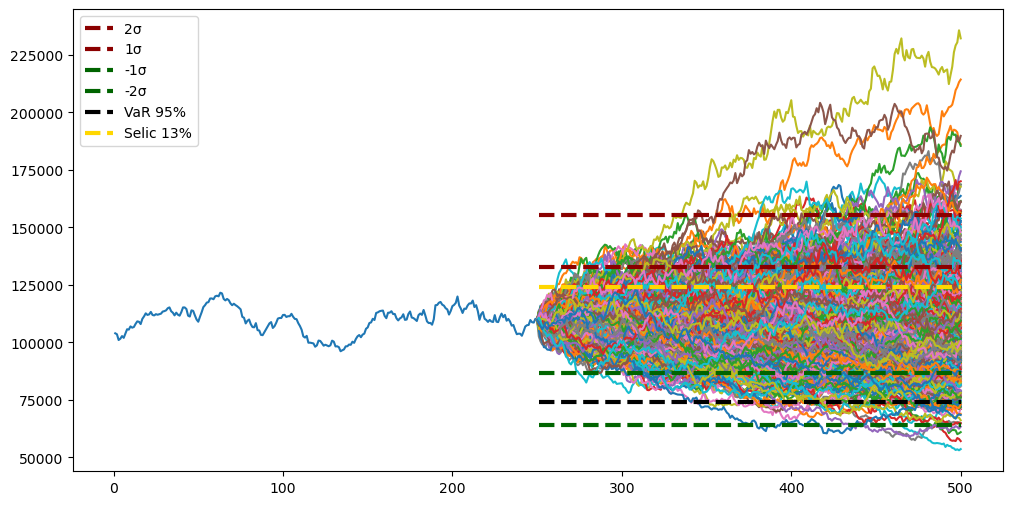
E agora você sabe os pontos de interesse para 2023! Veja de fato como o 2º suporte é bem significativo (pouquíssimas curvas caem abaixo dele), e como a maior parte das simulações ficam, de fato, entre as duas zonas de suporte e resistência principais.
Para finalizar, vamos calcular essas probabilidades:
upper_limit_2 = round((1 + 2 * vol) * last_close, 4)
upper_limit_1 = round((1 + 1 *vol) * last_close, 4)
lower_limit_1 = round((1 - 1 * vol) * last_close, 4)
lower_limit_2 = round((1 - 2 * vol) * last_close, 4)
in_between_1 = [close for close in all_synthetic_closes if close >= lower_limit_1 and close <= upper_limit_1]
in_between_2 = [close for close in all_synthetic_closes if close >= lower_limit_2 and close <= upper_limit_2]
pct_between_1 = len(in_between_1) / len(all_synthetic_closes)
pct_between_2 = len(in_between_2) / len(all_synthetic_closes)
print(f"Probability between -1 and +1 std: {pct_between_1:.2%}")
print(f"Probability between -2 and +2 std: {pct_between_2:.2%}")Probability between -1 and +1 std: 69.40%
Probability between -2 and +2 std: 95.00%
Como esperado, as primeiras zonas de suporte e resistência, por serem baseadas no desvio-padrão, compreendem ~68% das curvas.
Se ampliarmos essas zonas utilizando 2 desvios-padrão, então vemos que exatas 95% das simulações se encaixam nesse range.
Conclusão
Projetar o futuro é sempre complexo, e muitas reputações foram perdidas nesse processo. Nosso objetivo aqui, no entanto, é prover as bases estatísticas que nos deem uma noção do que pode acontecer no próximo ano, de modo que possamos utilizar essas informações para tomar as melhores decisões de investimento.
Por exemplo, vimos que 133k é um ponto de resistência importante, e que qualquer coisa abaixo de 124k é pior que aplicar no Tesouro Direto. Também, 86k é um cenário factível e é importante estar preparado para esse cenário.
No QuantBrasil nós providenciamos diversas ferramentas quantitativas de gestão de risco:
Crie sua conta no QuantBrasil em menos de 1 minuto para aproveitar essas e outras ferramentas quantitativas. Considere assinar o Plano Premium para desbloquear tudo que o QuantBrasil tem a oferecer.
Abraços e um feliz 2023 a todos!