Como Criar uma Simulação de Monte Carlo no Mercado Financeiro Utilizando Python

No artigo de hoje continuaremos nossos estudos focados no gerenciamento de risco, e aprenderemos o conceito por trás da famosa simulação de Monte Carlo.

Começaremos analisando o retorno em um jogo de cassino (que deu origem ao nome), e vamos terminar aplicando os conceitos aprendidos para o mercado financeiro.

Mas o que significa "simulação de Monte Carlo" e de onde surgiu esse método?

A origem da simulação de Monte Carlo

O conceito aplicado à simulação de Monte Carlo foi inventado pelo matemático Stanislaw Ulam (mais conhecido pelo seu trabalho com armas nucleares). De licença do trabalho por estar doente, Ulam começou a jogar Paciência (o jogo de cartas). Como um típico cientista, ele queria calcular a probabilidade de ganhar nesse jogo onde ele só perdia.

Mesmo sendo um grande matemático, Ulam não conseguiu resolver esse problema analíticamente através da combinatória. Restou a ele, portanto, resolver o problema utilizando força bruta: jogar $n$ vezes, contar o número de vitórias, e dividir pelo número de jogos ( $n$ ).

Após diversas partidas, no entanto, ele ainda não tinha conseguido vencer nenhuma vez. Ou seja, esse método poderia levar anos até que se pudesse obter uma boa estimativa. Ele decidiu então usar um computador (ENIAC) com a ajuda de seu amigo, John von Neumann.

Na época, essa simulação demorou algumas horas (enquanto hoje isso seria feito em microsegundos). E com isso foi registrada a primeira simulação de Monte Carlo da história. Interessantemente, eles usaram Monte Carlo para o design da bomba atômica utilizada na segunda guerra, o que mostra que esse método não é aplicável apenas para jogos de cartas.

O que é o método de Monte Carlo?

Definimos o método de Monte Carlo como:

Método usado para estimar valores desconhecidos por meio do princípio da infêrencia estatística.

Você pode estar se perguntando: "mas o que signifca infêrencia estátistica?"

Para entendermos melhor, precisamos definir os conceitos de população e amostra.

Considere população como sendo o universo de todos os exemplos possíveis. No caso do jogo de cartas Paciência, o universo seria todos os possíveis jogos que podem ser jogados. Com certeza, esse número é muito grande!

Agora suponha que dentre todos esses jogos, nós separemos alguns. Essa é a nossa amostra. As estatísticas que obtemos dessa amostra podem ser usadas para fazer uma inferência sobre a população.

Para podermos representar a população por uma amostra, é crucial que a amostragem seja aleatória. Nesse caso, a amostra tende a exibir as mesmas propriedades da população que ela foi retirada (isso é exatamente o que acontece com o random walk).

Mas qual o tamanho ideal da amostra para que possamos ter um alto grau de confiança que ela irá representar estatisticamente a população? Vamos explorar isso com um simples exemplo.

Exemplo 1: a estatística do cara ou coroa

Exemplo1

Suponha que eu lance uma moeda apenas 2 vezes e que ambos os resultados tenham sido cara. O quão confiante você estaria para dizer que o próximo resultado também será cara? Provavelmente não muito, já que não temos dados suficientes para basear a resposta.

Agora considere que eu tenha lançado a moeda 100 vezes e que obtive 100 caras. Você pode começar a imaginar que a moeda tem cara dos dois lados ou está modificada para dar sempre o mesmo resultado. Nesse caso, você teria muito mais confiança que o próximo resultado seria cara.

Por fim, considere que de 100 lançamentos, 52 tenham sido cara e 48 tenham sido coroa. A probabilidade de tirar cara seria de 52/100, certo? Se você tivesse que escolher esse seria o melhor palpite baseado nos dados que temos disponíveis, mas ainda sim não teriamos muita certeza, uma vez que mesmo que você lance uma moeda 100 vezes, dificilmente o resultado será exatos 50x50.

Com esses três exemplos simples de cara ou coroa podemos definir confiança como algo dependente de dois fatores:

O tamanho da amostra (o número de vezes que lançamos a moeda);
A variância da amostra.

No exemplo onde tudo deu cara, os resultados não apresentaram nenhuma variabilidade, enquanto quando quase metade foi cara, a variância dos resultados foi muito alta.

Em suma: quando a variância aumenta, precisamos de um número maior de amostras para manter a confiança no nosso resultado.

Exemplo 2: Roleta em Monte Carlo

Exemplo2

Vamos aprofundar as ideias que aprendemos até aqui aplicando um exemplo prático em Python. Como o nome Monte Carlo foi dado a esse método por ele ser muito usado para jogos de cassino, vamos considerar a famosa roleta.

Para facilitar a nossa vida, resumi-la-emos da seguinte forma:

Apostaremos em um número entre 1 e 36 (simulando os números presentes na roleta, ignorando a cor);
Para cara real apostado ganhamos 36 de volta se a bolinha cair no nosso número (35 dos outros participantes e nosso 1 real de volta);
Se a bolinha cair em outro número, perdemos o dinheiro apostado.

Você já consegue imaginar qual é a probabilidade de vitória nesse jogo?

Para simular esse jogo pelo método de Monte Carlo, vamos começar importando uma biblioteca para nos ajudar a escolher um número aleatório.

import random

O primeiro passo é criar a roleta em si, com números de 1 a 36. Para isso, vamos criar uma lista com esse range de números.

roulette = list(range(1, 37))
print(roulette)

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36]

Vamos então criar uma função para calcular o retorno a cada partida jogada.

Se a bola cair no nosso número, i.e. se o número aleatóriamente gerado for o número previamente escolhido, o retorno liquído será dado pelo valor da nossa aposta vezes o prêmio pela vitória (odds) menos 1.

Por outro lado, se esses números forem diferentes, nós perdemos o valor apostado.

def returns(ball, my_number, bet, odds):
    if ball == my_number:
        return bet * (odds - 1)
    else:
        return -bet

Agora já temos tudo pronto para programarmos o jogo em si. Vamos criar uma função chamada play_roulette que irá receber:

O número de partidas que queremos jogar (number_of_spins);
O número no qual iremos apostar (my_number);
O valor da aposta (bet).

Nossa função vai realizar um for loop no número de partidas e, em cada partida, a bola será escolhida de forma aleátoria entre os valores da nossa roleta.

Vamos criar uma variável chamada my_returns que irá armazenar o retorno acumulado ao final de cada rodada.

Colocando tudo junto, temos:

# Welcome to Monte Carlo! A roulette game adapted from Prof. John Guttag MIT class

def play_roulette(number_of_spins, my_number, bet):
    # Define roulette as a list ranging from 1 to 36
    roulette = list(range(1, 37))

    # The reward is the size of the roulette
    odds = len(roulette)

    my_return = 0

    for i in range(number_of_spins):
        ball = random.choice(roulette)
        my_return += returns(ball, my_number, bet, odds)

    print(f'Average return after {number_of_spins} spins: {my_return / number_of_spins:.2}')

Aplicando a simulação de Monte Carlo

Agora estamos pronto para iniciar a simulação de Monte Carlo!

Vamos supor que iremos ao cassino em 3 dias diferentes (repeat), que em cada dia jogaremos na roleta 100 vezes (number_of_spins), e que sempre apostaremos 1 real (bet) no mesmo número entre 1 e 36 (my_number):

# my_number can be any number between 1 and 36
my_number = 2 
bet = 1

# First game, 100 spins, repeating them 3 times
number_of_spins = 100
repeat = 3
for i in range(repeat):
    play_roulette(number_of_spins, my_number, bet)

Average return after 100 spins: -0.64
Average return after 100 spins: 0.44
Average return after 100 spins: -1.0

Toda vez que rodarmos esse código, obteremos um resultado diferente. No resultado acima, vimos que o retorno médio de cada dia pode variar muito, desde 0.44 até -0.64 por rodada. Se você rodar essa simulação novamente, poderá ter prejuízo todos os dias. Ou seja, existe uma grande variância nos resultados.

Isso se dá pois o tamanho da nossa amostra não é grande o suficiente para inferir estatísticamente o resultado esperado para esse jogo. O que aconteceria se aumentarmos esse número para 1 milhão?

Vamos testar!

# Second game, 1000000 spins, repeating them 3 times
number_of_spins = 1000000
repeat = 3
for i in range(repeat):
    play_roulette(number_of_spins, my_number, bet)

Average return after 1000000 spins: -2.8e-05
Average return after 1000000 spins: 0.0078
Average return after 1000000 spins: -0.004

Interessantemente, para um número maior de jogos o retorno médio é bem próximo a 0 e os resultados são semelhantes para os 3 dias! Ou seja, nesse caso existe menos variância nos resultados.

Mas por que isso acontece?

Lei dos grandes números

Existe um teorema fundamental da teoria da probabilidade chamada de lei dos grandes números.

Basicamente, esse teorema diz que a média dos resultados de uma mesma experiência converge ao Valor Esperado à medida que o número de tentativas tende ao infinito.

Sabemos, da fórmula do EV, que:

$EV = P_{gain} \times payoff + P_{loss} \times risk$

Sendo assim, no exemplo da roleta, temos que:

$EV = \dfrac{1}{36} \times 35 + \dfrac{35}{36} \times -1 = 0$

Uma vez que 1 a cada 36 vezes teremos um lucro de 35 reais, e nas outras 35 vezes teremos um prejuízo de 1 real.

Ou seja, no exemplo acima, a lei dos grandes números diz que se jogarmos na roleta um número infinito de vezes, o retorno esperado será de 0.

Ora, infinito é um número muito grande e como bem sabemos um computador só recebe números finitos. Mas como vimos, um valor de N (o valor da amostra) de 1 milhão já chega muito perto da probabilidade real (e a medida que aumentarmos esse número, mais perto de 0 vamos chegar!).

Conclusão do jogo da roleta

Com esse exemplo simples, em que sabemos facilmente calcular o retorno esperado para um número infinito de jogos, conseguimos com sucesso aplicar e entender melhor o método de Monte Carlo.

Do ponto de vista do cassino, é irrelevante o resultado individual de cada jogador, uma vez que a lei dos grandes números garante que o resultado se aproxima do valor esperado uma vez que o número de jogos se acumula.

Quer dizer então que o retorno do cassino tende a 0%?

Claro que não! Como bem sabemos, the house always wins! Por isso que dificilmente você vai encontrar um jogo de roletas com 36 números em um cassino. O mais comum é a roleta europeia, que além dos 36 números possui o número 0, ou a roleta americana, que além dos 36 números e do 0 ainda possui o 00. E como você provavelmente já entendeu, se a bolinha cair no número 0 ou 00, o cassino ganha e todo mundo perde.

Como exercício, tente modificar o código acima para calcular o retorno da roleta européia e americana!

Simulação de Monte Carlo aplicada ao mercado financeiro

Agora que já entendemos como funciona a simulação de Monte Carlo e sabemos como programá-la, vamos ao que interessa: descobrir como podemos utilizá-la no mercado financeiro.

Nosso objetivo é muito simples: gerar um determinado número de simulações (que já sabemos que deve ser relativamente grande) para criar retornos diários sintéticos (artificiais) para um determinado portfólio.

Com esses resultados, podemos continuar nossas análises de gerenciamento de risco e calcular o VaR desse portfólio.

Vamos analisar esse problema passo-a-passo!

Importando as bibliotecas necessárias

Começaremos carregando as bibliotecas que vamos usar. Para quem já vem acompanhando os nossos artigos, a única novidade aqui é a biblioteca de álgebra linear do numpy.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from numpy import linalg as LA

Criando o portfólio

Para montar o nosso portfólio, vamos supor que temos uma carteira com os 10 primeiros ativos ranqueados por momentum.

O arquivo .csv estará disponível no nosso grupo do Telegram.

df = pd.read_csv('../data/D1/MonteCarlo-portfolio.csv', index_col='datetime', parse_dates=True)
df = df.pivot_table(index='datetime',columns='symbol',values='close')
df.head()

symbol	CPFE3	ELET3	ELET6	HYPE3	LOGN3	RECV3	RRRP3	SLCE3	SMTO3	UNIP6
datetime
2021-06-01	24.85	44.01	42.87	35.68	19.87	16.18	41.19	44.58	33.05	76.98
2021-06-02	24.84	44.17	43.02	35.11	20.20	16.17	41.40	44.81	33.46	83.64
2021-06-04	25.12	44.77	44.02	34.74	19.92	16.68	41.24	44.45	33.68	84.46
2021-06-07	25.22	45.53	44.41	35.83	19.86	16.31	40.07	43.88	33.52	75.81
2021-06-08	25.02	44.40	43.04	34.70	19.45	16.05	40.01	43.72	33.63	71.48

Com a nossa carteira pronta, vamos salvar em uma variável o número de ativos que temos na nossa carteira (que será necessário na próxima parte) e calcular o retorno diário da carteira.

# calculating number of assets in our portfolio
number_of_assets = len(df.columns)
print(f'We have {number_of_assets} assets in our portfolio.')

# calculating daily returns
returns = df.pct_change().dropna()

returns.head()

We have 10 assets in our portfolio.

symbol	CPFE3	ELET3	ELET6	HYPE3	LOGN3	RECV3	RRRP3	SLCE3	SMTO3	UNIP6
datetime
2021-06-02	-0.000402	0.003636	0.003499	-0.015975	0.016608	-0.000618	0.005098	0.005159	0.012405	0.086516
2021-06-04	0.011272	0.013584	0.023245	-0.010538	-0.013861	0.031540	-0.003865	-0.008034	0.006575	0.009804
2021-06-07	0.003981	0.016976	0.008860	0.031376	-0.003012	-0.022182	-0.028371	-0.012823	-0.004751	-0.102415
2021-06-08	-0.007930	-0.024819	-0.030849	-0.031538	-0.020645	-0.015941	-0.001497	-0.003646	0.003282	-0.057116
2021-06-09	-0.021982	-0.000225	0.001162	-0.014409	-0.001542	0.000623	-0.011497	-0.002059	0.062147	0.013151

Vamos supor por simplicidade que os pesos dos ativos na carteira são iguais. Note que você pode modificar de acordo com a sua carteira e que esses valores podem ser calculados utilizando o ATR .

weights = [0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1]

print(f'portfolio weights: {weights},\nsum of weights: {sum(weights):.2f}')

portfolio weights: [0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1],
sum of weights: 1.00

Criando séries temporais sintéticas

Agora chegamos num ponto chave para a nossa simulação. A idéia aqui é criar séries temporais (no nosso caso, séries de retornos) sintéticas (artificiais) com propriedades estatísticas similares às da série original.

Ou seja, vamos criar N diferentes séries temporais de retornos diários que possuam média, variância e covariância similares às do nosso retorno calculado anteriormente.

Mas como isso é possível? Graças a uma distribuição normal multidimensional. Basicamente ela é uma generalização da distribuição normal que conhecemos para dimensões maiores que 1. Com ela é possível transformar um vetor aleatório qualquer em um novo vetor que obedece uma distribuição normal e possui propriedades estatísticas similares às dos dados que queremos transformar.

Matemáticamente, os retornos sintéticos podem então ser descritos da seguinte maneira:

$\text{Returns}_{\text{synthetic}} = \mu_{\text{original}} + R_{\text{pdf}} \times L.$

Parece complicado? Calma que vou explicar cada termo individualmente:

$\mu_{\text{original}}$ é a média dos dados originais. No nosso caso, cada retorno dos ativos da nossa carteira vai possuir uma média, no intervalo de tempo que carregamos os nossos dados.
$R_{pdf}$ é uma matriz onde cada coluna corresponde a um vetor aleatóriamente gerado, com base em algum tipo de pdf (do inglês probability density function). Existem funções próprias do Python (e em outras linguagens também) que nos possibilita criar distribuições normais com valores aleatórios.
$L$ é uma matriz triangular inferior proveniente de uma decomposição de Cholesky da matriz de covariância dos dados originais. Nossa, agora complicou né?! Calma que eu explico. Como diria Jack, o estripador, vamos por partes.

Uma matriz de covariância é uma matriz simétrica que relaciona a covariância entre as variáveis. No nosso caso, é uma matriz que mostra a covariância entre os ativos da carteira. Lembre-se que covariância é definida como uma medida de como duas variáveis variam conjuntamente. A correlação pode ser vista como uma normalização da covariância.

Uma decomposição de Cholesky é um tipo de fatoração usada para decompor uma matriz em um produto de uma matriz triangular inferior vezes a sua transposta (que será triangular superior).

Uma matriz triangular é uma matriz onde os elementos acima ou abaixo da diagonal são nulos. Como você pode imaginar, uma matriz é chamada de triangular inferior quando os elementos acima da diagonal são zero (e diagonal superior quando os elementos abaixo da diagonal são zero).

Agora que entendemos todos os termos da nossa equação, podemos calculá-la seguindo esses 4 passos:

Calcular a matriz de covariância dos nossos dados originais;
Criar uma matriz aleatória seguindo algum tipo de pdf;
Fazer uma decomposição de Cholesky da matriz de covariância original;
Multiplicar a decomposição pela matriz de valores aleatório e somar a média dos retornos originais.

Pronto! Ao final desses 4 passos, vamos ter gerado com sucesso uma matriz com retornos sintéticos aleatórios, com estatísticas similares as dos dados originais!

Primeiro passo: calcular a matriz de covariância

Vamos comecar calculando a matriz de covariância dos retornos originais. Para isso, podemos usar a função cov.

cov_returns = returns.cov()
cov_returns

symbol	CPFE3	ELET3	ELET6	HYPE3	LOGN3	RECV3	RRRP3	SLCE3	SMTO3	UNIP6
symbol
CPFE3	0.000267	0.000174	0.000168	0.000101	0.000035	0.000127	0.000076	0.000045	0.000091	0.000050
ELET3	0.000174	0.000567	0.000504	0.000179	0.000146	0.000262	0.000224	0.000080	0.000174	0.000146
ELET6	0.000168	0.000504	0.000485	0.000155	0.000139	0.000244	0.000206	0.000067	0.000149	0.000154
HYPE3	0.000101	0.000179	0.000155	0.000335	0.000115	0.000175	0.000175	0.000029	0.000104	0.000077
LOGN3	0.000035	0.000146	0.000139	0.000115	0.000924	0.000207	0.000153	0.000092	0.000106	0.000070
RECV3	0.000127	0.000262	0.000244	0.000175	0.000207	0.001153	0.000650	0.000228	0.000261	0.000286
RRRP3	0.000076	0.000224	0.000206	0.000175	0.000153	0.000650	0.001052	0.000263	0.000221	0.000266
SLCE3	0.000045	0.000080	0.000067	0.000029	0.000092	0.000228	0.000263	0.000622	0.000227	0.000093
SMTO3	0.000091	0.000174	0.000149	0.000104	0.000106	0.000261	0.000221	0.000227	0.000467	0.000140
UNIP6	0.000050	0.000146	0.000154	0.000077	0.000070	0.000286	0.000266	0.000093	0.000140	0.000647

Segundo passo: criar uma matriz aleatória

Agora podemos criar a matriz de valores aleatórios. Para esse artigo, iremos escolher valores aleatórios distribuidos de acordo com uma distribuição normal. Para isso, utilizaremos a função random.normal da biblioteca numpy.

Perceba que devemos gerar um vetor de valores aleatórios para cada ativo da nossa carteira, e colocá-los lado a lado para formar uma matriz. Mas qual será o tamanho desse vetor, ou melhor, quantos retornos sintéticos precisamos criar?

Essa pergunta é muito importante e a escolha desse número será discutida com mais detalhes em breve. Vamos assumir por enquanto que queremos gerar dados artificiais para os próximos 300 dias.

Matemáticamente isso significa que queremos criar, para o nosso exemplo, uma matriz com 300 linhas e 10 colunas (uma para cada ativo). Em Python, podemos especificar esse tamanho com a tupla size contendo o número de linhas e colunas que queremos criar, respectivamente.

number_of_synthetic_returns = 300

random_matrix = np.random.normal(size=(number_of_synthetic_returns, number_of_assets))

print(f'The random generated matrix has {len(random_matrix)} rows and {len(random_matrix.T)} columns.')

The random generated matrix has 300 rows and 10 columns.

Terceiro passo: decomposição de Cholesky

Com a nossa matriz aleatória pronta, podemos partir para a decomposição da matriz de covariância. Aqui, diferentes decomposições podem ser usadas, autovalor, valor singular ou Cholesky.

Vamos usar uma decomposição de Cholesky por ser mais simples e computacionalmente menos custosa em relação às outras. Calcular essa decomposição em Python é muito simples, precisamos apenas chamar a função cholesky da biblioteca de álgebra linear que carregamos lá no começo.

# Cholesky decomposition of a Hermitian, positive-definite matrix A in the form A = L L*
L = LA.cholesky(cov_returns)

Lembra que falamos que essa decomposição vai gerar uma matriz triangular inferior? Para verificar isso, podemos usar a função spy da biblioteca matplotlib. Essa função retorna um pixel preto para valores não-nulos e branco para valores nulo.

plt.figure(figsize=(1,1))
plt.spy(L)
plt.show()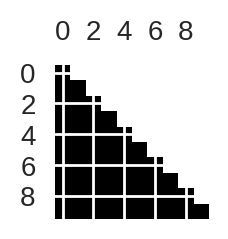

Quarto passo: aplicar operações algébricas

O último passo é multiplicar a matriz L originada da decomposição de Cholesky da matriz de valores aleatórios e somar a média dos dados originais.

A multiplicação não tem mistério nenhum, mas para que possamos realizar essa soma, temos que ter matrizes com as mesmas dimensões. Repare que a dimensão final dos retornos sintéticos nesse exemplo é 300 $\times$ 10 (number_of_synthetic_returns $\times$ number_of_assets).

O nosso vetor com as médias possui apenas os valores da média de cada ativo na nossa carteira (que no nosso caso específico são 10). A idéia então é repetir esses valores em todas as linhas, até chegar ao mesmo número de linhas da matriz de retornos sintéticos.

Ou seja, temos um vetor com as médias:

$x = \begin{pmatrix} \rm media_1, media_2, ..., media_n \end{pmatrix}$

E queremos criar uma matriz:

$X = \begin{pmatrix} \rm media_1 &\rm media_2 & \rm ... &\rm media_n \\ \rm media_1 &\rm media_2 & \rm ... & \rm media_n \\ \vdots & \vdots & \vdots & \vdots \\ \rm media_1 & \rm media_2 & \rm ... & \rm media_n \end{pmatrix}_{\rm N \times n}$

Onde N é o número de retornos sintéticos e n é o numero de ativos no nosso portfólio.

Existem diferentes maneira de se realizar esse processo; uma maneira simples é multiplicar o vetor com as médias por uma matriz unitária (np.ones), com as dimensões exatas que queremos. Dessa forma, nosso output será exatamente a matriz que mostramos no exemplo acima.

Como o vetor de médias não tem o número de linhas iguais à da matriz unitária, passamos o valor None como o número de linhas e : para usarmos todas as colunas.

shape = [number_of_synthetic_returns, number_of_assets]
mean_returns = returns.mean()[None,:] * np.ones(shape=shape)

Por fim, agora que todo mundo está com as dimensões corretas, podemos aplicar o produto interno e somar a média para criar a nossa matriz de retornos sintéticos!

Vamos colocar ela em um DataFrame para ajudar na visualização dos resultados.

synthetic_returns = mean_returns + np.inner(random_matrix,L)
synthetic_returns = pd.DataFrame(synthetic_returns, columns=df.columns)
synthetic_returns

symbol	CPFE3	ELET3	ELET6	HYPE3	LOGN3	RECV3	RRRP3	SLCE3	SMTO3	UNIP6
0	-0.002673	0.002827	0.014804	-0.001614	0.019460	0.052907	-0.012176	-0.041724	-0.029560	0.023030
1	0.007756	0.004208	0.009196	-0.024263	0.050465	0.017520	0.001956	0.019458	-0.019743	0.010354
2	-0.002652	-0.006182	-0.008852	-0.008537	-0.059138	-0.011053	0.001519	0.001241	0.014663	0.030116
3	-0.002179	-0.035758	-0.025067	0.009455	-0.084413	-0.008850	-0.002463	-0.015798	-0.007175	-0.015308
4	0.013328	0.000411	-0.001383	0.009724	-0.088576	-0.091792	-0.014631	-0.033452	-0.016267	-0.015138
...	...	...	...	...	...	...	...	...	...	...
295	-0.008006	0.036114	0.022945	0.020048	0.014422	-0.003381	-0.010643	-0.004911	0.037388	0.027960
296	-0.001122	0.014123	0.012441	0.036578	-0.025932	0.016442	-0.008930	0.006759	0.005430	0.006759
297	-0.017059	-0.028187	-0.031189	-0.005637	0.028680	-0.009012	-0.016838	-0.015652	0.007645	-0.023138
298	-0.011925	-0.068186	-0.062905	0.001613	-0.003474	-0.035214	-0.097712	-0.047208	-0.045475	0.010562
299	-0.007982	0.002892	0.012652	0.001107	0.025533	-0.048929	-0.047662	0.011084	0.010250	-0.018370

300 rows × 10 columns

Pronto! Acabamos de criar séries temporais sintéticas (artificiais) de retornos para todos os ativos da nossa carteira!

A Simulação de Monte Carlo

Com todos os passos anteriores entendidos, estamos prontos para comecar a simulação de Monte Carlo!

A única coisa que precisamos fazer é repetir o procedimento de criar esses retornos sintéticos um número N de vezes para que possamos simular diferentes resultados para o portfólio ao longo do tempo.

Para facilitar a nossa vida, vamos colocar todos os passos anteriores numa função chamada monte_carlo_sim e criar um for loop para repetir os cálculos N vezes.

Para a nossa função, além dos parâmetros que já foram explicados anteriormente, vamos também adicionar um valor de um capital inicial, de modo a podermos calcular o retorno do portfólio em cima do capital para cada simulação.

Utilizaremos a função cumprod da biblioteca numpy para calcular o produto cumulativo dos retornos em cima do capital (lembre-se que os retornos funcionam igual a juros compostos!)

Ao final, a função irá retornar a curva de capital para cada simulação e também o valor dos retornos sintéticos da última iteração, apenas para podermos verificar as propriedades estatísticas dos resultados (poderia ser de qualquer iteração).

# Monte Carlo simulation

def monte_carlo_sim(n_iterations, number_of_synthetic_returns, data, weights, initial_capital):

    mean_returns = data.mean()[None,:] * np.ones([number_of_synthetic_returns, len(data.columns)])

    portfolio_returns = np.zeros([number_of_synthetic_returns, n_iterations]) 

    L = LA.cholesky(data.cov()) # Cholesky decomposition

    size = (number_of_synthetic_returns, len(weights))
    
    for i in range(n_iterations):
        random_matrix = np.random.normal(size=size)

        synthetic_returns = mean_returns + np.inner(random_matrix, L)

        portfolio_returns[:,i] = np.cumprod(np.inner(weights, synthetic_returns) + 1) * initial_capital 
    
    # returns the capital curve from all simulations 
    # and the synthetic returns of the last simulation, for verification purposes only
    return portfolio_returns, synthetic_returns

Agora podemos rodar o código selecionando os parâmetros necessários.

number_of_synthetic_returns = 300
n_iterations = 1000
initial_capital = 10000

portfolio_returns, synthetic_returns = monte_carlo_sim(
  n_iterations,
  number_of_synthetic_returns,
  returns,
  weights,
  initial_capital
)

E plotar os resultados!

plt.plot(portfolio_returns, linewidth=1)
plt.ylabel('Capital')
plt.xlabel('Days')
plt.show()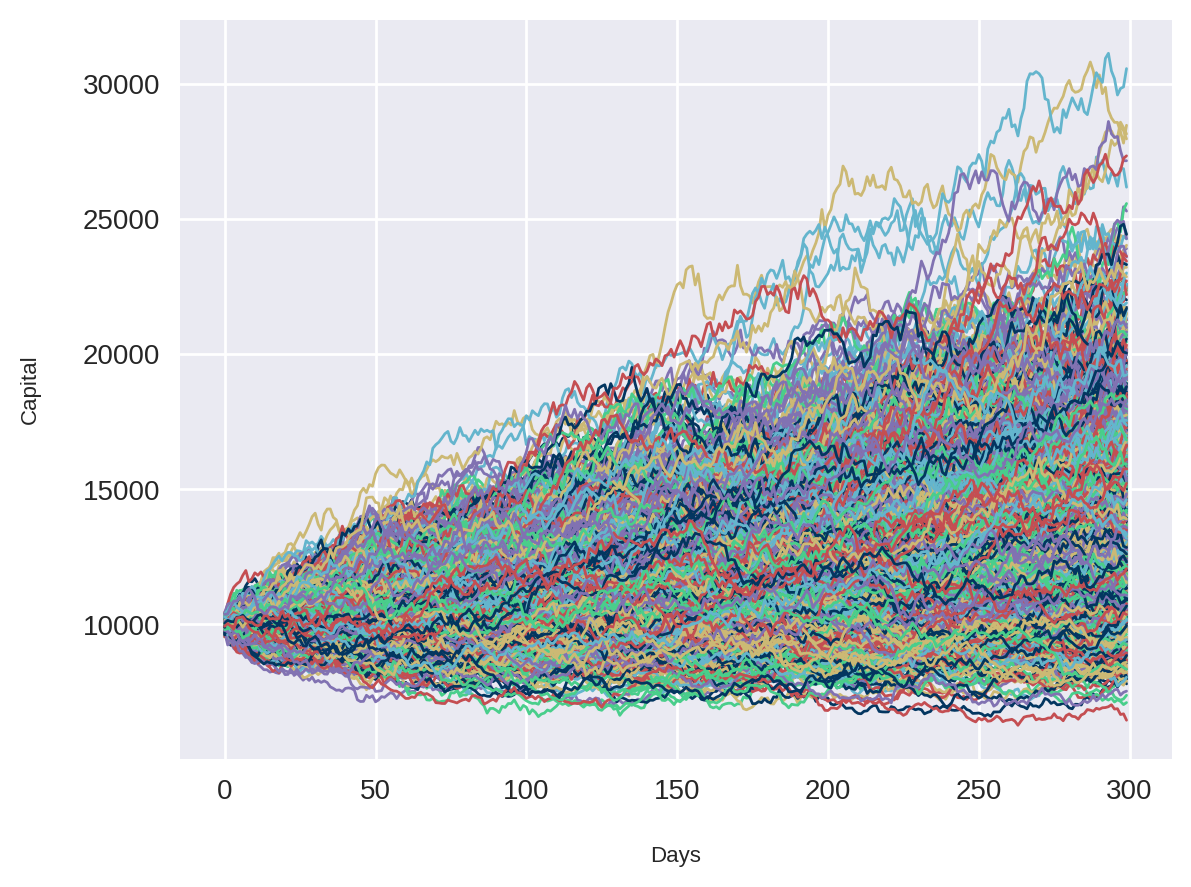

Cada curva do gráfico acima foi gerado com base em uma simulação de Monte Carlo, com os retornos sintéticamente gerados. De cara já conseguimos observar que esse portfólio parece ter um maior número de ganhos do que perdas, visto que a maioria das curvas estão acima do capital inicial de R$10000.

Verificando os resultados

Lembra que eu mencionei que os retornos sintéticos que criamos possui algumas propriedades estatísticas similares ao retorno original?

Pois então, vamos comparar a covariância entre os dados originais e os dados sintéticos. Para os dados originais já temos a matriz de covariância calculada:

cov_returns

symbol	CPFE3	ELET3	ELET6	HYPE3	LOGN3	RECV3	RRRP3	SLCE3	SMTO3	UNIP6
symbol
CPFE3	0.000267	0.000174	0.000168	0.000101	0.000035	0.000127	0.000076	0.000045	0.000091	0.000050
ELET3	0.000174	0.000567	0.000504	0.000179	0.000146	0.000262	0.000224	0.000080	0.000174	0.000146
ELET6	0.000168	0.000504	0.000485	0.000155	0.000139	0.000244	0.000206	0.000067	0.000149	0.000154
HYPE3	0.000101	0.000179	0.000155	0.000335	0.000115	0.000175	0.000175	0.000029	0.000104	0.000077
LOGN3	0.000035	0.000146	0.000139	0.000115	0.000924	0.000207	0.000153	0.000092	0.000106	0.000070
RECV3	0.000127	0.000262	0.000244	0.000175	0.000207	0.001153	0.000650	0.000228	0.000261	0.000286
RRRP3	0.000076	0.000224	0.000206	0.000175	0.000153	0.000650	0.001052	0.000263	0.000221	0.000266
SLCE3	0.000045	0.000080	0.000067	0.000029	0.000092	0.000228	0.000263	0.000622	0.000227	0.000093
SMTO3	0.000091	0.000174	0.000149	0.000104	0.000106	0.000261	0.000221	0.000227	0.000467	0.000140
UNIP6	0.000050	0.000146	0.000154	0.000077	0.000070	0.000286	0.000266	0.000093	0.000140	0.000647

Vamos pegar os dados sintéticos da última simulação que temos e calcular a covariância entre os resultados.

pd.DataFrame(synthetic_returns,columns=df.columns).cov()

symbol	CPFE3	ELET3	ELET6	HYPE3	LOGN3	RECV3	RRRP3	SLCE3	SMTO3	UNIP6
symbol
CPFE3	0.000249	0.000162	0.000155	0.000097	0.000060	0.000170	0.000111	0.000044	0.000068	0.000031
ELET3	0.000162	0.000559	0.000496	0.000189	0.000194	0.000335	0.000235	0.000066	0.000160	0.000128
ELET6	0.000155	0.000496	0.000477	0.000177	0.000198	0.000324	0.000231	0.000061	0.000120	0.000113
HYPE3	0.000097	0.000189	0.000177	0.000331	0.000137	0.000249	0.000237	0.000044	0.000096	0.000044
LOGN3	0.000060	0.000194	0.000198	0.000137	0.001070	0.000343	0.000211	0.000107	0.000139	0.000006
RECV3	0.000170	0.000335	0.000324	0.000249	0.000343	0.001283	0.000700	0.000337	0.000294	0.000235
RRRP3	0.000111	0.000235	0.000231	0.000237	0.000211	0.000700	0.001024	0.000311	0.000239	0.000242
SLCE3	0.000044	0.000066	0.000061	0.000044	0.000107	0.000337	0.000311	0.000654	0.000230	0.000062
SMTO3	0.000068	0.000160	0.000120	0.000096	0.000139	0.000294	0.000239	0.000230	0.000476	0.000075
UNIP6	0.000031	0.000128	0.000113	0.000044	0.000006	0.000235	0.000242	0.000062	0.000075	0.000671

Note que os valores estão perto, mas ainda existe uma diferença. A proximidade é uma função do número de amostras que simulamos, ou seja, o número de retornos sintéticos gerados. Quanto maior esse número, mais próximo da matriz de covariância vamos estar (teste você mesmo!).

Calculando o VaR de um portfólio usando Monte Carlo

Para finalizarmos esse artigo com chave de ouro, vamos usar a função de Monte Carlo que criamos acima para calcular o VaR do portfólio.

Esse procedimento fica muito simples já que conseguimos facilmente extrair o valor do capital total ao final de cada simulação.

last_returns = portfolio_returns[number_of_synthetic_returns - 1, :]
last_returns[:5]

array([15561.28704709, 22561.21386174, 11553.83419122, 15338.13548691,
       20179.40386405])

Agora, em apenas uma linha de código, podemos calcular o VaR com (100 - alpha)% de confiança, utilizando a função percentile da biblioteca numpy.

Para essa função, precisamos apenas dos últimos retornos acumulados e da confiança.

# We are using: 1 - alpha = 99% confidence level
alpha = 1 
VaR = np.percentile(pd.Series(last_returns), alpha)

print(f'We have {100-alpha}% confidence that our selected portfolio of R${initial_capital:.0f} will not decrease to less than R${VaR:.2f} in {number_of_synthetic_returns} days.')
print(f'In {alpha}% of our simulations, the total portfolio losses were greater than R${initial_capital - VaR:.2f} in {number_of_synthetic_returns} days.')

We have 99% confidence that our selected portfolio of R$10000 will not decrease to less than R$8062.05 in 300 days.
In 1% of our simulations, the total portfolio losses were greater than R$1937.95 in 300 days.

Para uma melhor visualização dos resultados, podemos plotar novamente a curva de capital de todas as simulações junto com os valores do capital inicial e do VaR.

plt.plot(portfolio_returns, linewidth=1)
plt.ylabel('Capital Evolution')
plt.xlabel('Days')
plt.axhline(y=initial_capital, color='k', label='Initial')
plt.axhline(y=VaR, color='k', linestyle='--', label='VaR 1%')
plt.legend(loc='upper left')
plt.show()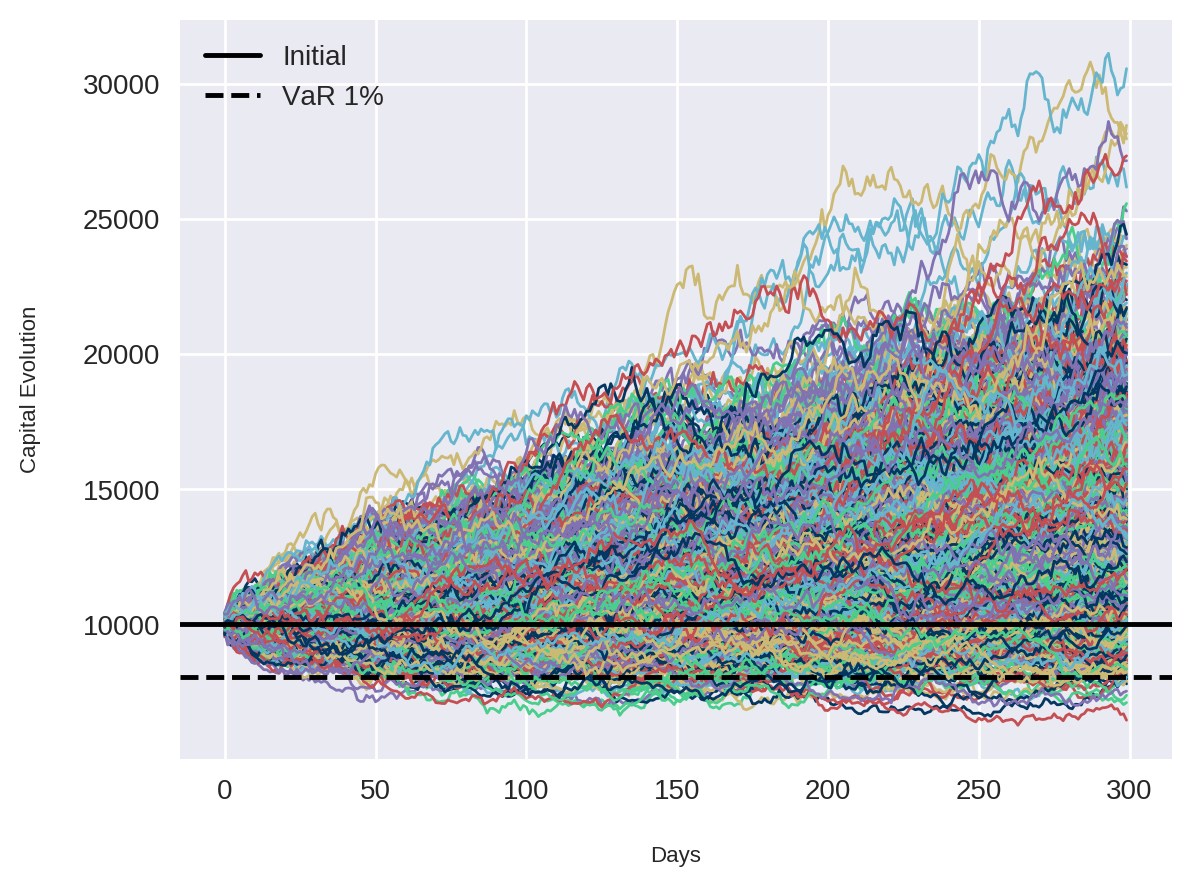

Conclusões finais

No artigo de hoje conseguimos entender melhor o que significa uma simulação de Monte Carlo, da onde ela surgiu, e também o porquê dela funcionar.

Começando com exemplos simples de cara ou coroa e de um jogo de roleta de um cassino, entendemos os conceitos básicos por trás desse método e como programá-lo em Python.

Mudando nossa atenção para o mercado financeiro, aplicamos os conceitos que aprendemos para calcular retornos diários sintéticos (artificiais) que possuem algumas propriedades estatísticas (como média e covariância) similares às dos nossos retornos originais.

Com isso, simulamos o comportamento de um portfólio ao longo de um determinado período, dado um valor de capital inicial.

Por fim, usamos os resultados dessa simulação para calcular o VaR desse portfólio, sem precisar recorrer a abordagens paramétricas (como o caso do cálculo do VaR por dados históricos ou pelo método da variância / covariância).

Reforçando que os dados que foram utilizados aqui estarão disponíveis no nosso grupo do Telegram.

Não se esqueça de criar uma conta no nosso site para ficar por dentro de tudo que rola aqui no QuantBrasil! Sendo membro Premium você desbloqueia todas as estratégias, ativos e timeframes no nosso simulador, além de outras ferramentas imprescindíveis para investidores e traders. Confira nossos planos!

Um abraço e até a próxima!