Como Treinar e Testar o Modelo Long & Short por Cointegração na Prática

Em 25/11/2021

No artigo de hoje vamos dar continuidade ao nosso estudo sobre Long & Short (L&S) por cointegração.

Recapitulando, aprendemos no primeiro artigo dessa série o conceito de séries estacionárias e não-estacionárias, e vimos que devemos procurar por estacionaridade no resíduo entre um par de ativos que estamos interessados. Vimos também que esse resíduo é calculado por meio de uma regressão linear e que o teste de Dickey-Fuller é o mais usado para descobrir se o resíudo é realmente estacionário em um determinado intervalo de tempo.

Já no segundo artigo da série, estudamos a importância na escolha da janela de tempo que utilizamos quando calculamos o modelo linear. Vimos que, embora existam diversas abordagens, um período de 250 dias é uma escolha comum.

Nesse terceiro artigo da série vamos aprender como efetivamente aplicar essa estratégia na prática.

Para isso, vamos ter que separar os nosso dados em duas fases:

A primeira parte, chamada de fase de treino, será utilizada para calcular se o resíduo é estacionário e se o par está cointegrado para diferentes janelas de tempo. Aqui, vamos obter o modelo linear que vamos utilizar na fase seguinte.
A segunda fase será utilizada para testar se o modelo linear encontrado possui retornos à média a partir de um específico ponto de entrada. Em outras palavras, é o backtest da cointegração.

Com isso, vamos aprender a identificar esses sinais de entrada, assim como definir o nosso alvo e stop.

Ansioso?! Então mãos-à-obra e vamos nessa!

Importando as bibliotecas

Vamos começar importando as bibliotecas que vamos usar no nosso estudo.

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from statsmodels.tsa.stattools import adfuller

Definindo nossos ativos

O primeiro passo para começar a análise é definir os dois ativos que queremos estudar. Nos artigos anteriores vinhamos analisando o par PETR3 e PETR4. Contudo, como esse par é muito batido, fica difícil aplicar a estratégia pois ele é constantemente arbitrado.

Portanto, para o estudo de hoje, vamos escolher um ativo de varejo, Lojas Renner (LREN3), e uma construtora, JHSF (JHSF3) como nosso par para análise. Provavelmente esse não é o típico par que você esperaria ver, certo?! Porém, essa é uma das grandes belezas da cointegração: encontrar verdades matemáticas "escondidas" no mercado financeiro.

Será que esse par vai estar cointegrado?

Os arquivos csv utilizados aqui estarão disponíveis no nosso grupo do Telegram. Note que estamos utilizando a opção parse_dates para converter o nosso index do tipo string para o tipo datetime.

Para juntar os dados no mesmo dataframe, usamos a função pd.merge do Pandas e escolhemos a coluna datetime como elemento comum entre eles.

Lembre-se que a ordem dos ativos importa no estudo de cointegração. Na nossa análise, JHSF3 será o ativo base (Base Asset) e LREN3 o ativo de comparação (Comparison Asset). Curioso para saber como seriam os resultados trocando a ordem? Tente rodar no seu computador como dever de casa!

JHSF_DATA = pd.read_csv(
  '../data/D1/JHSF3-D1-cointegracao.csv', 
  index_col='datetime', 
  parse_dates=['datetime']
)["close"]

LREN_DATA = pd.read_csv(
  '../data/D1/LREN3-D1-cointegracao.csv', 
  index_col='datetime', 
  parse_dates=['datetime']
)["close"]

stocks = pd.merge(JHSF_DATA, LREN_DATA, on='datetime')

stocks.columns = ['Base Asset','Comparison Asset']

stocks

	Base Asset	Comparison Asset
datetime
2020-05-08	3.44	30.45
2020-05-11	3.29	29.38
2020-05-12	3.23	29.72
2020-05-13	3.20	28.55
2020-05-14	3.40	29.92
...	...	...
2021-11-10	5.57	32.76
2021-11-11	5.65	33.93
2021-11-12	5.48	32.23
2021-11-16	5.18	31.21
2021-11-17	5.05	30.86

380 rows × 2 columns

Separando os nossos dados

Para dar sequência ao nosso estudo vamos separar os nosso dados em duas partes: treino e teste.

A parte de treino será usada para calcular a estacionariedade do resíduo para diversos intervalos de tempo. Se a maioria deles for estacionário, vamos aceitar a cointegração do par e escolher um intervalo para calcular o modelo linear (normalmente 250 dias).

Com isso, podemos prosseguir para a fase de teste, onde vamos utlizar esse modelo para procurar por possíveis trades.

Nessa análise, vamos separar os dados de treino por um período de 250 dias e testar para os próximos 130 dias.

Ao final dos 130 dias, podemos reavaliamos os últimos 250 dias pra verificar se a cointegração ainda existe. Se sim, nós mantemos a estratégia. Se não, paramos e vamos em busca de um novo par.

Exemplificando:

Dia 1 ao 250: avaliar se o par está cointegrado.
- Caso esteja cointegrado, aplicar a estratégia do dia 251 ao dia 380.
No dia 381, testar a cointegração no período 131 a 380.
- Caso esteja cointegrado, continuar aplicando a estratégia do dia 381 ao 510.
Assim em diante...

Parece complicado? Calma que vamos entender melhor com o exemplo a seguir.

O primeiro passo é separar os nossos dados em treino e teste pelo período de tempo que determinamos.

time_train = 250
stocks_train = stocks.iloc[:time_train].copy()
print(f"Tamanho da base de treino: {len(stocks_train)}")

time_test = 130
stocks_test = stocks.iloc[time_train:time_train + time_test].copy()
print(f"Tamanho da base de teste: {len(stocks_test)}")

Tamanho da base de treino: 250
Tamanho da base de teste: 130

Fase de treino

Essa primeira fase pode ser dividida em 3 passos, que são os passos que aprendemos nos artigos anteriores. Eles são:

Definir quantas janelas de tempo devem possuir o resíduo estacionário para aceitarmos a cointegração.
Treinar um modelo linear com os dados do par escolhido para análise.
Verificar se o resíduo é estacionário com pelo menos 95% de confiabilidade para os intervalos escolhidos.

Para isso, vamos combinar as funções que programamos nos últimos dois artigos. Aqui, apenas uma pequena mudança é feita: retornaremos também o valor do coeficiente angular, $\beta$ , quando calculamos o resíduo pela regressão linear.

def calculate_residual(df, time_period):
    
    df = df.iloc[-time_period:].copy()
    # values converted into a numpy array
    # '-1' to calculate the dimension of rows, and '1' to have only 1 column
    X_independent = df.iloc[:,1].values.reshape(-1, 1)  
    Y_dependent   = df.iloc[:,0].values.reshape(-1, 1) 

    # performing the linear regression
    reg = LinearRegression().fit(X_independent, Y_dependent)   

    # get the angular coef.
    beta = reg.coef_[0][0]
    
    # get the predicted Y given X from the model
    Y_predict  = reg.predict(X_independent)  
    
    # attaching the residual (Y_dependent-Y_predict) from a numpy array to a pandas series
    df['Residual'] = Y_dependent - Y_predict
  
    return df, beta

def check_stationary(df, time_periods, min_confidence=95):
  # initialising an empty list that will receive the output
  stationary_intervals = []

  # loop over the list for all time periods
  for t in time_periods:  
    
    # call the function to calculate the residuals
    residual, beta = calculate_residual(df, t)

    # performing the Augmented Dickey-Fuller test in the residual
    residual_test = adfuller(residual['Residual'])
    
    # calculating the condidence in percentage from the p-value (index 1 of the output test)
    confidence = 100 * (1 - residual_test[1])
   
    # testing for stationarity given a threshold   
    if confidence >= min_confidence:  
      stationary_intervals.append(True)
    else:  
      stationary_intervals.append(False)
  
  # return the interval and if it is stationary
  return stationary_intervals

Com isso podemos facilmente calcular se o resíduo do par escolhido na fase de treino é estacionário.

Para fortalecer ainda mais a nossa análise, vamos definir 8 intervalos de tempo em no máximo 250 dias e aceitar a cointegração apenas se o resíduo for estacionário para pelo menos 5 desses intervalos (mais da metade).

Lembre-se que a variável time_periods é uma lista de intervalos.

time_periods = [120, 140, 160, 180, 200, 220, 240, 250]
min_confidence = 95

is_stationary = check_stationary(stocks_train, time_periods, min_confidence)

for time, stationary in zip(time_periods, is_stationary):
    print(time, stationary)

120 True
140 True
160 True
180 True
200 True
220 True
240 True
250 False

Ótimas notícias, o nosso par possui resíduo estacionário com 95% de confiabilidade em 7 dos 8 intervalos que escolhemos! Isso significa que o resíduo desse par pode ser considerado estacionário segundo os nossos critérios.

Podemos também plotar o resíduo para visualizar essa estacionariedade. Para isso, precisamos primeiramente chamar a função calculate_residual com o intervalo de tempo que queremos observar.

df, beta = calculate_residual(stocks_train, 250)
df

	Base Asset	Comparison Asset	Residual
datetime
2020-05-08	3.44	30.45	-1.860236
2020-05-11	3.29	29.38	-1.790458
2020-05-12	3.23	29.72	-1.920294
2020-05-13	3.20	28.55	-1.709976
2020-05-14	3.40	29.92	-1.791374
...	...	...	...
2021-05-05	6.90	37.45	0.161964
2021-05-06	6.91	37.83	0.093912
2021-05-07	7.09	39.41	-0.050620
2021-05-10	6.86	39.71	-0.342240
2021-05-11	6.89	40.27	-0.427264

250 rows × 3 columns

Agora podemos plotar o resíduo juntamente com a média para esse intervalo.

mean = df['Residual'].mean()
    
plt.title("Residual for t = 250")
df['Residual'].plot(x="Major", y="", figsize=(14,6))
plt.axhline(y=mean, color='y', linestyle='-')   
plt.show()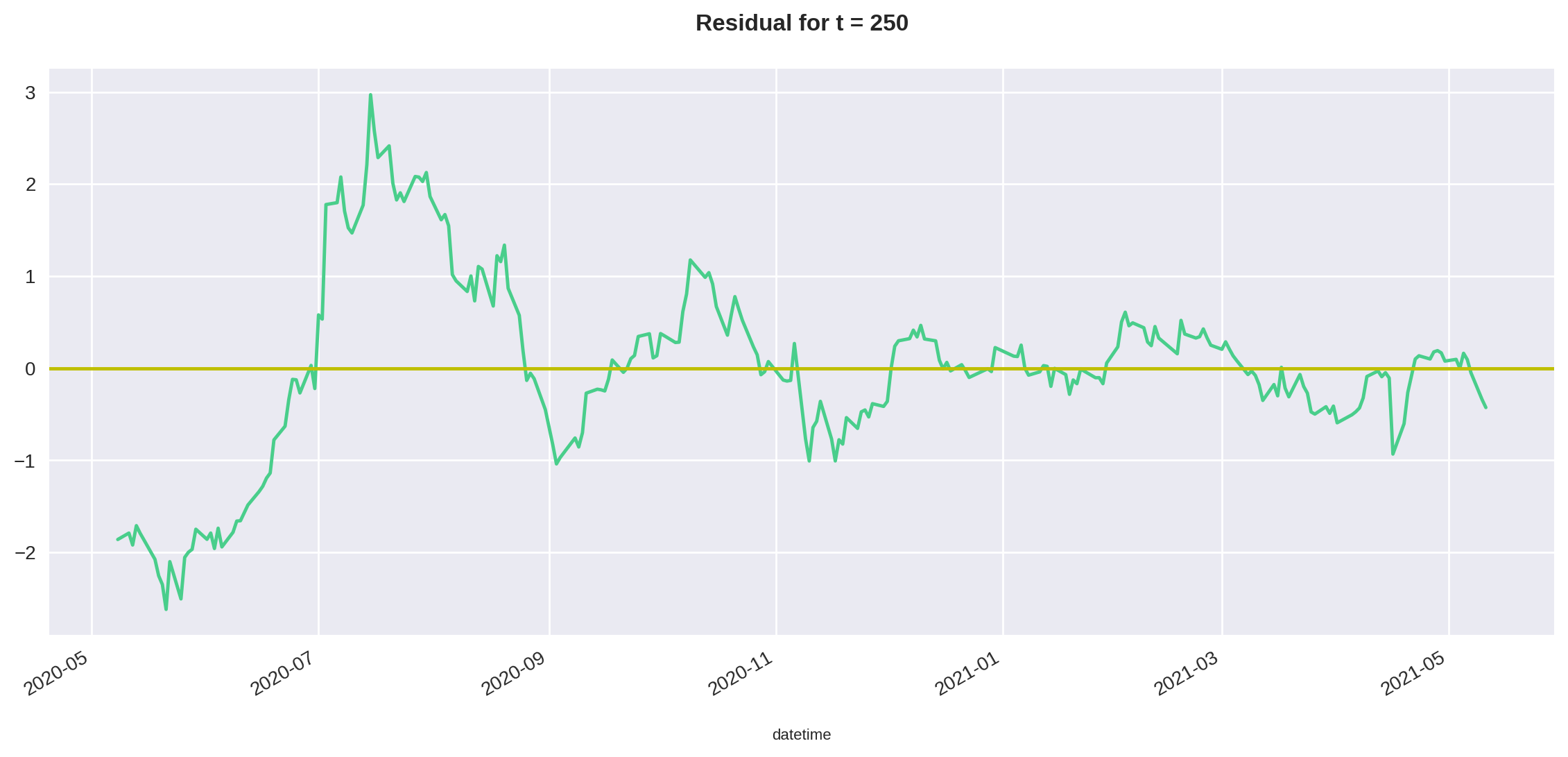

Embora o resíduo não pareça estacionário nos primeiros meses de análise, de fato ele claramente oscila em torno da média (eixo y = 0 no gráfico) após esse período inicial.

Antes de darmos início à nossa fase de teste, precisamos definir nosso critério de entrada, saída e stop.

Pontos de entrada, alvo e stop

O conceito da estratégia de Long & Short por cointegração é o retorno à média no resíduo de um par cointegrado. Portanto, o que se faz é definir uma determinada distância da média considerada uma discrepância para um resíduo estacionário. Ou seja, o resíduo já se afastou muito da média, e como ele é estacionário, ele tenderia a voltar para média.

Usualmente se define o ponto de entrada quando o resíduo de um par estacionário estiver em uma distância de dois desvios padrão para cima ou para baixo da média.

E qual será o alvo? Ora, uma vez que a estratégia é baseada em retorno a média, o será quando o resíduo do par voltar para média (i.e. desvio padrão = 0).

E o nosso stop? Aqui também não existe uma resposta específica, mas já que estamos buscando um retorno de dois desvios padrão (entrada em 2 e saída em 0), podemos definir o stop como sendo a três desvios padrões da média. Em outras palavras, arriscamos 1 desvio padrão para ganharmos 2.

Z-Score

Já que estamos definindo a distância da média em função do desvio padrão, faz sentido analisarmos o resíduo em função do desvio padrão. Para isso, podemos utilizar o Z-Score.

O Z-Score é uma medida estatística que descreve a relação de um determinado valor com a média de um conjunto de valores. No nosso caso, ele pode ser ser calculado subtraindo da média do conjunto de pontos, o valor do resíduo em um determinado ponto, tudo isso normalizado pelo desvio padrão do conjunto. Matematicamente:

$\textit{Z-Score}(i) = \frac{\text{residual}(i) - \rm{med(residual)}}{\sigma(\text{residual})}$

Onde $\rm med$ é a média e $\sigma$ é o desvio padrão.

Podemos facilmente calcular o Z-Score utilizando pandas.

df['Z-Score'] = (df['Residual'] - df['Residual'].mean()) / df['Residual'].std()
df

	Base Asset	Comparison Asset	Residual	Z-Score
datetime
2020-05-08	3.44	30.45	-1.860236	-1.887201
2020-05-11	3.29	29.38	-1.790458	-1.816411
2020-05-12	3.23	29.72	-1.920294	-1.948129
2020-05-13	3.20	28.55	-1.709976	-1.734763
2020-05-14	3.40	29.92	-1.791374	-1.817341
...	...	...	...	...
2021-05-05	6.90	37.45	0.161964	0.164312
2021-05-06	6.91	37.83	0.093912	0.095274
2021-05-07	7.09	39.41	-0.050620	-0.051353
2021-05-10	6.86	39.71	-0.342240	-0.347201
2021-05-11	6.89	40.27	-0.427264	-0.433457

250 rows × 4 columns

Como vamos plotar os resultados do Z-Score novamente durante o período de teste, criarmos uma função para plotar o Z-Score junto com os pontos de entrada ( $\sigma = 2$ ) e stop ( $\sigma = 3$ ) que definimos anteriormente.

def plot_residual(df, time_period):

    df = df.iloc[-time_period:].copy()

    std  = df['Z-Score'].std()
    
    up = 2 * std
    down = -2 * std
    stop_up = 3 * std
    stop_down = -3 * std

    plt.title("Z-Score for t = %i" %time_period)
    df['Z-Score'].plot(x="Major", y="", figsize=(14,6))
    plt.axhline(y=0, color='y', linestyle='-')
    plt.axhline(y=up,   color='b', linestyle='-')
    plt.axhline(y=down, color='b', linestyle='-')
    plt.axhline(y=stop_up,   color='r', linestyle='-')
    plt.axhline(y=stop_down, color='r', linestyle='-')

plot_residual(df, 250)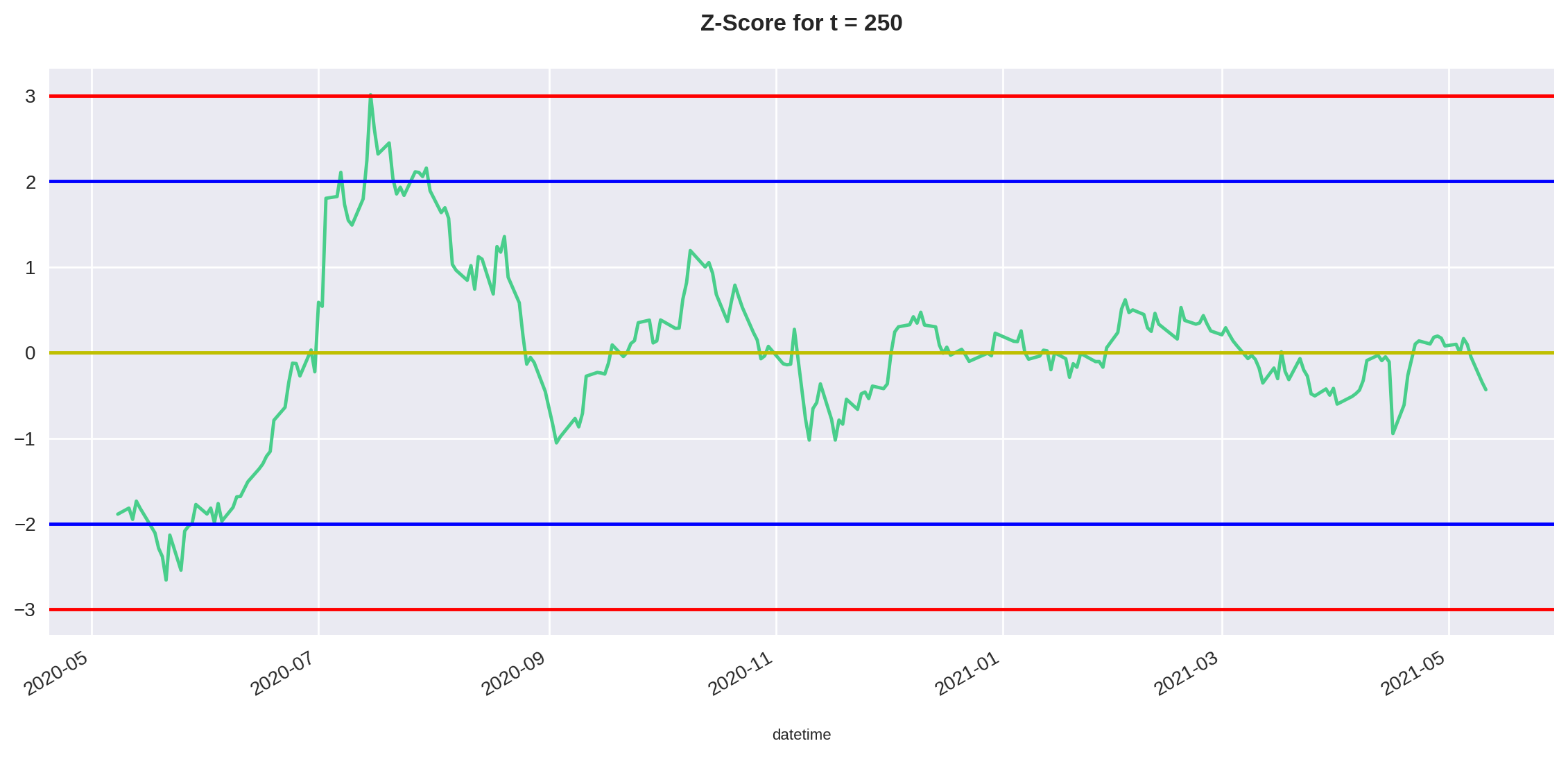

Note que qualitativamente o Z-Score se comporta igual ao resíduo. Porém repare que, agora, o eixo y possui valores relativos ao desvio padrão, o que facilita a nossa análise.

É importante ressaltar que nenhuma conclusão da estratégia pode ser tirada nesse ponto, uma vez que esse é apenas o conjunto de treino.

Proporção de compra e venda

A proporção de compra e venda vai depender do coeficiente angular (o nosso $\beta$ ) que obtemos treinando o nosso modelo linear. Nesse caso:

print('beta =', round(beta, 3))

beta = 0.205

O beta é de aproximadamente 0.20. Ou seja, para cada 1 ação do ativo base, nós vamos operar com 0.2 ações do ativo de comparação. Trazendo isso para a realidade dos lotes da bolsa, para cada 500 ações do ativo base, nós vamos operar 100 ações do ativo de comparação.

E qual ativo comprar e qual ativo vender?

Isso vai depender do valor do Z-Score. Como definimos 2 desvios padrão como sendo o nosso ponto de entrada, se o Z-Score for $\geq$ 2 nós vamos vender o ativo base e comprar o ativo de comparação.

Por outro lado, se o Z-Score for $\leq$ -2, nós vamos comprar o ativo base e vender o ativo de comparação. Sempre respeitando a proporção definida pelo beta.

Fase de teste

Agora que ja treinamos o modelo, definimos os pontos de entrada e saída, e aprendemos qual e quanto comprar ou vender de um determinado ativo, podemos dar início a fase de teste.

Ela será dividida nos seguintes passos:

Definir o dataframe com os dados de teste.
Calcular o novo resíduo, que será obtido como a diferença entre a variável depentente e o nosso modelo linear treinado anteriormente.
Calcular e plotar o Z-Score para análise de possíveis trades.

# define df as the dataframe holding the test data
df = stocks_test

# calculate the residual using the model obtained from the training set 
df['Residual'] = df.iloc[:,0] - beta * df.iloc[:,1]

# calculate Z-score
df['Z-Score'] = (df['Residual'] - df['Residual'].mean()) / df['Residual'].std()

df

	Base Asset	Comparison Asset	Residual	Z-Score
datetime
2021-05-12	6.78	39.07	-1.244978	-1.090657
2021-05-13	6.90	39.92	-1.299568	-1.258184
2021-05-14	6.97	39.58	-1.159732	-0.829052
2021-05-17	7.30	40.80	-1.080320	-0.585351
2021-05-18	7.32	40.44	-0.986376	-0.297053
...	...	...	...	...
2021-11-10	5.57	32.76	-1.158904	-0.826511
2021-11-11	5.65	33.93	-1.319222	-1.318499
2021-11-12	5.48	32.23	-1.140042	-0.768627
2021-11-16	5.18	31.21	-1.230534	-1.046331
2021-11-17	5.05	30.86	-1.288644	-1.224661

130 rows × 4 columns

Agora podemos chamar a função que criamos para plotar o Z-Score e analisar o resultado.

plot_residual(df, time_test)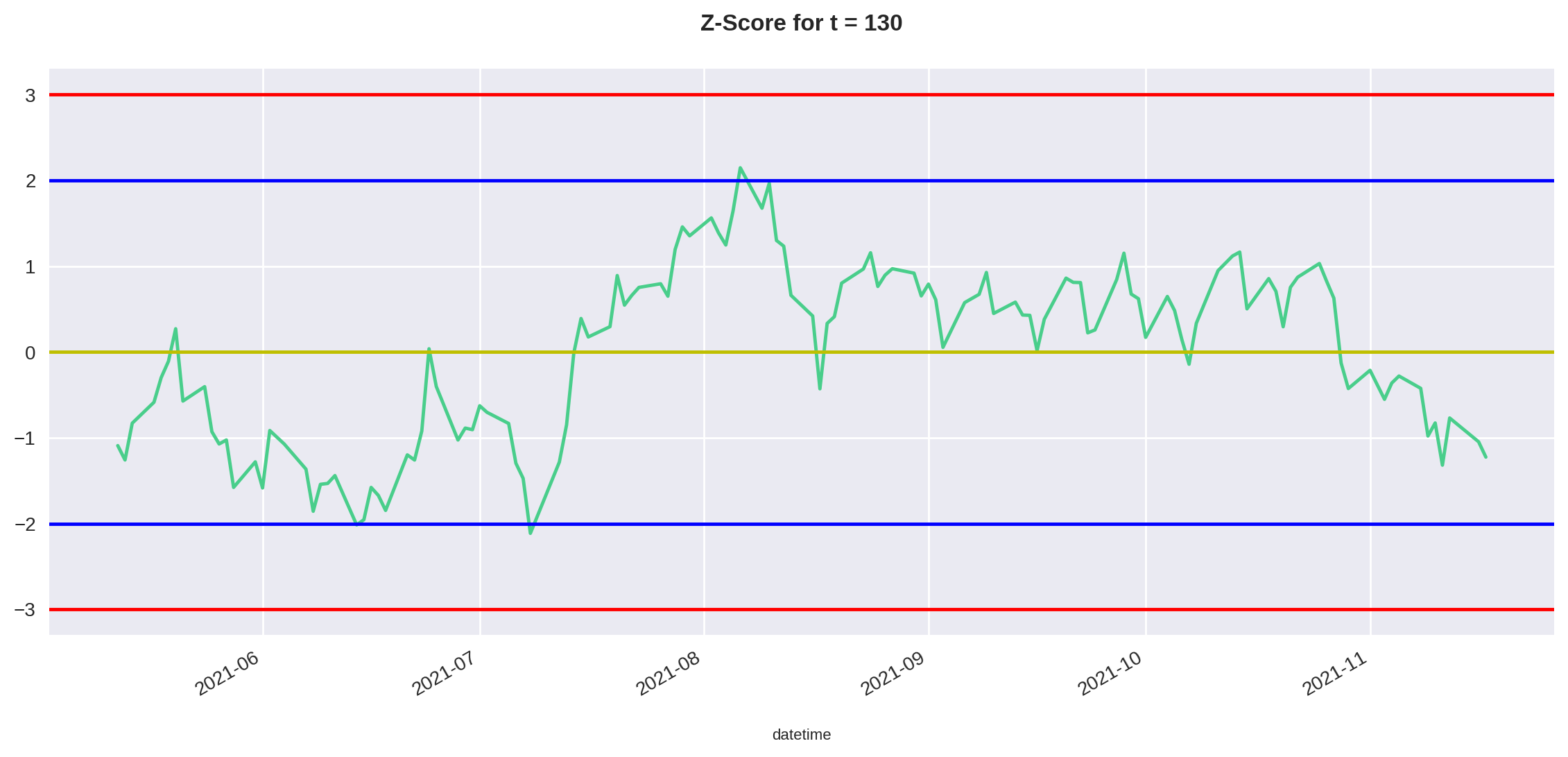

Como podemos ver no gráfico acima, nesse período de 130 dias a estratégia deu sinal de entrada três vezes.

Calcular cada um dos retornos para esse período deixaria esse post muito longo. Por isso, vamos deixar o cálculo exato do backtest para um próximo artigo.

Porém, podemos fazer uma análise mais qualitativa. Os dois primeiros trades aconteceraam na parte inferior do gráfico, onde o Z-Score estava menor que -2 (linha horizontal azul no gráfico).

Por isso, para esses dois primeiros trades seguiríamos a seguinte estratégia:

Compra de 500 unidades do ativo base (JHSF3) e venda de 100 unidades do ativo de comparação (LREN3).

Nesse caso, os dois trades teriam sido positivos, pois o Z-Score retornou a média.

Para o terceiro trade, o Z-Score chegou na ponta oposta do gráfico, em 2 desvios padrão positivo. Portanto, agora a estratégia muda de ordem. Nós iríamos:

Vender 500 unidades do ativo base (JHSF3) e comprar 100 unidades do ativo de comparação (LREN3).

Nesse caso, podemos ver no gráfico que o Z-Score também voltou à média e o trade teria sido positivo.

Conclusão e próximos passos

No artigo de hoje, demos sequência ao nosso estudo de cointegração onde aprendemos a criar um modelo linear, com base nos dados de treino, para podermos testar a nossa estratégia.

Definimos um intervalo de tempo com 8 janelas e aceitamos a cointegração do par se mais da metade dessas janelas possuíssem o resíduo estacionário. Além disso, escolhemos um período de 250 dias para ajustar o coeficiente do nosso modelo linear.

Aprendemos também a definir um ponto de entrada e stop com base no Z-Score.

Após, aplicamos o nosso modelo linear nos dados de teste, onde achamos três pontos de entrada. Todos eles teriam tido um retorno positivo, visto que o Z-Score retornou a média.

No próximo artigo da série, vamos aprender a calcular um stop no tempo, com base na meia-vida do resíduo. Além disso, vamos calcular os retorno propriamente e realizar o backtest dessa estratégia!

Não se esqueça de se cadastrar na nossa plataforma para ficar por dentro de todas as novidades que vemos trazendo, seja em questão de artigos ou de funcionalidades como alertas e backtest de estratégias.

Um abraço e até a próxima!

Ainda não é cadastrado? Crie sua conta e leia com conforto habilitando o modo noturno. É de graça!

Criar conta

Não leva nem 1 minuto!

Siga-nos no Instagram @quant_brasil

Receba diariamente novidades sobre a plataforma, dicas de análise quantitativa, sinais, backtests, estatísticas e muito mais!