Dando continuidade ao nosso post sobre Long & Short (L&S) pelo método da cointegração, hoje vamos focar na escolha e quantidade de intervalos necessários para prosseguir com a estratégia.
A importância da janela de tempo
No primeiro artigo da série, escolhemos um intervalo de 250 dias (número aproximado de pregões em 1 ano), e aprendemos como calcular o resíduo de um par e como checar se esse resíduo é estacionário no tempo. Contudo, algumas perguntas não foram respondidas:
Por que essa escolha? E se escolhermos janelas de tempo diferentes?
Antes de respondê-las, vamos primeiro facilitar a nossa vida e programar uma função que executa os procedimentos que aprendemos no último post para qualquer janela de tempo.
Calculando a estacionariedade em diferentes intervalos
Vamos então analisar o par PETR3 e PETR4 que vimos ter o resíduo estacionário para o intervalo de 250 dias. Será que o resíduo desse par também será estacionário em outros intervalos?
O primeiro passo é importar as bibliotecas necessárias.
%%capture
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from statsmodels.tsa.stattools import adfuller
!pip install yfinance
import yfinance as yfE seguimos novamente pegando o dataframe com o tamanho de intervalo máximo, 250 dias.
start_date = "2018-02-27"
end_date = "2019-03-02"
stock1 = "PETR3.SA"
stock2 = "PETR4.SA"
df = yf.download([stock1, stock2], start = start_date, end = end_date)["Adj Close"]
df.columns=['PETR3','PETR4']
df
[*********************100%***********************] 2 of 2 completed
| PETR3 | PETR4 | |
|---|---|---|
| Date | ||
| 2018-02-27 | 20.965944 | 19.296173 |
| 2018-02-28 | 20.993145 | 19.260275 |
| 2018-03-01 | 20.648556 | 18.874352 |
| 2018-03-02 | 21.020350 | 19.305149 |
| 2018-03-05 | 21.618858 | 19.852625 |
| ... | ... | ... |
| 2019-02-25 | 27.928782 | 24.998383 |
| 2019-02-26 | 27.937939 | 24.886030 |
| 2019-02-27 | 28.084452 | 25.354166 |
| 2019-02-28 | 27.342735 | 25.335438 |
| 2019-03-01 | 26.738375 | 24.998383 |
250 rows × 2 columns
Agora podemos programar duas funções com base no primeiro artigo para automatizar esse processo.
A primeira função será chamada de calculate_residual e terá apenas dois parâmetros de entrada:
- o dataframe,
df; - o período de tempo que queremos calcular o resíduo,
time_period.
Essa função irá retornar o resíduo na forma de uma Series.
def calculate_residual(df, time_period):
# values converted into a numpy array
# '-1' to calculate the dimension of rows, and '1' to have only 1 column
X_independent = df.iloc[-time_period:,1].values.reshape(-1, 1)
Y_dependent = df.iloc[-time_period:,0].values.reshape(-1, 1)
# performing the linear regression
reg = LinearRegression().fit(X_independent, Y_dependent)
# get the predicted Y given X from the model
Y_predict = reg.predict(X_independent)
# attaching the residual (Y_dependent-Y_predict) from a numpy array to a pandas series
residual = pd.DataFrame(np.array(Y_dependent - Y_predict), columns=['Residual'])
return residualA segunda função será chamada de check_stationary e terá como parâmetros de entrada:
- o dataframe,
df; - uma lista com os períodos de tempo que queremos testar,
time_periods; - a confiança mínima (em porcentagem) para que possamos assumir estacionariedade do resíduo (por padrão, 95%),
min_confidence.
O output dessa função será True se o resíduo for estacionário ou False caso contrário.
Nessa função, nós iremos chamar a função calculate_residual para calcular o resíduo em cada intervalo de tempo escolhido.
def check_stationary(df, time_periods, min_confidence=95):
# initialising an empty list that will receive the output
stationary_intervals = []
# loop over the list for all time periods
for t in time_periods:
# call the function to calculate the residuals
residual = calculate_residual(df,t)
# performing the Augmented Dickey-Fuller test in the residual
residual_test = adfuller(residual['Residual'])
# calculating the condidence in percentage from the p-value (index 1 of the output test)
confidence = 100 * (1 - residual_test[1])
# testing for stationarity given a threshold
if confidence >= min_confidence:
stationary_intervals.append(True)
else:
stationary_intervals.append(False)
# return the interval and if it is stationary
return stationary_intervalsAgora que já tempos nossas funções prontas, vamos verificar a estacionariedade no intervalo de 250 dias usado no post anterior. Lembre-se que a variável time_periods é uma lista.
time_periods = [250]
min_confidence = 95
is_stationary = check_stationary(df,time_periods,min_confidence)
is_stationary
[True]Ótimo, confirmamos que a série é estacionária para o período de 250 dias.
Com isso, podemos agora testar o resíduo do nosso par para períodos diferentes, por exemplo 120 dias, 140 dias, 180 dias, etc.
Para faciliar a visualização, utilizaremos a função zip para gerar tuplas com a verificação de estacionariedade para cada período.
time_periods = [120,140,160,180,200,220,240,250]
min_confidence = 95
is_stationary = check_stationary(df,time_periods,min_confidence)
for time, stationary in zip(time_periods, is_stationary):
print(time, stationary)120 False
140 False
160 False
180 True
200 True
220 True
240 True
250 True
Observe que, embora os 3 primeiros períodos de tempo escolhidos não tenham o resíduo estacionário, os últimos 5 períodos apresentam resíduo estacionário.
Para compararmos gráficamente um resíduo estacionário de outro não-estacionário, podemos rapidamente programar uma função para plotá-los.
def plot_residual(df,time_period):
# call the function to calculate the residuals
residual = calculate_residual(df,time_period)
mean = residual['Residual'].mean()
std = residual['Residual'].std()
k = 2 # Factor to shift the bands
up = mean + std * k
down = mean - std * k
plt.title("Residual for t = %i" %time_period)
residual['Residual'].plot(x="Major", y="", figsize=(14,6))
plt.axhline(y=mean, color='y', linestyle='-')
plt.axhline(y=up, color='b', linestyle='-')
plt.axhline(y=down, color='b', linestyle='-')plot_residual(df, 250)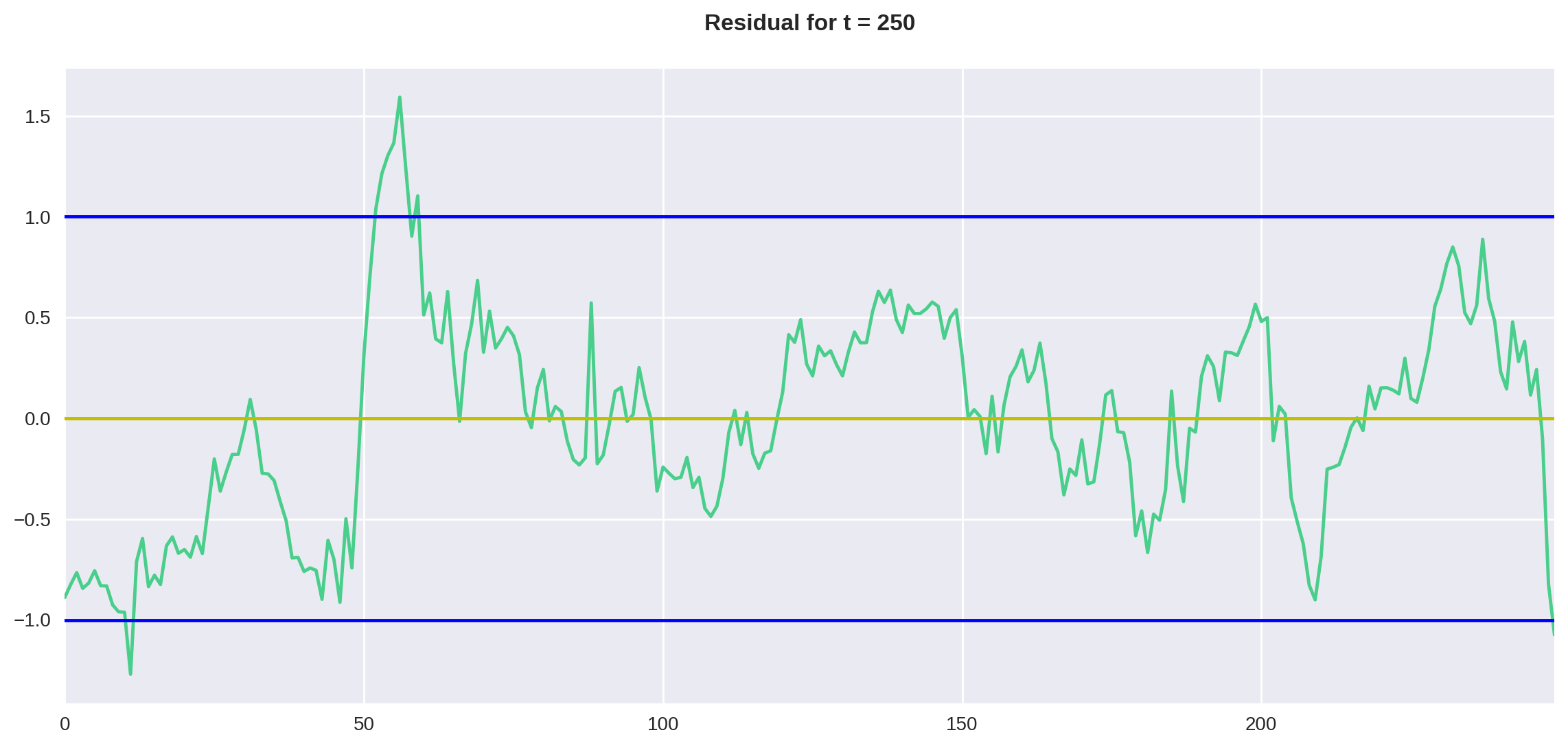
plot_residual(df, 140)
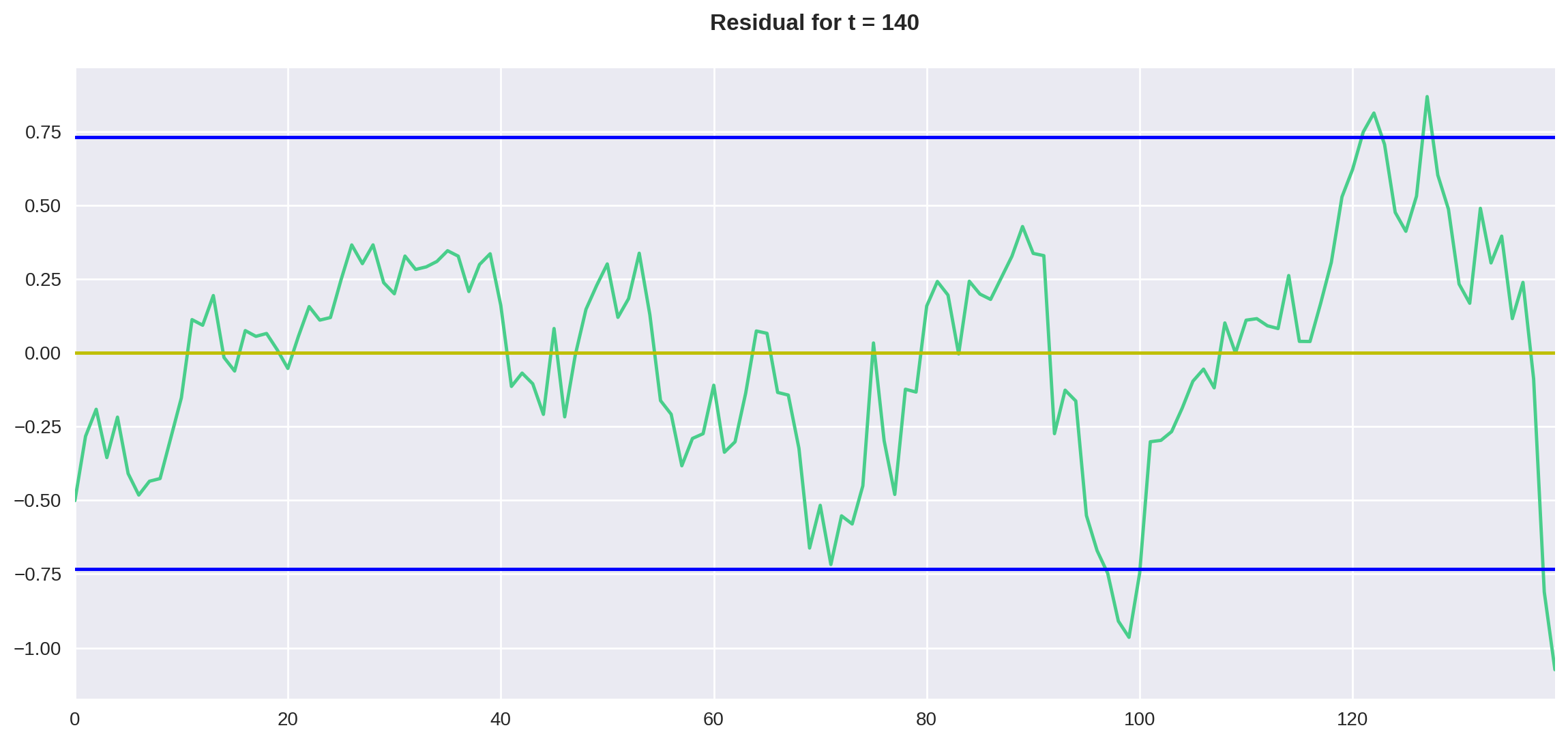
O que podemos perceber pelos gráficos é que, no período de 250 dias, o resíduo parece contido entre duas vezes o desvio padrão, diferentemente do período de 140 dias, onde o resíduo parece estar aumentando de amplitude com o tempo.
Escolhendo a janela de cointegração
Então se para períodos de tempo diferentes o resíduo pode ser ou não estacionário, o que me impede de escolher um ou outro para prosseguir com a análise?
A resposta é simples. Nada! Não existe uma maneira específica de se escolher o intervalo de tempo. Porém, alguns critérios podem ser estabelecidos através de backtests. Por exemplo:
- Escolhemos um período de 250 dias como o nosso critério para cointegração. Se a série estiver cointegrada, definimos um período de trade, onde tentaremos capitalizar com a possiblidade do retorno do resíduo a média. Ao término do período de trade, recalibramos o nosso modelo, ou seja, testamos novamente a cointegração para os últimos 250 dias. Se a cointegração persistir, continuamos com um novo período de trade. Se não, podemos esperar até o resíduo cointegrar novamente.
- Um critério mais rigoroso seria definir um número específico de intervalos estacionários dentro de uma janela de tempo para aceitarmos a cointegração. Por exemplo, podemos definir 8 intervalos de tempo (120, 140, 160, 180, 200, 220, 240, 250) e ter como critério que pelo menos 3 desses intervalos devem ser ser estacionários.
A função a seguir pode ser utilizada para implementar a estratégia 2:
def check_cointegration(check_stationary, min_periods=3):
# counting the number of True booleans in a list
number_of_trues = sum(check_stationary)
# condition to be cointegrate
if number_of_trues >= min_periods:
return True
else:
return Falsecheck_cointegration(is_stationary)TrueNesse caso, como o resíduo é estacionário para pelo menos 3 dos intervalos escolhidos, podemos dizer que o par PETR3 e PETR4 está cointegrado baseado nesse critério.
Próximos passos
Nesse post aprendemos como criar uma função para calcular o resíduo e definir se um par está cointegrado baseado na quantidade de resíduos estacionários em um determinado período de tempo.
Automatizando esse processo, podemos agora facilmente identificar se pares de ativos são cointegrados (escolhido um critério específico). Com isso, estamos prontos para executar nosso primeiro trade baseado na cointegração!
No próximo artigo da série, vamos aprender a identificar os sinais de entrada, estabelecendo assim nosso alvos e stops. Não deixe de se increver no nosso site e no grupo do Telegram para receber atualizações dos próximos artigos dessa série.
Um grande abraço e até a próxima!