Aprenda o que é ATR, Como Calculá-lo em Python e Exemplos Práticos de Suas Aplicações
No Mercado Financeiro, é muito importante entender a volatilidade de um ativo. Nós já exploramos alguns indicadores famosos de volatilidade, como as Bandas de Bollinger e o beta.
No artigo de hoje, vamos aprender um terceiro indicador, o ATR, e como podemos utilizá-lo de forma prática em nossas análises.
O que significa ATR?
ATR (sigla do inglês Average True Range) é um importante indicador da análise técnica, que foi primeiramente apresentado na literatura em 1978 por J. Welles Wilder Jr. em seu famoso livro New Concepts in Technical Trading Systems (o mesmo livro em que ele mostrou pela primeira vez o indicador IFR).
O seu significado pode ser compreendido pelo próprio nome: queremos obter uma média (average) dos valores de um determinado intervalo (range). Esse intervalo nada mais é do que o "tamanho", ou amplitude, do candle que você está analisando. Ou seja, você calcula o valor máximo e mínimo dos candles para um determinado intervalo e tira a média.
Contudo, em casos de gaps de alta ou baixa, a média da amplitude dos candles não é suficiente. É daí que vem o conceito de true range ou verdadeiro intervalo. Para esse indicador, os gaps também são levados em consideração.
Para exemplicar melhor esse conceito, considere os três casos da figura abaixo, adaptada do site Stockcharts.
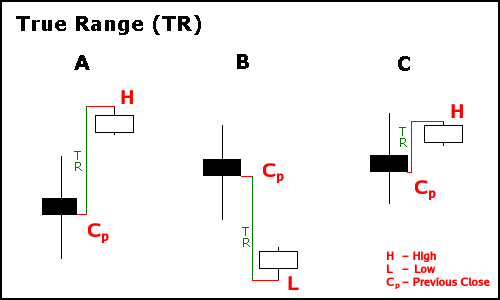
Para o caso A, o candle atual (em branco) possui uma pequena amplitude. Contudo, ele abriu com um gap de alta em relação ao candle anterior. Por isso, nesse caso o true range é calculado como a diferença entre o máximo do candle atual e o fechamento do candle anterior, que é maior que simplesmente calcular o valor do máximo e mínimo atual.
Para o caso B, a mesma coisa acontenceu em comparação ao caso A, porém com um gap de baixa. Nesse caso, o true range é calculado como a diferença entre o valor mínimo do candle atual e o valor de fechamento do candle anterior (não se preocupe, a gente vai pegar o valor absoluto, o valor negativo não importa).
Finalmente, no caso C, embora o gap seja menor, a amplitude do candle atual é bem pequena. Por isso, o true range é calculado para o maior valor, que nesse caso é a diferença entre o máximo do candle atual e o fechamento anterior.
Para que serve o ATR?
O ATR nos informa o grau de volatilidade de um ativo. Embora ele tenha sido originalmente desenvolvido para commodities devido a sua maior volatilidade, hoje em dia esse indicador é muito utilizado para qualquer tipo de ativo.
Existem duas formas principais em que esse indicador pode ser usado:
- Uma forma simples de identificar quando entrar ou sair de um trade baseado na volatilidade.
- Definir o tamanho das posições de cada ativo que deve-se comprar em um portfólio.
Normalmente, esse é um problema que podemos encontrar quando estamos montando o nosso portfólio. Utilizando o ATR, a proporção de cada ativo vai ser baseado na sua volatilidade, de forma a alocar o risco do seu portfólio de uma forma mais equilibrada.
Como calcular o ATR?
A matemática por trás do ATR é a seguinte: primeiramente temos que calcular o valor do true range, , para os primeiros candles (tipicamente, ). Esses candles podem ser em qualquer timeframe (intradiários, diários, semanais e até mensais).
O cálculo do true range se dá a partir da seguinte fórmula:
Onde é o valor máximo do candle, é o valor mínimo e é o valor de fechamento do candle anterior. Ou seja, estamos pegando o valor máximo dentre essas três opções. Após calcularmos o valor de para os primeiros nnn candles, nós podemos calcular o primeiro valor do aplicando a seguinte fórmula
Onde é o número de candles que queremos utilizar para nossa análise. Nesse caso, inicializamos o ATR com uma média aritmética simples do true range.
Agora que temos o primeiro valor do , podemos calcular os próximo valores usando a fórmula
para .
Em outras palavras, calculamos o ATR ponderando o valor anterior com o true range atual. Atribuímos o maior peso ao ATR anterior, que é exatamente a lógica utilizada no cálculo da média móvel exponencial.
Parece complicado? Calma que vamos análisar com calma no exemplo a seguir.
Calculando o ATR em Python
Vamos começar carregando as bibliotecas que vamos usar hoje.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt Para análise, vamos baixar os dados da JBS de 2019 até a data que esse artigo foi escrito. Esses dados estarão disponíveis no nosso grupo do telegram se você quiser repetir a análise feita nesse artigo mas fique à vontade para testar com seus próprios dados para os ativos que você queira analisar.
O tipo de dados que precisamos é o famoso OHLC (Open High Low Close) e aqui estaremos analisando no timeframe D1 (diário).
df = pd.read_csv('../data/D1/JBSS3-D1-OHLC-ATR.csv', index_col='datetime', parse_dates=True)
df
| open | high | low | close | |
|---|---|---|---|---|
| datetime | ||||
| 2019-01-02 | 11.58 | 12.04 | 11.38 | 12.04 |
| 2019-01-03 | 11.85 | 12.23 | 11.84 | 12.23 |
| 2019-01-04 | 12.07 | 12.89 | 11.99 | 12.55 |
| 2019-01-07 | 12.57 | 12.67 | 12.02 | 12.11 |
| 2019-01-08 | 12.20 | 12.35 | 12.04 | 12.30 |
| ... | ... | ... | ... | ... |
| 2022-01-20 | 36.85 | 37.14 | 36.11 | 36.32 |
| 2022-01-21 | 36.23 | 36.82 | 35.83 | 36.31 |
| 2022-01-24 | 36.50 | 37.11 | 35.65 | 35.92 |
| 2022-01-25 | 35.74 | 36.27 | 35.47 | 36.14 |
| 2022-01-26 | 36.41 | 36.84 | 36.10 | 36.27 |
762 rows × 4 columns
O primeiro passo, que foi descrito anteriomente, é calcular as diferenças entre os valores máximos e mínimos do candle assim como a diferença dos valores máximos e mínimos do candle com o fechamento do candle anterior. Utilizamos a função shift(1) para pegar o valor anterior em um DataFrame.
df['H-L'] = df['high'] - df['low']
df['|H-Cp|'] = np.abs(df['high'] - df['close'].shift(1))
df['|L-Cp|'] = np.abs(df['low'] - df['close'].shift(1))
df
| open | high | low | close | H-L | |H-Cp| | |L-Cp| | |
|---|---|---|---|---|---|---|---|
| datetime | |||||||
| 2019-01-02 | 11.58 | 12.04 | 11.38 | 12.04 | 0.66 | NaN | NaN |
| 2019-01-03 | 11.85 | 12.23 | 11.84 | 12.23 | 0.39 | 0.19 | 0.20 |
| 2019-01-04 | 12.07 | 12.89 | 11.99 | 12.55 | 0.90 | 0.66 | 0.24 |
| 2019-01-07 | 12.57 | 12.67 | 12.02 | 12.11 | 0.65 | 0.12 | 0.53 |
| 2019-01-08 | 12.20 | 12.35 | 12.04 | 12.30 | 0.31 | 0.24 | 0.07 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 2022-01-20 | 36.85 | 37.14 | 36.11 | 36.32 | 1.03 | 0.53 | 0.50 |
| 2022-01-21 | 36.23 | 36.82 | 35.83 | 36.31 | 0.99 | 0.50 | 0.49 |
| 2022-01-24 | 36.50 | 37.11 | 35.65 | 35.92 | 1.46 | 0.80 | 0.66 |
| 2022-01-25 | 35.74 | 36.27 | 35.47 | 36.14 | 0.80 | 0.35 | 0.45 |
| 2022-01-26 | 36.41 | 36.84 | 36.10 | 36.27 | 0.74 | 0.70 | 0.04 |
762 rows × 7 columns
Agora podemos calcular o valor do true range, TR, como sendo o valor máximo entre essas três possiblidades. Aqui, utilizamos axis=1 para pegar o máximo dentre os valores de interesse em cada linha.
df['TR'] = df[["|H-Cp|", "H-L", "|L-Cp|"]].max(axis=1)
df
| open | high | low | close | H-L | |H-Cp| | |L-Cp| | TR | |
|---|---|---|---|---|---|---|---|---|
| datetime | ||||||||
| 2019-01-02 | 11.58 | 12.04 | 11.38 | 12.04 | 0.66 | NaN | NaN | 0.66 |
| 2019-01-03 | 11.85 | 12.23 | 11.84 | 12.23 | 0.39 | 0.19 | 0.20 | 0.39 |
| 2019-01-04 | 12.07 | 12.89 | 11.99 | 12.55 | 0.90 | 0.66 | 0.24 | 0.90 |
| 2019-01-07 | 12.57 | 12.67 | 12.02 | 12.11 | 0.65 | 0.12 | 0.53 | 0.65 |
| 2019-01-08 | 12.20 | 12.35 | 12.04 | 12.30 | 0.31 | 0.24 | 0.07 | 0.31 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2022-01-20 | 36.85 | 37.14 | 36.11 | 36.32 | 1.03 | 0.53 | 0.50 | 1.03 |
| 2022-01-21 | 36.23 | 36.82 | 35.83 | 36.31 | 0.99 | 0.50 | 0.49 | 0.99 |
| 2022-01-24 | 36.50 | 37.11 | 35.65 | 35.92 | 1.46 | 0.80 | 0.66 | 1.46 |
| 2022-01-25 | 35.74 | 36.27 | 35.47 | 36.14 | 0.80 | 0.35 | 0.45 | 0.80 |
| 2022-01-26 | 36.41 | 36.84 | 36.10 | 36.27 | 0.74 | 0.70 | 0.04 | 0.74 |
762 rows × 8 columns
Até agora nenhuma grande novidade. Para o último passo, que é calcular o valor do ATR em si, existem diferentes possibilidades.
Como o nosso objetivo é ser didáticos mas também ensinar como usar as ferramentas disponíveis em Python para reduzir o tamanho de linhas no código e prezar por eficiência, vamos mostrar como calcular o ATR em uma linha usando a função ewm.
Essa função é muito interessante e já utilizamos ela anteriormente em diversos artigos do QuantBrasil para o cálculo de médias móveis exponenciais. Olhando na documentação do Pandas, veremos que ela é exatamente o que precisamos para calcular o ATR.
Porém, para ela funcionar do jeito que queremos, temos que definir alguns parâmetros. Observem na documentação que, se passarmos o parâmetro adjust=False na função, temos exatamente a equação do ATR descrita acima. E comparando as duas, vimos que precisamos setar o valor de alpha como sendo .
Notem que precisamos inicializar o ATR utilizando a média móvel aritmética simples como visto. Faremos isso "quebrando" o DataFrame em 2: os nnn primeiros serão utilizados para cálculo do , e os restantes para o cálculo do resto do indicador. Por fim, "juntaremos" os dois pedaços novamente e aí sim aplicamos a função ewm.
n = 14
sma = df['TR'].rolling(window=n, min_periods=n).mean()[:n]
rest = df['TR'][n:]
df['ATR'] = pd.concat([sma, rest]).ewm(alpha=1/n, adjust=False).mean()
df.head(20)
| open | high | low | close | H-L | |H-Cp| | |L-Cp| | TR | ATR | |
|---|---|---|---|---|---|---|---|---|---|
| datetime | |||||||||
| 2019-01-02 | 11.58 | 12.04 | 11.38 | 12.04 | 0.66 | NaN | NaN | 0.66 | NaN |
| 2019-01-03 | 11.85 | 12.23 | 11.84 | 12.23 | 0.39 | 0.19 | 0.20 | 0.39 | NaN |
| 2019-01-04 | 12.07 | 12.89 | 11.99 | 12.55 | 0.90 | 0.66 | 0.24 | 0.90 | NaN |
| 2019-01-07 | 12.57 | 12.67 | 12.02 | 12.11 | 0.65 | 0.12 | 0.53 | 0.65 | NaN |
| 2019-01-08 | 12.20 | 12.35 | 12.04 | 12.30 | 0.31 | 0.24 | 0.07 | 0.31 | NaN |
| 2019-01-09 | 12.22 | 12.55 | 12.12 | 12.20 | 0.43 | 0.25 | 0.18 | 0.43 | NaN |
| 2019-01-10 | 12.27 | 12.32 | 11.93 | 12.16 | 0.39 | 0.12 | 0.27 | 0.39 | NaN |
| 2019-01-11 | 12.25 | 12.51 | 12.23 | 12.48 | 0.28 | 0.35 | 0.07 | 0.35 | NaN |
| 2019-01-14 | 12.58 | 12.71 | 12.50 | 12.69 | 0.21 | 0.23 | 0.02 | 0.23 | NaN |
| 2019-01-15 | 12.62 | 12.78 | 12.48 | 12.62 | 0.30 | 0.09 | 0.21 | 0.30 | NaN |
| 2019-01-16 | 12.66 | 13.15 | 12.58 | 13.15 | 0.57 | 0.53 | 0.04 | 0.57 | NaN |
| 2019-01-17 | 13.12 | 13.50 | 12.84 | 13.40 | 0.66 | 0.35 | 0.31 | 0.66 | NaN |
| 2019-01-18 | 13.36 | 13.81 | 13.26 | 13.53 | 0.55 | 0.41 | 0.14 | 0.55 | NaN |
| 2019-01-21 | 13.42 | 13.72 | 13.20 | 13.70 | 0.52 | 0.19 | 0.33 | 0.52 | 0.493571 |
| 2019-01-22 | 13.92 | 14.13 | 13.37 | 13.60 | 0.76 | 0.43 | 0.33 | 0.76 | 0.512602 |
| 2019-01-23 | 13.69 | 14.10 | 13.63 | 14.08 | 0.47 | 0.50 | 0.03 | 0.50 | 0.511702 |
| 2019-01-24 | 14.12 | 14.47 | 13.97 | 14.47 | 0.50 | 0.39 | 0.11 | 0.50 | 0.510866 |
| 2019-01-28 | 14.18 | 14.80 | 14.08 | 14.80 | 0.72 | 0.33 | 0.39 | 0.72 | 0.525804 |
| 2019-01-29 | 14.81 | 14.88 | 14.58 | 14.70 | 0.30 | 0.08 | 0.22 | 0.30 | 0.509675 |
| 2019-01-30 | 14.73 | 15.65 | 14.68 | 15.30 | 0.97 | 0.95 | 0.02 | 0.97 | 0.542556 |
Para facilitar nossa vida, vamos programar o cálculo do ATR em uma função que será utilizada em muitos artigos daqui pra frente.
Nela, escolhemos um padrão de n=14 se nenhum valor de n for dado, porém esse valor pode ser modificado quando chamamos a função.
def calculate_atr(df,n=14):
#calculate the difference between candles
df['H-L'] = df['high'] - df['low']
df['|H-Cp|'] = np.abs(df['high'] - df['close'].shift(1))
df['|L-Cp|'] = np.abs(df['low'] - df['close'].shift(1))
# select the maximum value between the three possibilities to be our TR
df['TR'] = df[["|H-Cp|", "H-L","|L-Cp|"]].max(axis=1)
sma = df['TR'].rolling(window=n, min_periods=n).mean()[:n]
rest = df['TR'][n:]
df['ATR'] = pd.concat([sma, rest]).ewm(alpha=1/n, adjust=False).mean()
return dfPodemos também visualizar os valores calculados do ATR juntamente com o nosso gráfico de preço para usar como um poderoso indicador.
Para isso, construímos um subplot para mostrarmos os dois, um embaixo do outro, no mesmo gráfico.
# Plot the stock price with the ATR value
fig, (ax1, ax2) = plt.subplots(
nrows=2,
sharex=True,
figsize=(18, 10),
gridspec_kw={'height_ratios': [3, 1]}
)
# Plot stock price
ax1.plot(df['close'], label='JBSS3')
ax1.legend()
# Plot ATR
ax2.plot(df['ATR'], label='ATR', color="#033660")
ax2.legend()
plt.show()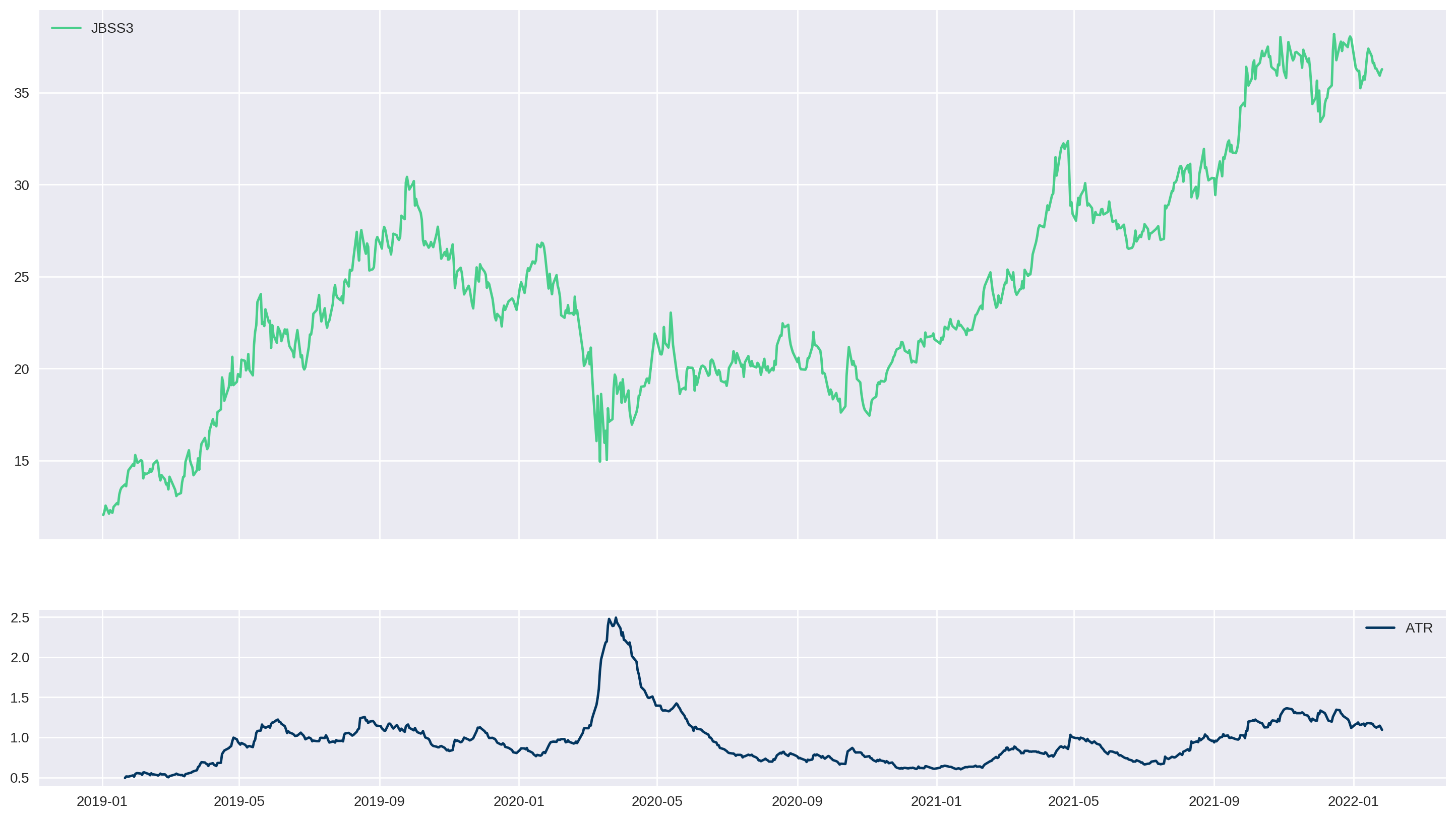
Vamos agora olhar dois exemplos práticos diferentes em que esse indicador pode ser utilizado. Primeiramente, vamos olhar a sua aplicação na análise gráfica.
Calculando o Canal de Keltner
O Canal de Keltner é muito parecido com suas primas famosas, as Bandas de Bollinger. A diferença é que usamos a média exponencial e ao invés de utilizar o desvio padrão para mover as médias para cima e para baixo, se utiliza o ATR. Por isso, esse canal também é baseado na volatilidade do ativo.
Normalmente, o período escolhido (span) para o cálculo é 20, embora modificações podem ser feitas dependendo da análise. Seguindo o mesmo padrão das Bandas de Bollinger, onde o desvio padrão era multiplicado por +/- 2 para mover as bandas, no canal de Keltner o ATR também é multiplicado por +/- 2 para formar o canal.
Para calculá-lo, o primeiro passo é gerar a média móvel exponencial para um período (span) de 20.
s = 20
df['EMA'] = df['close'].ewm(span=s).mean()
df.head()| open | high | low | close | H-L | |H-Cp| | |L-Cp| | TR | ATR | EMA | |
|---|---|---|---|---|---|---|---|---|---|---|
| datetime | ||||||||||
| 2019-01-02 | 11.58 | 12.04 | 11.38 | 12.04 | 0.66 | NaN | NaN | 0.66 | NaN | 12.040000 |
| 2019-01-03 | 11.85 | 12.23 | 11.84 | 12.23 | 0.39 | 0.19 | 0.20 | 0.39 | NaN | 12.139750 |
| 2019-01-04 | 12.07 | 12.89 | 11.99 | 12.55 | 0.90 | 0.66 | 0.24 | 0.90 | NaN | 12.290391 |
| 2019-01-07 | 12.57 | 12.67 | 12.02 | 12.11 | 0.65 | 0.12 | 0.53 | 0.65 | NaN | 12.238315 |
| 2019-01-08 | 12.20 | 12.35 | 12.04 | 12.30 | 0.31 | 0.24 | 0.07 | 0.31 | NaN | 12.253236 |
Por fim, criamos duas novas colunas no DataFrame para armazenar os valores superiores e inferiores do canal, criados a partir de um deslocamento da média exponencial em vezes o valor do ATR.
k = 2
df['Upper Channel'] = df['EMA'] + df['ATR'] * k
df['Lower Channel'] = df['EMA'] - df['ATR'] * k
df.tail()| open | high | low | close | H-L | |H-Cp| | |L-Cp| | TR | ATR | EMA | Upper Channel | Lower Channel | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| datetime | ||||||||||||
| 2022-01-20 | 36.85 | 37.14 | 36.11 | 36.32 | 1.03 | 0.53 | 0.50 | 1.03 | 1.130978 | 36.584930 | 38.846886 | 34.322974 |
| 2022-01-21 | 36.23 | 36.82 | 35.83 | 36.31 | 0.99 | 0.50 | 0.49 | 0.99 | 1.120908 | 36.558746 | 38.800563 | 34.316930 |
| 2022-01-24 | 36.50 | 37.11 | 35.65 | 35.92 | 1.46 | 0.80 | 0.66 | 1.46 | 1.145129 | 36.497913 | 38.788171 | 34.207655 |
| 2022-01-25 | 35.74 | 36.27 | 35.47 | 36.14 | 0.80 | 0.35 | 0.45 | 0.80 | 1.120477 | 36.463826 | 38.704780 | 34.222872 |
| 2022-01-26 | 36.41 | 36.84 | 36.10 | 36.27 | 0.74 | 0.70 | 0.04 | 0.74 | 1.093300 | 36.445367 | 38.631967 | 34.258767 |
Simples, não?!
Agora podemos visualizar o Canal de Keltner igual fizemos com as Bandas de Bollinger.
df['close'].plot(figsize=(14, 10))
df['Upper Channel'].plot(linewidth=1)
df['Lower Channel'].plot(linewidth=1, color="#033660")
df['EMA'].plot(linewidth=1, color="#033660", linestyle="dashed")
plt.show()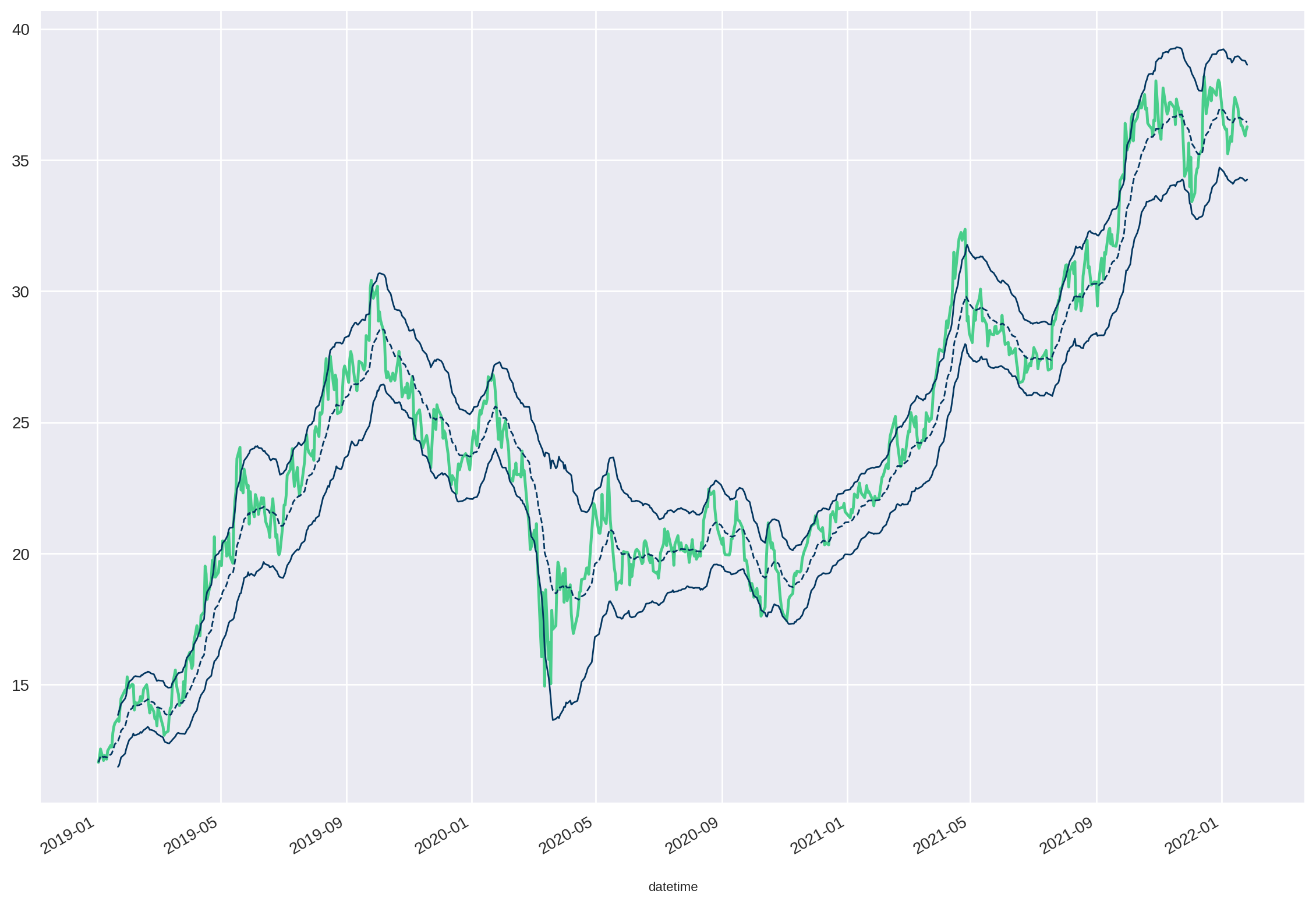
Podemos perceber claramente que o ativo está preso dentro do canal, e que nas poucas vezes que ele sai desse limite, ele tende a voltar para o canal. Além do mais, vemos uma forte tendência de retorno à média.
Definindo o tamanho de posições com o ATR
O ATR também pode ser utilizado para definir o tamanho das posições que devemos comprar de cada ativo em um portfólio. Já que o ATR é um indicador de volatilidade, podemos usá-lo para montar posições distribuindo o risco de forma a equilibrar o portfólio.
Isso se dá pois o risco alocado em comprar 1 real de um determinado ativo não é o mesmo que o risco em comprar 1 real de outro ativo — a volatilidade de cada ativo tem que ser levada em consideração. Na nossa lista de betas, por exemplo, fica claro que SUZB3 e TRAD3 tem volatilidade bem distintas.
Por isso, dentre várias fórmulas mais complicadas, existe uma simples que pode ser usada para definir o número de ações de um portfólio. Essa fórmula, que é função do ATR, pode ser escrita como:
Nessa fórmula, é o valor total que você quer alocar para montar seu portfólio e é um fator arbitrário que define o máximo impacto diário que uma ação pode ter no portfólio. Por exemplo, se esse valor é definido como , então você esta visando um impacto diário máximo de 0,1% no seu capital.
OBS: Dizemos impacto "diário" pois o ATR é tradicionalmente calculado nesse dia, mas a fórmula vale em qualquer timeframe.
Quanto menor você definir esse fator de risco, menor será o tamanho das posições para cada ação. Então cuidado quando for usar essa fórmula para não usar um fator muito baixo e encher seu portfólio de ativos e cair no mito da diversificação.
Exemplo prático
Vamos então calcular quanto compraríamos de JBS hoje se quiséssemos adicioná-la no nosso portfólio. Para isso, precisamos primeiramente definir nossas variáveis.
Suponha que temos um total de R$ 20.000 para investir e que aceitamos um risco máximo diário de 0.5%. Podemos descobrir o valor do ATR atual pegando o último dado do nosso df.
Aplicando isso na fórmula acima, obtemos:
total_capital = 20000
risk = 0.005
ATR = df['ATR'].iloc[-1]
shares = total_capital * risk / ATR
print(f'Número máximo de ações permitidas = {shares:.0f}')Número máximo de ações permitidas = 91
Ou seja, para o nosso valor de capital e o risco que escolhemos alocar, iriámos gastar:
current_price = df['close'].iloc[-1]
allowed_capital = shares * current_price
weight = allowed_capital / total_capital
print(f'Valor máximo permitido: R$ {allowed_capital:.2f}')
print(f'Máximo permitido equivalente a {weight:.2%} do capital')Valor máximo permitido: R$ 3317.48
Máximo permitido equivalente a 16.59% do capital
O principal ponto nesse caso é entender que, sempre que você estiver comprando posições de ativos para o seu portfólio, você está alocando risco e não dinheiro. A fórmula descrita acima nos possibilita olhar a volatilidade do ativo e definir o tamanho de nossa posição baseada nisso.
Conclusão
No artigo de hoje, aprendemos o que é e como calcular um importante indicador técnico, o ATR. Vimos também duas aplicações, seja para a análise técnica por meio do Canal de Keltner ou como uma forma de alocar as posições dos ativos no nosso portfólio baseando-se na volatilidade (position sizing).
Nos próximos artigos, utilizaremos o ATR como base fundamental numa estratégia de momentum. Para ficar por dentro de tudo que rola aqui no QuantBrasil, não se esqueça de criar uma conta no nosso site e entrar no nosso grupo do Telegram.
Um abraço!
Inscreva-se no canal do QuantBrasil!
Acompanhe novidades sobre a plataforma, vídeos sobre finanças quantitativas, tutoriais sobre programação e Inteligência Artificial!