Aprenda a Realizar o Backtest da Estratégia do Candle Pavio Utilizando Python
O padrão do Candle Pavio é definido pelo trader Stormer como um candle cujo corpo (diferença entre abertura e fechamento) apresenta tamanho menor ou igual a 20% de sua amplitude (diferença entre a máxima e a mínima).
Na plataforma do QuantBrasil, disponibilizamos um screening do Candle Pavio, que auxilia traders a identificarem esse padrão se formando nos timeframes diário e semanal.
Além disso, é possível rodar o backtest desse padrão no nosso Simulador de Estratégias. Hoje, entenderemos como esta estratégia funciona e como qualquer um pode realizar sua própria análise do Candle Pavio utilizando Python.
Entendendo a Estratégia do Candle Pavio
A ideia do Candle Pavio é identificar um momento de pré-explosão (daí o nome pavio) que pode ser representado por uma contração de volatilidade dos preços do ativo. Essa contração funciona como uma mola comprimida, que, uma vez que é "solta", seja para baixo ou para cima, poderá "explodir" nessa direção.
Dessa forma, para ativar a estratégia precisamos identificar duas condições:
- Uma contração de volatilidade. Representamos essa contração como um candle de corpo pequeno, ou seja, cujo tamanho da diferença entre a abertura e o fechamento tenha até 20% da amplitude total do candle (diferença entre a máxima e a mínima).
- Um rompimento dessa contração. O rompimento pode ser para baixo (operação de venda) ou para cima (operação de compra). Representamos esse rompimento como um gap de abertura.
Sendo essas duas condições satisfeitas, a operação é iniciada na abertura do candle e encerrada em seu fechamento. Note que embora isso signifique uma operação de day-trade no gráfico diário, essa estratégia pode ser utilizada no gráfico semanal (nesse caso, a entrada seria na abertura da segunda-feira e a saída no fechamento da sexta-feira).
Na nossa análise, faremos o backtest com os parâmetros mais usuais da estratégia:
- Timeframe diário;
- Corpo de até 20% da amplitude;
- Gap de pelo menos 0,5% em relação ao candle anterior.
Além disso, testaremos duas estratégias: uma sem stop e outra com stop a 2% do preço da abertura. Lembrando que os usuários do QuantBrasil podem customizar esses parâmetros no nosso Simulador de Estratégias.
Agora que já desmembramos a estratégia, vamos à análise!
Importanto as bibliotecas e os dados necessários
Como de costume, vamos importar as bibliotecas a serem utilizadas em nossa análise:
import pandas as pd
import numpy as np
import matplotlib.pyplot as pltEm seguida, vamos carregar a nossa base de dados, que estará disponível para download no nosso grupo do Telegram.
Realizaremos o backtest nos últimos 5 anos de negociações de PETR4.
df = pd.read_csv('../data/D1/PETR4-wick-candle.csv', index_col='datetime', parse_dates=['datetime'])
df
| open | high | low | close | |
|---|---|---|---|---|
| datetime | ||||
| 2017-01-06 | 15.72 | 15.86 | 15.45 | 15.61 |
| 2017-01-09 | 15.45 | 15.55 | 15.28 | 15.28 |
| 2017-01-10 | 15.55 | 15.63 | 15.34 | 15.43 |
| 2017-01-11 | 15.59 | 15.63 | 15.22 | 15.61 |
| 2017-01-12 | 16.08 | 16.18 | 15.84 | 15.84 |
| ... | ... | ... | ... | ... |
| 2021-12-29 | 28.70 | 28.90 | 28.42 | 28.54 |
| 2021-12-30 | 28.55 | 28.70 | 28.39 | 28.45 |
| 2022-01-03 | 28.54 | 29.22 | 28.53 | 29.09 |
| 2022-01-04 | 29.16 | 29.40 | 28.91 | 29.20 |
| 2022-01-05 | 29.19 | 29.27 | 28.41 | 28.41 |
1234 rows × 4 columns
Determinando os Sinais de Entrada
Com a base de dados em formato de dataframe, o primeiro passo para iniciarmos nossa análise é determinar os sinais de entrada. São eles: o candle pavio e a abertura em gap maior ou igual a 0,5%.
Como mencionado, o Candle Pavio (wick_candle) apresenta corpo (body) menor ou igual a 20% (body_pct) de sua amplitude (amplitude). Escreveremos o código da "perspectiva" do candle de entrada, portanto a primeira condição para entrarmos em uma operação é que o candle anterior seja um candle pavio (condition_1).
Em seguida determinaremos o gap, que caracteriza a diferença entre a abertura atual e o fechamento anterior. Nesse caso, essa diferença deve ser maior ou igual a 0,5% (gap_pct). Definimos então, nossa segunda condição de entrada (condition_2).
Como efeturaremos tanto operações de compra, como de venda, criaremos uma nova coluna signal a fim de separar os tipos de operações:
- Caso a abertura seja maior que o fechamento anterior (
long_condition), significa que houve um gap de alta e portanto a operação é de compra, ou seja,signalé1; - Caso contrário, o gap foi de baixa (
short_condition) e portanto a operação é de venda:signalé-1;
Se as condições para o Candle Pavio não acontecerem, não houve trade nesse dia e portanto signal é 0.
# Establishing the signal candle
# wick candle pattern: the candle body is less than or equal to 20% of the candle's amplitude
amplitude = df['high'] - df['low']
body = abs(df['open'] - df['close'])
body_pct = 0.2
wick_candle = body <= amplitude * body_pct
condition_1 = wick_candle.shift(1) == True
# The gap is the difference between the opening and the previous closing (in percent)
gap = abs(df['open'] - df['close'].shift(1)) / df['close'].shift(1)
gap_pct = 0.005
condition_2 = gap >= gap_pct
# Isolating buying operations (1) from selling (-1) operations according to conditions
long_condition = df['open'] > df['close'].shift(1)
short_condition = df['open'] < df['close'].shift(1)
df['signal'] = np.where(
condition_1 & condition_2 & long_condition, 1,
np.where(condition_1 & condition_2 & short_condition, -1, 0)
)
df
| open | high | low | close | signal | |
|---|---|---|---|---|---|
| datetime | |||||
| 2017-01-06 | 15.72 | 15.86 | 15.45 | 15.61 | 0 |
| 2017-01-09 | 15.45 | 15.55 | 15.28 | 15.28 | 0 |
| 2017-01-10 | 15.55 | 15.63 | 15.34 | 15.43 | 0 |
| 2017-01-11 | 15.59 | 15.63 | 15.22 | 15.61 | 0 |
| 2017-01-12 | 16.08 | 16.18 | 15.84 | 15.84 | 1 |
| ... | ... | ... | ... | ... | ... |
| 2021-12-29 | 28.70 | 28.90 | 28.42 | 28.54 | 0 |
| 2021-12-30 | 28.55 | 28.70 | 28.39 | 28.45 | 0 |
| 2022-01-03 | 28.54 | 29.22 | 28.53 | 29.09 | 0 |
| 2022-01-04 | 29.16 | 29.40 | 28.91 | 29.20 | 0 |
| 2022-01-05 | 29.19 | 29.27 | 28.41 | 28.41 | 0 |
1234 rows × 5 columns
OBS: Caso você tenha tido dificuldade em entender esse código, recomendo a leitura dos artigos mais antigos do nosso blog. Lá, temos posts bem introdutórios sobre pandas e NumPy.
Agora que temos um DataFrame com os sinais de compra e venda, podemos facilmente verificar quantos trades de cada tipo aconteceram no período:
# A trade happened whenever signal was different than 0
total_trades = df[df['signal'] != 0]
# Long trades have signal equal to 1, and short trades have signal equal to -1
long_trades = df[df["signal"] == 1]
short_trades = df[df["signal"] == -1]
print(f"Total de Operações: {len(total_trades)}")
print(f"Total de Operações de Compra: {len(long_trades)}")
print(f"Total de Operações de Venda: {len(short_trades)}")Total de Operações: 149
Total de Operações de Compra: 87
Total de Operações de Venda: 62
Aplicando os filtros acima, observamos um total de 149 operações baseadas nessa estratégia em 5 anos, das quais 87 foram de compra e 62 de venda. Isso resulta entre 2 a 3 trades por mês em média, o que configura um sinal pouco frequente (pelo menos para este papel).
Calculando a Rentabilidade e Taxa de Acerto
Para podermos calcular a rentabilidade e da taxa de acerto dessa estratégia, vamos separar todos os trades efetuados em um novo DataFrame (trades) e calcular o número de ações que serão compradas a cada operação.
Repare que o preço de entrada (entry) nada mais é do que o preço de abertura e o alvo (target), o preço de fechamento.
Para calcularmos o número de ações (shares), alocaremos uma quantidade inicial de capital (initial_capital) e compraremos o máximo de lotes cheios (múltiplos de 100) que conseguirmos. Sendo assim, toda operação terá uma quantidade fixa de capital disponível.
# Isolating all trades into a dataframe
trades = df[df["signal"] != 0].copy()
# The entry is always made at the opening
trades['entry'] = trades['open']
trades['target'] = trades['close']
# Create a function to round any number to the smallest multiple of 100
import math
def round_down(x):
return int(math.floor(x / 100.0)) * 100
# The number of shares is how much it is possible to buy with the allocated initial capital
initial_capital = 100000
trades['shares'] = trades['entry'].apply(lambda price: round_down(initial_capital / price))
trades
| open | high | low | close | signal | entry | target | shares | |
|---|---|---|---|---|---|---|---|---|
| datetime | ||||||||
| 2017-01-12 | 16.08 | 16.18 | 15.84 | 15.84 | 1 | 16.08 | 15.84 | 6200 |
| 2017-01-24 | 16.05 | 16.36 | 15.91 | 15.97 | 1 | 16.05 | 15.97 | 6200 |
| 2017-01-26 | 16.08 | 16.12 | 15.74 | 15.74 | 1 | 16.08 | 15.74 | 6200 |
| 2017-02-01 | 15.21 | 15.36 | 14.86 | 14.97 | 1 | 15.21 | 14.97 | 6500 |
| 2017-02-17 | 15.68 | 15.84 | 15.55 | 15.56 | -1 | 15.68 | 15.56 | 6300 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2021-11-30 | 26.28 | 26.58 | 25.88 | 26.39 | -1 | 26.28 | 26.39 | 3800 |
| 2021-12-01 | 26.76 | 27.50 | 26.44 | 26.54 | 1 | 26.76 | 26.54 | 3700 |
| 2021-12-07 | 29.32 | 29.61 | 28.84 | 29.40 | 1 | 29.32 | 29.40 | 3400 |
| 2021-12-09 | 29.14 | 29.53 | 28.83 | 29.33 | -1 | 29.14 | 29.33 | 3400 |
| 2021-12-17 | 29.36 | 29.68 | 28.82 | 28.99 | -1 | 29.36 | 28.99 | 3400 |
149 rows × 8 columns
O resultado (result) de cada operação nada mais é do que a diferença entre a entrada e a saída, multiplicada pelo sinal da operação.
Já o lucro (profit) é o resultado multiplicado pelo número de ações compradas (shares). Podemos ainda calcular o lucro acumulado (acc_profit) a fim de plotarmos a evolução do nosso capital no período (utilizamos a função cumsum para isso).
trades['result'] = trades['signal'] * (trades['target'] - trades['entry'])
trades['profit'] = trades['shares'] * trades['result']
trades['acc_profit'] = trades['profit'].cumsum()
trades
| open | high | low | close | signal | entry | target | shares | result | profit | acc_profit | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| datetime | |||||||||||
| 2017-01-12 | 16.08 | 16.18 | 15.84 | 15.84 | 1 | 16.08 | 15.84 | 6200 | -0.24 | -1488.0 | -1488.0 |
| 2017-01-24 | 16.05 | 16.36 | 15.91 | 15.97 | 1 | 16.05 | 15.97 | 6200 | -0.08 | -496.0 | -1984.0 |
| 2017-01-26 | 16.08 | 16.12 | 15.74 | 15.74 | 1 | 16.08 | 15.74 | 6200 | -0.34 | -2108.0 | -4092.0 |
| 2017-02-01 | 15.21 | 15.36 | 14.86 | 14.97 | 1 | 15.21 | 14.97 | 6500 | -0.24 | -1560.0 | -5652.0 |
| 2017-02-17 | 15.68 | 15.84 | 15.55 | 15.56 | -1 | 15.68 | 15.56 | 6300 | 0.12 | 756.0 | -4896.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2021-11-30 | 26.28 | 26.58 | 25.88 | 26.39 | -1 | 26.28 | 26.39 | 3800 | -0.11 | -418.0 | 19251.0 |
| 2021-12-01 | 26.76 | 27.50 | 26.44 | 26.54 | 1 | 26.76 | 26.54 | 3700 | -0.22 | -814.0 | 18437.0 |
| 2021-12-07 | 29.32 | 29.61 | 28.84 | 29.40 | 1 | 29.32 | 29.40 | 3400 | 0.08 | 272.0 | 18709.0 |
| 2021-12-09 | 29.14 | 29.53 | 28.83 | 29.33 | -1 | 29.14 | 29.33 | 3400 | -0.19 | -646.0 | 18063.0 |
| 2021-12-17 | 29.36 | 29.68 | 28.82 | 28.99 | -1 | 29.36 | 28.99 | 3400 | 0.37 | 1258.0 | 19321.0 |
149 rows × 11 columns
Vamos agora definir uma função statistics para calcular algumas estatísticas importantes para a nossa análise, além de plotar a evolução do nosso lucro.
def statistics(trades):
shorts = trades[trades['signal'] == -1]
successful_shorts = len(shorts[shorts['result'] > 0])
longs = trades[trades['signal'] == 1]
successful_longs = len(longs[longs['result'] > 0])
total_profit = sum(trades['profit']) / initial_capital
longs_profit = sum(longs['profit']) / initial_capital
shorts_profit = sum(shorts['profit']) / initial_capital
print(f'Total trades: {len(trades)}')
print(f'Total longs: {len(longs)}')
print(f'Total shorts: {len(shorts)}')
print(f'Successful trades: {successful_longs + successful_shorts}')
print(f'Successful bullish trades: {successful_longs}')
print(f'Successful bearish trades: {successful_shorts}')
print(f'Total Accuracy (%): {(successful_longs + successful_shorts) / len(trades):.2%}')
print(f'Bullish Accuracy (%): {(successful_longs) / len(longs):.2%}')
print(f'Bearish Accuracy (%): {(successful_shorts) / len(shorts):.2%}')
print(f'Total profit: {total_profit:.2%}')
print(f'Bullish Profit (%): {longs_profit:.2%}')
print(f'Bearish Profit (%): {shorts_profit:.2%}')
plt.title('Resultado')
graph = trades['acc_profit'].plot()
return graphstatistics(trades)Total trades: 149
Total longs: 87
Total shorts: 62
Successful trades: 76
Successful bullish trades: 41
Successful bearish trades: 35
Total Accuracy (%): 51.01%
Bullish Accuracy (%): 47.13%
Bearish Accuracy (%): 56.45%
Total profit: 19.32%
Bullish Profit (%): -11.72%
Bearish Profit (%): 31.04%
<matplotlib.axes._subplots.AxesSubplot at 0x7fd678e3ea10>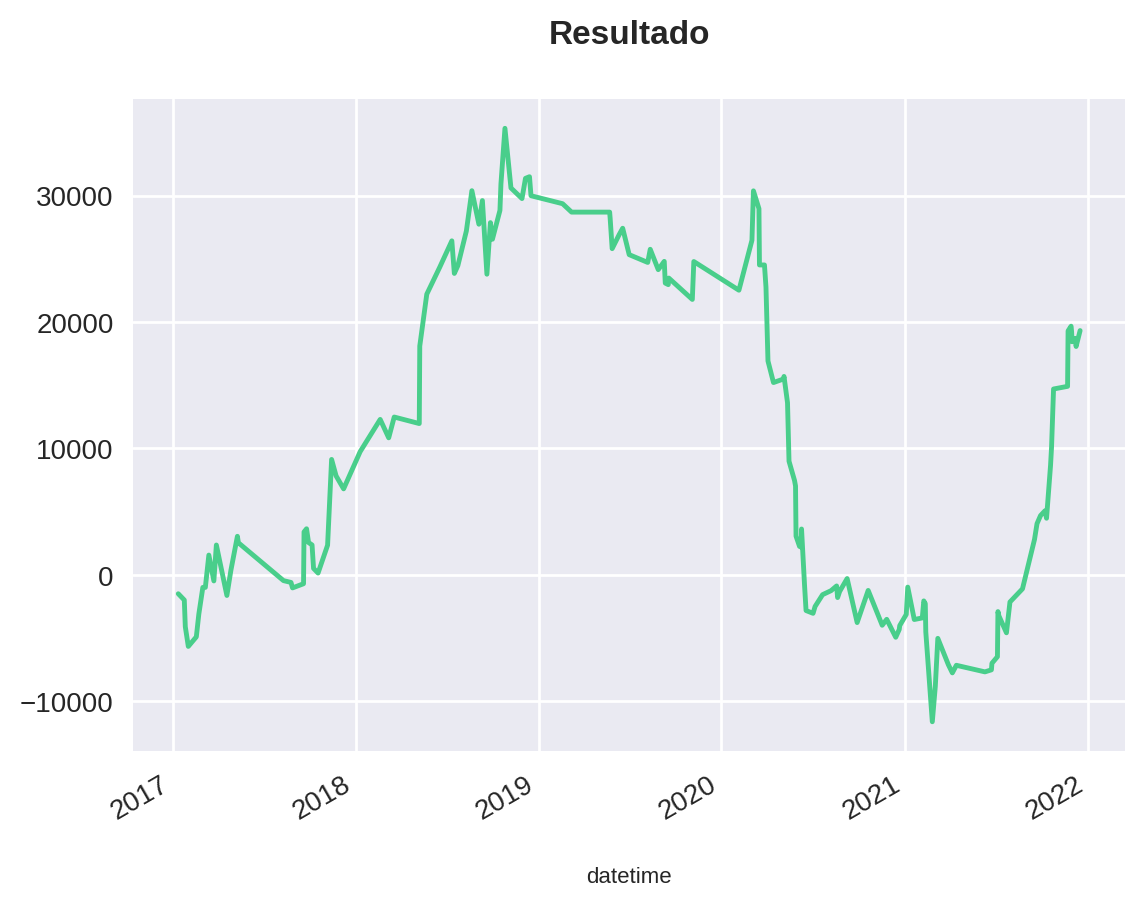
Analisando os dados acima, podemos dizer de uma maneira geral que os resultados não foram dos melhores: a taxa de acerto foi de 51% e o lucro de aproximadamente 19% em 4 anos.
Porém, se olharmos isoladamente para os trades efetuados na ponta da venda, vemos que os resultados foram mais promissores (taxa de acerto de 56% e lucro de 31%) do que aqueles operados na ponta da compra (taxa de acerto de 47% e lucro de -12%).
Além disso, através do gráfico nós podemos observar que a estratégia teve um ótimo desempenho em 2017 e 2018, ficou lateral em 2019, despencou em 2020 e se recuperou novamente em 2021. Essa queda brusca coincide com o período de pandemia da Covid-19, o que expõe as fragilidades de não se colocar nenhum stop.
Vamos tentar suavizar tal queda adicionando um stop calculado a partir de um risco fixo.
Aplicando um stop
A fim de limitar nossa perda quando uma operação falhar, vamos determinar um stop de 2% do nosso capital inicial (capital_exposure), ou seja, cada operação terá um risco máximo de R$2.000. O stop portanto, é determinado pelo preço de entrada multiplicado pelo risco estabelecido.
Para calculá-lo, faremos uma cópia do DataFrame atual (trades_w_stop). Em seguida, vamos diferenciar o stop das operações de compra e venda:
- No caso de uma compra, o stop fica abaixo do preço de entrada ;
- No caso de uma venda, o stop fica acima de entrada .
Portanto, para estabelecer o alvo, deveremos seguir a seguinte lógica:
- Caso seja uma operação de compra (sinal igual a 1) e a mínima for menor que o stop, significa que a operação foi stopada, logo o alvo será o stop calculado;
- Caso seja uma operação de venda (sinal igual a -1) e a máxima for maior que o stop, a operação também foi stopada;
- Se em ambos os casos o stop não for atingido, o alvo será o fechamento do candle.
trades_w_stop = trades[['entry', 'high', 'low', 'close', 'signal']].copy()
capital_exposure = 0.02
trades_w_stop['long_stop'] = round(trades_w_stop['entry'] * (1 - capital_exposure), 2)
trades_w_stop['short_stop'] = round(trades_w_stop['entry'] * (1 + capital_exposure), 2)
trades_w_stop['target'] = np.where(
(trades_w_stop['signal'] == 1) & (trades_w_stop['low'] < trades_w_stop['long_stop']),
trades_w_stop['long_stop'],
np.where(
(trades_w_stop['signal'] == -1) & (trades_w_stop['high'] > trades_w_stop['short_stop']),
trades_w_stop['short_stop'],
trades_w_stop['close']
)
)
trades_w_stop
| entry | high | low | close | signal | long_stop | short_stop | target | |
|---|---|---|---|---|---|---|---|---|
| datetime | ||||||||
| 2017-01-12 | 16.08 | 16.18 | 15.84 | 15.84 | 1 | 15.76 | 16.40 | 15.84 |
| 2017-01-24 | 16.05 | 16.36 | 15.91 | 15.97 | 1 | 15.73 | 16.37 | 15.97 |
| 2017-01-26 | 16.08 | 16.12 | 15.74 | 15.74 | 1 | 15.76 | 16.40 | 15.76 |
| 2017-02-01 | 15.21 | 15.36 | 14.86 | 14.97 | 1 | 14.91 | 15.51 | 14.91 |
| 2017-02-17 | 15.68 | 15.84 | 15.55 | 15.56 | -1 | 15.37 | 15.99 | 15.56 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2021-11-30 | 26.28 | 26.58 | 25.88 | 26.39 | -1 | 25.75 | 26.81 | 26.39 |
| 2021-12-01 | 26.76 | 27.50 | 26.44 | 26.54 | 1 | 26.22 | 27.30 | 26.54 |
| 2021-12-07 | 29.32 | 29.61 | 28.84 | 29.40 | 1 | 28.73 | 29.91 | 29.40 |
| 2021-12-09 | 29.14 | 29.53 | 28.83 | 29.33 | -1 | 28.56 | 29.72 | 29.33 |
| 2021-12-17 | 29.36 | 29.68 | 28.82 | 28.99 | -1 | 28.77 | 29.95 | 28.99 |
149 rows × 8 columns
Em seguida, vamos escrever uma função para calcular a quantidade de ações que negociaremos a cada operação (get_shares). Ela irá receber como argumentos: o capital inicial alocada para acada operação, o risco estabelecido, o preço de entrada e do stop.
Dividiremos essa função em 4 etapas:
- Calcular o risco máximo (
max_risk), que nós determinamos anteriormente que será de 2%; - Em seguida, calcularemos o risco inerente a cada operação (
operation_risk), que nada mais é do que a diferença entre a entrada e o stop; - A partir desses valores conseguimos descobrir quantas ações nós somos capazes de comprar com o capital alocado para cada operação, considerando o risco estabelecido (
allowed_shares); - Entretanto, só podemos negociar quantas ações o nosso capital alocado permitir (
max_shares). Sendo assim, sempre selecionaremos o mínimo entre a quantidade de ações que podemos adquirir de acordo com nosso risco e a quantidade de ações que podemos adquirir de acordo com nosso capital total.
def get_shares(initial_capital, capital_exposure, entry, stop):
# Maximum risk is how much of our initial capital we are willing to lose,
# where capital_exposure is the percentage of it
max_risk = initial_capital * capital_exposure
# The operation has an inherent risk: the difference between
# the price when we enter and the price when we are stopped (operation failed)
operation_risk = abs(entry - stop)
# Based on those two values, there is a max number of shares that we are allowed to buy
allowed_shares = max_risk / operation_risk
# But we can only buy as many shares as our initial capital allows
max_shares = initial_capital / entry
# Because of that, we will always buy the minimum between the number of shares we can buy
# according to our risk and the number of shares we can buy according to our capital
shares = min(allowed_shares, max_shares)
return round_down(shares)Como feito anteriormente, criaremos uma nova coluna shares para o número de ações adquiridas, aplicando get_shares ao longo do DataFrame através da função apply do pandas.
Por fim, calcularemos o resultado e o lucro novamente para, em seguida, calcular as estatísticas através da função statistics.
trades_w_stop['shares'] = trades_w_stop.apply(
lambda x: get_shares(
initial_capital,
capital_exposure,
x['entry'],
x['long_stop'] if x['signal'] == 1 else x['short_stop']
),
axis=1
)
trades_w_stop['result'] = trades_w_stop['signal'] * (trades_w_stop['target'] - trades_w_stop['entry'])
trades_w_stop['profit'] = trades_w_stop['shares'] * trades_w_stop['result']
trades_w_stop['acc_profit'] = trades_w_stop['profit'].cumsum()
# Delete unused columns
trades_w_stop.drop(['long_stop', 'short_stop'], axis=1, inplace=True)
trades_w_stop
| entry | high | low | close | signal | target | shares | result | profit | acc_profit | |
|---|---|---|---|---|---|---|---|---|---|---|
| datetime | ||||||||||
| 2017-01-12 | 16.08 | 16.18 | 15.84 | 15.84 | 1 | 15.84 | 6200 | -0.24 | -1488.0 | -1488.0 |
| 2017-01-24 | 16.05 | 16.36 | 15.91 | 15.97 | 1 | 15.97 | 6200 | -0.08 | -496.0 | -1984.0 |
| 2017-01-26 | 16.08 | 16.12 | 15.74 | 15.74 | 1 | 15.76 | 6200 | -0.32 | -1984.0 | -3968.0 |
| 2017-02-01 | 15.21 | 15.36 | 14.86 | 14.97 | 1 | 14.91 | 6500 | -0.30 | -1950.0 | -5918.0 |
| 2017-02-17 | 15.68 | 15.84 | 15.55 | 15.56 | -1 | 15.56 | 6300 | 0.12 | 756.0 | -5162.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2021-11-30 | 26.28 | 26.58 | 25.88 | 26.39 | -1 | 26.39 | 3700 | -0.11 | -407.0 | 33286.0 |
| 2021-12-01 | 26.76 | 27.50 | 26.44 | 26.54 | 1 | 26.54 | 3700 | -0.22 | -814.0 | 32472.0 |
| 2021-12-07 | 29.32 | 29.61 | 28.84 | 29.40 | 1 | 29.40 | 3300 | 0.08 | 264.0 | 32736.0 |
| 2021-12-09 | 29.14 | 29.53 | 28.83 | 29.33 | -1 | 29.33 | 3400 | -0.19 | -646.0 | 32090.0 |
| 2021-12-17 | 29.36 | 29.68 | 28.82 | 28.99 | -1 | 28.99 | 3300 | 0.37 | 1221.0 | 33311.0 |
149 rows × 10 columns
statistics(trades_w_stop)Total trades: 149
Total longs: 87
Total shorts: 62
Successful trades: 74
Successful bullish trades: 40
Successful bearish trades: 34
Total Accuracy (%): 49.66%
Bullish Accuracy (%): 45.98%
Bearish Accuracy (%): 54.84%
Total profit: 33.31%
Bullish Profit (%): 1.67%
Bearish Profit (%): 31.65%
<matplotlib.axes._subplots.AxesSubplot at 0x7fd678d9add0>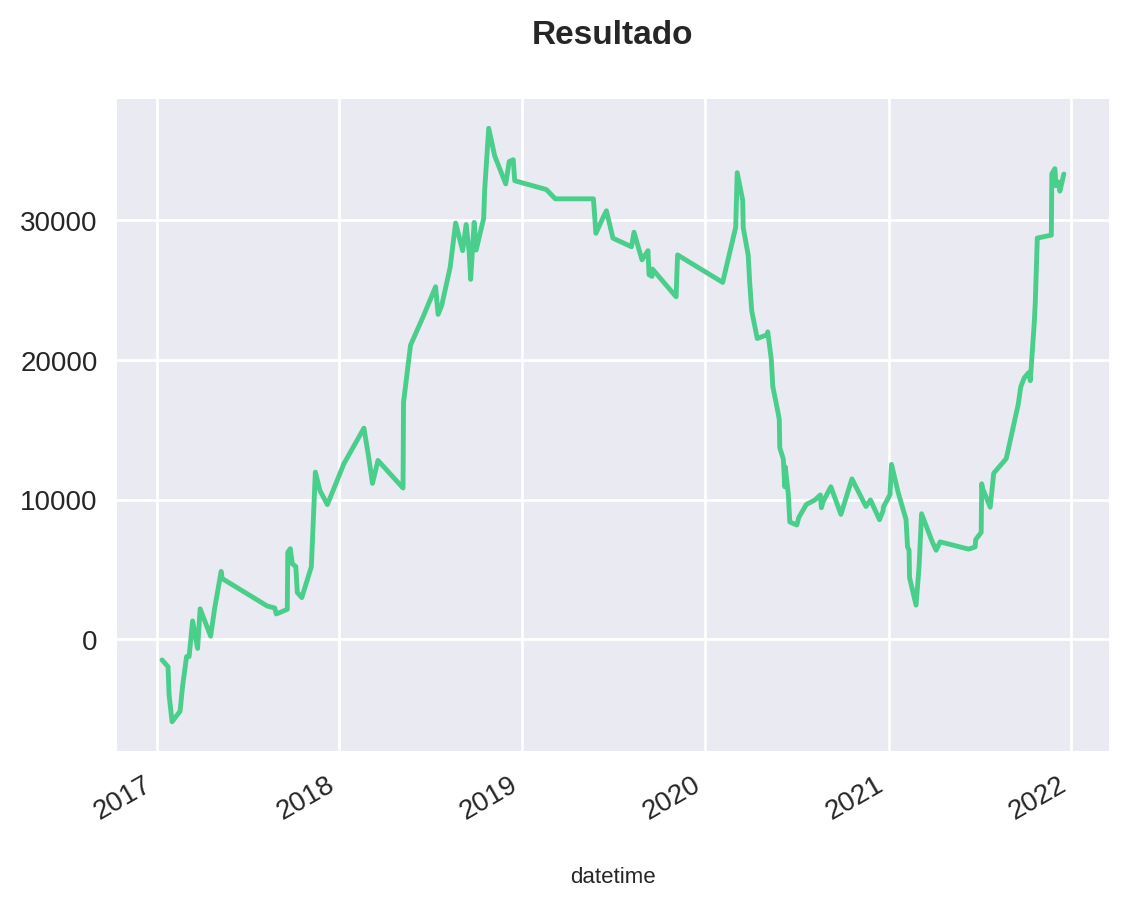
Podemos dizer que, ao aplicar o stop, nossa taxa de acerto manteve-se estável. Entretanto, nosso lucro saltou de 19% para 33%, muito influenciado pelas operações na ponta da compra, que reverteram um prejuízo de -12% para um pequeno lucro de 1%.
Embora o drawdown no 1º semestre de 2020 ainda tenha sido alto, conseguimos uma grande redução de prejuízo no período.
Conclusão
De uma maneira geral, podemos dizer que a estratégia do candle pavio demonstra um melhor desempenho em operações na ponta da venda do que operações de compra. Todavia, analisamos aqui apenas uma combinação de parâmetros que podemos aplicar para essa estratégia.
No Simulador de Estratégias, você pode alterar parâmetros como: timeframe, período, tamanho do corpo do candle pavio, tamanho do gap, quantidade de capital alocado para cada operação, risco, além de poder aplicar o Éden dos Traders como filtro.
Qualquer dúvida, basta mandar na caixinha de feedback localizada à sua direita (para membros) ou no nosso grupo do Telegram. Fique ligado porque o ano está só começando e temos muitas novidades por vir!
Inscreva-se no canal do QuantBrasil!
Acompanhe novidades sobre a plataforma, vídeos sobre finanças quantitativas, tutoriais sobre programação e Inteligência Artificial!