No artigo de hoje, vamos abordar um um fator importante ao nosso estudo sobre controle de risco ou risk management. Mas antes de começarmos, vamos entender um pouco mais sobre o que significa o controle de risco e qual a sua função em uma empresa (ou para você, investidor físico, que é o gerente do seu próprio portfólio).
Atualmente, a maioria dos fundos relacionados ao mercado financeiro possuem um setor de risk management. E esse setor é resposável por enviar informações cruciais para os gestores do fundo.
Uma função importante desse time é proteger o fundo de ficar exposto em grandes concentrações, evitando o aumento de risco do portfólio (lembra que a gente comentou no post sobre o ATR que ao investir em um ativo você está alocando risco e não dinheiro?).
Esse setor também é responsável por evitar surpresas — os riscos tomados devem ser sempre calculados. Nem poucos, dificultando o objetivo de alcançar retornos acima do seu benchmark, e nem muitos, que gerem perdas acima de um patamar considerado aceitável.
Em outras palavras, devemos estimar, com o maior número de informações possíveis, o quão ruim as coisas podem ir quando tudo der errado.
Controle de risco também pode ser aplicado para situações fora do mercado financeiro. Por exemplo, o grande piloto de fórmula 1 Nick Lauda uma vez disse:
"I accept every time I get in my car there’s a 20 percent chance I could die."
Ou seja, Nick concluiu que se o risco, baseado em suas análises sobre a pista, previsão do tempo e controle do carro, fosse maior que os 20% estimados, ele não participaria da corrida.
Então você pode estar se perguntando:
Mas como calculamos esse risco para um portfólio?
Ótima pergunta! Uma das forma mais usuais e simples de se estimar esse risco é conhecido como VaR, ou Value-at-Risk. E no artigo de hoje, vamos entender o seu significado, sua importância e aprender a calculá-lo em Python com um exemplo prático.
O que significa VaR?
VaR (sigla do inglês Value at Risk) é um valor estatístico usado para tentar quantificar a dimensão máxima de perdas que uma ação ou um portfólio pode sofrer em um determinado período de tempo. Por ser um metódo estatístico, o valor do VaR pode ser obtido para diferentes intervalos de confiança.
Como mencionado anteriormente, esse método de cálculo de risco é muito utilizado por risk managers para calcular e controlar o nível de exposição ao risco dos portfólios de suas empresas. Contudo, ele também pode ser aplicado para portfólios de pessoas físicas.
Instituições financeiras usam o VaR para determinar se os riscos estão maiores do que o esperado e, assim, reduzir a exposição em determinadas ações.
O VaR também pode ser usado em casos de alavancagem — uma determinada corretora pode utilizar o VaR para definir a margem total que deve ser depositada para uma determinada operação. Ou seja, usando os dados gerados pelo cálculo do VaR, pode-se determinar se existe reserva de dinheiro suficiente para cobrir eventuais perdas.
Exemplo de utilização do VaR
O VaR sempre deve estar atrelado a uma moeda, um intervalo de tempo e um determinado intervalo de confiança. Por isso, ele é normalmente utilizado da seguinte maneira:
"O nosso portfólio possui, com 95% de confiança, um VaR de R$10.000 para o próximo mês."
Em outras palavras, nós podemos afirmar com 95% de confiança que a perda máxima do nosso portfólio não será maior do que R$10.000 em um mês.
Como calcular o VaR?
Basicamente existem três formas de se calcular o VaR:
- Por meio de uma análise dos dados históricos;
- Por meio de uma simulação de Monte Carlo;
- Pelo método da variância-covariância.
No primeiro método, analisando-se dados históricos, ordena-se o retorno ao longo de um intervalo de tempo arbitrário. Daí, plota-se um histograma dos retornos e escolhe-se um intervalo de confiança.
O segundo método requer uma simulação de Monte Carlo. Por ser computacionalmente mais custoso, essa abordagem acaba sendo menos usando em comparação aos outros métodos. Fique ligado, porém, que iremos destrinchá-lo em um próximo artigo.
O terceiro método, variância-covariância, é o método que vamos explorar e aprender a calcular no artigo de hoje. Ele parte do suposto que os retornos de uma ação ou de um portfólio são distribuídos de acordo com uma curva normal. Dessa forma, conseguimos olhar para os piores casos existentes nessa curva. Vamos olhar esse caso em mais detalhes.
Entendendo o VaR pelo método da variância-covariância
Nesse método, assumimos que a curva de retornos de um determinado ativo ou portfólio se comporta de acordo com uma distribuição normal. Assim, os valores de potenciais perdas nos piores eventos podem ser obtidos dada à distância desses eventos da média.
A figura abaixo, obtida nesse paper, exemplifica visualmente o conceito do VaR por esse método.
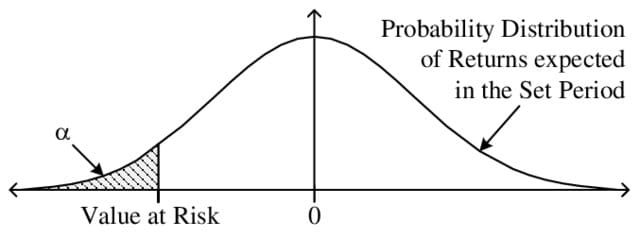
Como mencionando anteriormente, o VaR é atrelado a um certo intervalo de confiança (
Como consideramos que os valores se comportam segundo uma curva normal, ao final desse artigo, nós vamos colocar essa hipótese à prova e comparar os nossos resultados com uma curva normal para ver o quão perto (ou longe!) realmente estamos de um distribuição normal.
Aprenda a calcular o VaR em Python
Antes de começar o cálculo do VaR pelo método da variância-covariância, vamos primeiramente carregando as bibliotecas que iremos usar hoje.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import normVamos baixar os dados para uma carteira fictícia contendo as ações do Banco Inter, da JBS, da Petrobrás e da Vale para um período de 1 ano. Esses dados estarão disponíveis no nosso grupo do telegram mas fique à vontade para montar o seu portfólio usando os seus próprios dados.
Devido a forma que extraímos os dados do nosso banco usando SQL, precisamos usar a função pivot_table do pandas para organizar o nosso dataframe da maneira que queremos.
df = pd.read_csv('../data/D1/VaR-portfolio.csv', index_col='datetime', parse_dates=True)
df = df.pivot_table(index='datetime',columns='symbol',values='close')
df
| symbol | BIDI11 | JBSS3 | PETR4 | VALE3 |
|---|---|---|---|---|
| datetime | ||||
| 2021-02-11 | 48.97 | 24.17 | 22.96 | 79.25 |
| 2021-02-12 | 50.97 | 24.49 | 23.26 | 79.93 |
| 2021-02-17 | 50.59 | 25.23 | 24.20 | 82.02 |
| 2021-02-18 | 50.24 | 24.70 | 23.93 | 82.91 |
| 2021-02-19 | 53.02 | 24.20 | 22.35 | 83.23 |
| ... | ... | ... | ... | ... |
| 2022-02-04 | 23.37 | 34.24 | 32.63 | 87.98 |
| 2022-02-07 | 23.62 | 35.92 | 32.15 | 90.13 |
| 2022-02-08 | 25.54 | 37.58 | 31.83 | 91.39 |
| 2022-02-09 | 25.89 | 38.17 | 31.95 | 91.41 |
| 2022-02-10 | 24.82 | 38.24 | 32.44 | 93.87 |
249 rows × 4 columns
O próximo passo é calcular o retorno diário das ações que compõe o portfólio.
Já aprendemos em artigos anteriores que a vantagem de usar os valores do retorno ao invés do preço é a normalização: conseguimos estabelecer relações entre variáveis diferentes mesmo elas sendo originadas de séries temporais de diferentes ordens de magnitude.
Normalmente calculamos o retorno por meio da função pct_change. Contudo, para o artigo de hoje, vamos usar a variação logarítmica.
Existem algumas vantagens de se usar a variação logarítmica ao invés de simplesmente o retorno em si. A principal delas é a normalização log. Ou seja, se assumirmos que os preços estão distribuidos de forma log-normal (o que pode ou não ser verdade dependendo da série temporal), então o retorno log é convenientemente distribuído de acordo com uma curva normal. E você já consegue ter uma ideia de por que isso é importante para a gente no cálculo do VaR.
Para uma discussão mais detalhada sobre esse tipo de retorno, recomendo a leitura desse artigo.
returns = np.log(df / df.shift(1)).dropna()
returns
| symbol | BIDI11 | JBSS3 | PETR4 | VALE3 |
|---|---|---|---|---|
| datetime | ||||
| 2021-02-12 | 0.040029 | 0.013153 | 0.012982 | 0.008544 |
| 2021-02-17 | -0.007483 | 0.029769 | 0.039617 | 0.025812 |
| 2021-02-18 | -0.006942 | -0.021231 | -0.011220 | 0.010793 |
| 2021-02-19 | 0.053858 | -0.020451 | -0.068307 | 0.003852 |
| 2021-02-22 | -0.003022 | -0.037470 | -0.242342 | -0.025062 |
| ... | ... | ... | ... | ... |
| 2022-02-04 | -0.011910 | 0.010865 | 0.017311 | 0.025673 |
| 2022-02-07 | 0.010641 | 0.047900 | -0.014820 | 0.024144 |
| 2022-02-08 | 0.078152 | 0.045178 | -0.010003 | 0.013883 |
| 2022-02-09 | 0.013611 | 0.015578 | 0.003763 | 0.000219 |
| 2022-02-10 | -0.042207 | 0.001832 | 0.015220 | 0.026556 |
248 rows × 4 columns
Para deixar os cálculos mais realistas, vamos atribuir pesos para cada ação, já que raramente montamos um portfólio onde os ativos possuem proporções iguais. Lembre que quando estamos comprando uma ação estamos alocando risco e não dinheiro.
Vamos supor que para esse nosso portifólio temos os seguintes pesos: 20% de BIDI, 25% de JBS, 30% de PETR e 25% de VALE. Podemos então criar uma lista usando esses valores e transforma-la em um numpy array para podermos realizar operações matemáticas com ela.
weights = np.array([.2, .25, .3, .25])
weights
array([0.2 , 0.25, 0.3 , 0.25])Para cada dia temos que multiplicar os valores dos pesos pelos seus respectivos retornos e somá-los para calcular o retorno total diário do nosso portfólio.
Esse procedimento pode ser descrito na seguinte maneira matricial:
Onde
Para se realizar essa operação, poderimos contruir um loop para cada dia e ir somando os termos. Contudo, perceba que essa operação matemática nada mais é do que o produto interno. Por isso, podemos em uma linha de código calcular o retorno ponderado do nosso portfólio utilizando a função dot.
returns['portfolio'] = returns.dot(weights)
returns
| symbol | BIDI11 | JBSS3 | PETR4 | VALE3 | portfolio |
|---|---|---|---|---|---|
| datetime | |||||
| 2021-02-12 | 0.040029 | 0.013153 | 0.012982 | 0.008544 | 0.017324 |
| 2021-02-17 | -0.007483 | 0.029769 | 0.039617 | 0.025812 | 0.024284 |
| 2021-02-18 | -0.006942 | -0.021231 | -0.011220 | 0.010793 | -0.007364 |
| 2021-02-19 | 0.053858 | -0.020451 | -0.068307 | 0.003852 | -0.013870 |
| 2021-02-22 | -0.003022 | -0.037470 | -0.242342 | -0.025062 | -0.088940 |
| ... | ... | ... | ... | ... | ... |
| 2022-02-04 | -0.011910 | 0.010865 | 0.017311 | 0.025673 | 0.011946 |
| 2022-02-07 | 0.010641 | 0.047900 | -0.014820 | 0.024144 | 0.015693 |
| 2022-02-08 | 0.078152 | 0.045178 | -0.010003 | 0.013883 | 0.027395 |
| 2022-02-09 | 0.013611 | 0.015578 | 0.003763 | 0.000219 | 0.007800 |
| 2022-02-10 | -0.042207 | 0.001832 | 0.015220 | 0.026556 | 0.003222 |
248 rows × 5 columns
Agora podemos dar prosseguimento ao cálculo do VaR. Para isso, precisamos calcular a média e o desvio padrão dos valores do retorno do portfólio.
returns_mean = returns['portfolio'].mean()
returns_std = returns['portfolio'].std()
print(f'Portfolio daily returns mean = {returns_mean:.2%}')
print(f'Portfolio daily returns std = {returns_std:.2%}')Portfolio daily returns mean = 0.05%
Portfolio daily returns std = 1.79%
Com esse valores calculados, agora só precisamos usar a função norm.ppf da biblioteca de estatísticas do SciPy. O acrônimo ppf significa percent point function, que é outro nome dado para quantile function. Ou seja, essa função retorna, dado um intervalo de confiança, o valor crítico de uma determinada distribuição.
Por exemplo, considere que queremos determinar o valor crítico de 95% para um distribuição normal com média 0 e desvio padrão 1. Se você já teve e se lembra das aulas de estatística, vai saber que esse valor (chamado de z*) é de 1.64. Ou seja, dada uma distribuição normal com média em 0 e desvio padrão 1, 95% dos valores vão estar entre -1.64 e 1.64.
Esse valor pode ser calculado usando a função norm.ppf, que recebe primeiramente o intervalo de confiança, seguido da média e do desvio padrão.
norm.ppf(0.95, 0, 1)1.6448536269514722Agora podemos aplicar essa função para o nosso portfólio, que já calculamos a média e o desvio padrão.
Escolhendo então um intervalo de confiança de 95%, temos:
alpha = 0.05 # if 0.05, we are using: 1 - alpha = 0.95 or 95% confidence level
var = norm.ppf(alpha, returns_mean, returns_std)
print(f'The VaR value is {var:.2%} for our potfolio.')The VaR value is -2.89% for our potfolio.
Já que estamos interessados no pior caso, usamos
Pronto! Agora já calculamos qual é o valor do VaR diário para o nosso portfólio!
Com esse número, podemos afirmar o seguinte, dado um capital inicial investido na contrução do portfólio:
capital = 100000
max_losses = var*capital
print(f'We have {1-alpha:.0%} confidence that out selected portfolio of R${capital:.0f} invested will not exceed losses greater than R${max_losses:.2f} daily.')We have 95% confidence that out selected portfolio of R$100000 invested will not exceed losses greater than R$-2892.31 daily.
Comparando o retorno do portfólio com uma distribuição normal
Antes de terminar esse artigo, vamos de fato analisar se faz sentido assumir uma distribuição normal para o retorno do portfólio.
Para isso, considere o código abaixo, escrito para plotar um gráfico comparando os retornos do portfólio com uma distribuição normal que possui a mesma média e desvio padrão.
Vamos também marcar o valor do VaR que obtemos nesse gráfico.
O primeiro passo é plotar o histograma utilizando a função hist para a nossa série de retornos.
Depois, plotamos a distribuição normal utilizando a função pdf que calcula a probability density function.
Para esse cálculo, precisamos definir o nosso eixo x. Então, criamos uma vetor com 50 valores linearmente espaçado entre +/- 4 desvios padrão. Esse intervalo é suficiente para fins de visualização.
Por fim, adicionamos uma linha vertical no valor do VaR e adicionamos textos ao gráfico para identificarmos os dados.
# plot the histogram of the portfolio returns
returns['portfolio'].hist(bins=25, density=True, histtype='stepfilled', alpha=0.4, color='green')
# plot a theoretical normal distribution based on portfolio returns statistics
x = np.linspace((returns_mean - 4*returns_std), (returns_mean + 4*returns_std), 50)
plt.plot(x, norm.pdf(x, returns_mean, returns_std), 'r--', lw=2)
# add VaR value as a vertical line
plt.axvline(x=var, color = 'darkblue')
# add text to plot
plt.text(0.02, 15, 'normal distribution', fontsize=10, color='red')
plt.text(-0.02, 5, 'portfolio returns', fontsize=10, color='darkgreen')
plt.text(-0.042, 20, 'VaR', fontsize=11, color='darkblue')
# add label
plt.ylabel('Frequency')
plt.show()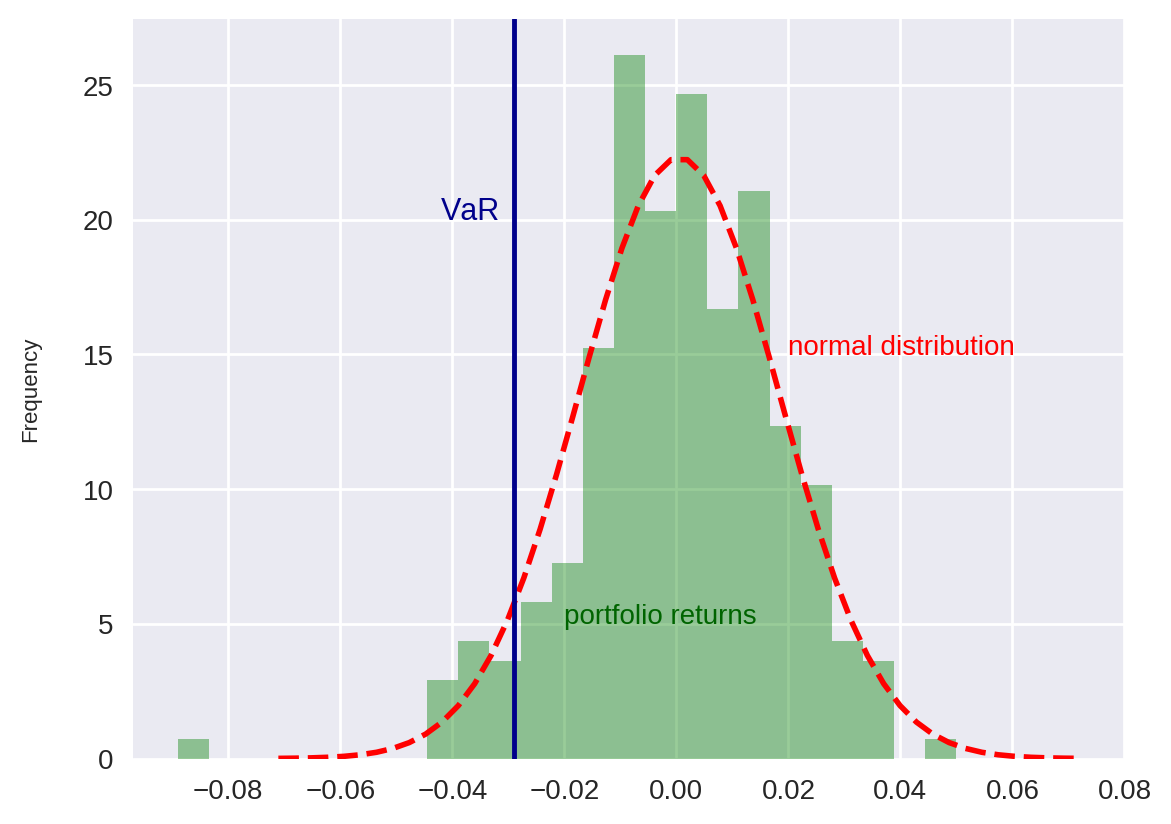
Note que os retornos do portfólio se comportam qualitativamente como uma função normal, com a maior parte dos seus valores perto da média e diminuindo a medida que aumentamos a distância dela.
Porém note que essa aproximação não é perfeita. De fato, podemos identificar no gráfico que houve alguns períodos onde a perda foi maior do que o esperado em uma distribuição normal. Isso se dá por conta do chamado efeito de cauda ou fat tail.
Ou seja, nas caudas as perdas são mais impactantes do que as calculadas por uma distribuição normal.
Conclusão
No artigo de hoje, entendemos os motivos pelo o qual o departamento de controle de risco de uma empresa é importante e algumas de suas missões.
Vimos que uma das maneiras utilizadas para estimar o risco de um portfólio é por meio do cálculo do VaR. Por isso, destrinchamos o seu significado, e mostramos exemplos de suas aplicações.
Aprendemos a calculá-lo de forma prática para um portfólio fictício que pode ser facilmente adaptado para receber os dados do seu próprio.
Por fim, comparamos os resultados obtidos com a hipótese que assumimos inicialmente de que os retornos do portfólio se comportam de acordo com uma curva normal, e vimos que de fato eles são parecidos. Contudo, devemos ficar atentos a possíveis efeitos de cauda (fat tails).
Os dados que utilizamos aqui hoje estarão disponíveis no nosso grupo do Telegram.
Não se esqueça de criar uma conta no nosso site para ficar por dentro de tudo que rola aqui no QuantBrasil!
Um abraço e até a próxima!