Backtest da Estratégia do Estocástico Lento em Python

No último artigo sobre o indicador Estocástico, aprendemos como calculá-lo e plotá-lo utilizando pandas e matplotlib. No artigo de hoje, daremos início a uma série de backtests com diferentes conjuntos de regras para a estratégia do Estocástico Lento.

A estratégia a ser testada hoje terá as seguintes características:

Timeframe: 120 minutos;
Tipo de operação: ponta da compra;
Ponto de entrada:
1. $\%K$ menor ou igual a um valor pré-definido (testaremos para 30, 25 e 20);
2. Candle seguinte fechando acima da abertura (candle sinal);
3. Média móvel exponencial de 80 períodos virada para cima;
4. Se as três condições acima forem respeitadas, a compra será efetuada no rompimento da máxima do candle sinal.
Stop loss: mínima do candle sinal.
Alvo: 2x o risco (diferença entre o ponto de entrada e o stop);

Agora que já definimos as regras de operação, vamos ao código!

Importando as bibliotecas e os dados necessários

Os timeframes intradiários da biblioteca do Yahoo Finance (que geralmente utilizamos em nossos backtests) são limitados e os preços ajustados apresentam algumas inconsistências. Dessa forma, utilizaremos outra fonte de dados: o MetaTrader.

Em um próximo post, aprenderemos a extrair os dados do MetaTrader e inseri-los em um banco de dados. De qualquer forma, o procedimento é simples e pode ser visto em Start Building Your Trading Strategies in 5 Minutes With Python and MetaTrader ou através desse vídeo do YouTube (em português).

Vamos importar as bibliotecas que utilizaremos hoje:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

No código a seguir, os dados se encontram arquivados localmente no formato csv (o link para download do dataset está no nosso canal do Telegram). A partir da função pd.read_csv somos capazes de ler esse formato em um dataframe.

O ativo escolhido foi ITUB4 e selecionamos 8000 registros anteriores à data de análise, o que nos proporciona uma janela de quase 8 anos de dados.

df = pd.read_csv('../data/H2/ITUB4.csv', index_col='time')[["open", "high", "low", "close"]]
df

	open	high	low	close
time
2013-09-03 10:00:00	11.74	11.83	11.67	11.70
2013-09-03 12:00:00	11.71	11.75	11.59	11.60
2013-09-03 14:00:00	11.61	11.67	11.57	11.61
2013-09-03 16:00:00	11.61	11.65	11.57	11.61
2013-09-04 10:00:00	11.58	11.61	11.47	11.53
...	...	...	...	...
2021-04-09 10:00:00	26.53	26.89	26.50	26.87
2021-04-09 12:00:00	26.87	26.99	26.79	26.89
2021-04-09 14:00:00	26.88	26.89	26.58	26.73
2021-04-09 16:00:00	26.73	26.77	26.60	26.66
2021-04-12 10:00:00	26.80	26.97	26.77	26.90

8000 rows × 4 columns

Vamos renomear as colunas de modo que possamos reaproveitar funções desenvolvidas em artigos anteriores. Faremos isso substituindo DataFrame.columns com os nomes que desejamos (obedecendo à ordem).

df.columns = ["Open", "High", "Low", "Close"]
df.head()

	Open	High	Low	Close
time
2013-09-03 10:00:00	11.74	11.83	11.67	11.70
2013-09-03 12:00:00	11.71	11.75	11.59	11.60
2013-09-03 14:00:00	11.61	11.67	11.57	11.61
2013-09-03 16:00:00	11.61	11.65	11.57	11.61
2013-09-04 10:00:00	11.58	11.61	11.47	11.53

Calculando o Estocástico Lento

O Estocástico Lento será calculado a partir da função criada no primeiro artigo dessa série.

def stochastic(df, k_window=8, mma_window=3):
    
    n_highest_high = df["High"].rolling(k_window).max()
    n_lowest_low = df["Low"].rolling(k_window).min()
    
    df["%K"] = (
        (df["Close"] - n_lowest_low) / 
        (n_highest_high - n_lowest_low)
    ) * 100
    df["%D"] = df['%K'].rolling(mma_window).mean()
    
    df["Slow %K"] = df["%D"]
    df["Slow %D"] = df["Slow %K"].rolling(mma_window).mean()
    
    return df

stochastic(df)

	Open	High	Low	Close	%K	%D	Slow %K	Slow %D
time
2013-09-03 10:00:00	11.74	11.83	11.67	11.70	NaN	NaN	NaN	NaN
2013-09-03 12:00:00	11.71	11.75	11.59	11.60	NaN	NaN	NaN	NaN
2013-09-03 14:00:00	11.61	11.67	11.57	11.61	NaN	NaN	NaN	NaN
2013-09-03 16:00:00	11.61	11.65	11.57	11.61	NaN	NaN	NaN	NaN
2013-09-04 10:00:00	11.58	11.61	11.47	11.53	NaN	NaN	NaN	NaN
...	...	...	...	...	...	...	...	...
2021-04-09 10:00:00	26.53	26.89	26.50	26.87	58.730159	26.243386	26.243386	19.867261
2021-04-09 12:00:00	26.87	26.99	26.79	26.89	61.904762	42.592593	42.592593	28.024691
2021-04-09 14:00:00	26.88	26.89	26.58	26.73	38.333333	52.989418	52.989418	40.608466
2021-04-09 16:00:00	26.73	26.77	26.60	26.66	26.666667	42.301587	42.301587	45.961199
2021-04-12 10:00:00	26.80	26.97	26.77	26.90	81.632653	48.877551	48.877551	48.056185

8000 rows × 8 columns

Utilizaremos a função drop para excluir as colunas que não precisaremos para o backtest. Além disso, vamos remover também as linhas que possuem valores NaN através da função dropna.

df.drop(columns=["%K", "%D", "Slow %D"], inplace=True)
df.dropna(inplace=True)
df

	Open	High	Low	Close	Slow %K
time
2013-09-05 12:00:00	11.63	11.79	11.63	11.79	64.153439
2013-09-05 14:00:00	11.79	11.81	11.64	11.74	77.661064
2013-09-05 16:00:00	11.74	11.77	11.71	11.76	88.235294
2013-09-06 10:00:00	11.89	12.03	11.87	11.95	82.901961
2013-09-06 12:00:00	11.95	11.98	11.91	11.95	84.209150
...	...	...	...	...	...
2021-04-09 10:00:00	26.53	26.89	26.50	26.87	26.243386
2021-04-09 12:00:00	26.87	26.99	26.79	26.89	42.592593
2021-04-09 14:00:00	26.88	26.89	26.58	26.73	52.989418
2021-04-09 16:00:00	26.73	26.77	26.60	26.66	42.301587
2021-04-12 10:00:00	26.80	26.97	26.77	26.90	48.877551

7991 rows × 5 columns

Estabelecendo o ponto de entrada

Como dito anteriormente, para efetuar a compra da estratégia nós devemos olhar para uma sequência de 3 candles:

O candle inicial, que deverá apresentar Estocástico Lento menor ou igual a 30, 25 ou 20;
O candle sinal, que deverá ter uma variação positiva (fechamento maior que a abertura);
O candle de entrada, que deverá romper a máxima do candle sinal;

Faremos isso através de uma função strategy_entry, que receberá somente dois argumentos: o df, que deverá conter as colunas "Close", "Open", "High" e "Slow %K" e k_parameter, o valor de $\%K$ que determina o estado de sobrevenda.

Definindo as condições de compra

Considerando que todas as condições acima são respeitadas, o ponto de entrada será a abertura do terceiro candle, caso abra acima da máxima do candle sinal, ou 1 tick acima da máxima caso isso não aconteça.

def strategy_entry(df, k_parameter):

    # Isolate %K from 2 periods behind
    df["Initial Bar"] = df["Slow %K"].shift(2)
    condition_1 = df["Initial Bar"] <= k_parameter

    # Define if the previous candle was positive
    df["Signal Bar"] = np.where(
        df["Close"].shift(1) > df["Open"].shift(1), 
        True, 
        False
    )
    condition_2 = df["Signal Bar"] == True
    
    # Isolate previous High
    df["Previous High"] = df["High"].shift(1)
    condition_3 = df["High"] > df["Previous High"]
    
    # Exponential moving average calculation and variation
    mme80 = df["Close"].ewm(span=80, min_periods=80).mean() 
    mme80_variation = mme80.diff()
    df["MME80 Up"] = np.where(mme80_variation > 0, True, False)
    condition_4 = df["MME80 Up"] == True

    # Buy at market open if above previous high, otherwise 
    # entry one cent above previous high
    df["Buy Price"] = np.where(
        condition_1 & condition_2 & condition_3 & condition_4,
        np.where(
            df["Open"] > df["Previous High"], 
            df["Open"], 
            df["Previous High"] + 0.01
        ),
        np.nan
    )

    return df

No código acima, definimos as seguintes condições:

condition_1: estabelece que o valor do Estocástico de dois candles anteriores (Initial Bar) seja menor ou igual ao valor de k_parameter;
condition_2: define que o candle anterior deva ser um candle positivo (Signal Bar). A coluna Signal Bar será criada através da função np.where, e será True caso o fechamento seja maior que a abertura, e False caso contrário;
condition_3: estabelece que a máxima do candle anterior foi rompida, isto é, a máxima atual deverá ser maior do que a máxima anterior;
condition_4: define que a MME80 deva estar apontada para cima (MME80 Up tem que ser True). A média móvel exponencial é calculada através da função ewm e sua variação, através de diff.

Criando o algoritmo para simular as operações

Com o preço de compra definido, podemos estabelecer as regras de operação do nosso algoritmo. A lógica do código a seguir baseia-se no primeiro algoritmo que criamos para a Estratégia de Máximas e Mínimas e que costumamos utilizar em nossos backtests.

A regra geral é que apenas uma operação pode estar em andamento por vez e esse controle será feito através da variável ongoing. Quando essa variável for Falsa poderemos iniciar uma operação: o algoritmo irá procurar por um valor numérico (~np.nan) na coluna Buy Price. Assim que encontrar, estabeleceremos alguns pontos importantes da estratégia:

entry: a entrada, que será igual ao valor de Buy Price;
stop: o stop loss, que será estabelecido 1 centavo abaixo da mínima (Low) do candle sinal (candle imediatamente anterior ao de entrada);
target: o alvo, que será proporcional ao risco da operação (diferença entre entry e stop). Vamos parametrizar a função com target_factor (que será igual a 2 na nossa simulação);
shares: a quantidade de ações que iremos comprar, que será definida de acordo com o prejuízo (capital_exposure) que estamos dispostos a arriscar por operação. Os lotes deverão ser múltiplos de 100.

Uma vez efetuada a compra, podemos estabelecer as regras de venda (exit):

Venda na abertura: venderemos na abertura se encontrarmos um candle que abra acima do alvo ou abaixo do stop;
Venda no stop: seremos estopados caso a mínima de algum candle rompa a mínima do candle de sinal, ou seja, se encontrarmos uma mínima menor ou igual ao nosso stop;
Venda no alvo: venderemos no alvo se encontrarmos uma máxima maior ou igual ao nosso alvo.

Por fim, o código fará parte da função stochastic_algorithm, que além de receber os argumentos target_factor e capital_exposure mencionados acima, receberá também o dataframe (df) que se deseja rodar o backtest e o capital fixo (initial_capital) disponível para cada operação.

import math

# Create a function to round any number to the smalles multiple of 100
def round_down(x):
    return int(math.floor(x / 100.0)) * 100

def stochastic_algorithm(
    df,
    capital_exposure,
    target_factor,
    initial_capital):

    # List with the total capital after every operation
    total_capital = [initial_capital]

    # List with profits for every operation
    all_profits = [] 

    ongoing = False

    for i in range(0,len(df)):

        if ongoing == True:

            if df["Open"][i] >= target | df["Open"][i] <= stop: 
                exit = df["Open"][i]

                profit = shares * (exit - entry)

                # Append profit to list and create a new entry with the capital
                # after the operation is complete
                all_profits += [profit]
                current_capital = total_capital[-1] # current capital is the last entry in the list
                total_capital += [current_capital + profit]

                ongoing = False

            elif df["Low"][i] <= stop: 
                exit = stop

                profit = shares * (exit - entry)

                # Append profit to list and create a new entry with the capital
                # after the operation is complete
                all_profits += [profit]
                current_capital = total_capital[-1] # current capital is the last entry in the list
                total_capital += [current_capital + profit]

                ongoing = False

            elif df["High"][i] >= target: 
                exit = target

                profit = shares * (exit - entry)
                # Append profit to list and create a new entry with the capital
                # after the operation is complete

                all_profits += [profit]
                current_capital = total_capital[-1] # current capital is the last entry in the list
                total_capital += [current_capital + profit]

                ongoing = False

        else:
            if ~(np.isnan(df["Buy Price"][i])):

                entry = df["Buy Price"][i]
                stop = df["Low"][i-1] - 0.01
                risk = entry - stop
                target = entry + (risk * target_factor)
                shares = round_down(capital_exposure / risk)

                ongoing = True

    return all_profits, total_capital

Calculando a estatística e a curva de capital

As funções a seguir foram criadas em artigos passados e são amplamente utilizadas em nossos backtests.

Através delas obteremos informações relevantes como o número total de operações, número de operações que deram lucro ou prejuízo, lucro total e seu percentual, drawdown e o gráfico da evolução da curva de capital.

def get_drawdown(data, column = "Close"):
    data["Max"] = data[column].cummax()
    data["Delta"] = data['Max'] - data[column]
    data["Drawdown"] = 100 * (data["Delta"] / data["Max"])
    max_drawdown = data["Drawdown"].max()
    return max_drawdown

def strategy_test(all_profits, total_capital):
    gains = sum(x >= 0 for x in all_profits)
    losses = sum(x < 0 for x in all_profits)
    num_operations = gains + losses
    pct_gains = 100 * (gains / num_operations)
    pct_losses = 100 - pct_gains
    total_profit = sum(all_profits)
    pct_profit = (total_profit / total_capital[0]) * 100
    
    # Compute drawdown
    total_capital = pd.DataFrame(data=total_capital, columns=["total_capital"])
    drawdown = get_drawdown(data=total_capital, column="total_capital")

    return {
        "num_operations": num_operations,
        "gains": gains ,
        "pct_gains": pct_gains.round(),
        "losses": losses,
        "pct_losses": pct_losses.round(), 
        "total_profit": total_profit,
        "pct_profit": pct_profit,
        "drawdown": drawdown
    }

def capital_plot(total_capital, all_profits):
  all_profits = [0] + all_profits # make sure both lists are the same size
  cap_evolution = pd.DataFrame({'Capital': total_capital, 'Profit': all_profits})
  plt.title("Curva de Capital")
  plt.xlabel("Total Operações")
  cap_evolution['Capital'].plot()

Realizando o backtest

O último passo para realização do nosso backtest é rodar as funções anteriores iterando sobre a lista de parâmetros do Estocástico Lento (k_parameters).

As informações obtidas através da função strategy_test serão armazenadas em um dicionário (statistics) para posterior análise dos resultados.

Na simulação, entraremos sempre com um capital fixo de $100,000 e um risco controlado de 1% desse capital ($1,000). Buscaremos um payoff igual a 2x o nosso risco.

k_parameters = [30, 25, 20]

statistics  = {}
for k in k_parameters:
    
    df = strategy_entry(df, k)
    all_profits, total_capital = stochastic_algorithm(
        df, 
        capital_exposure = 1000,
        target_factor = 2,
        initial_capital = 100000
    )
    capital_plot(total_capital, all_profits)
    statistics[k] = strategy_test(all_profits, total_capital)

legend = [f"%K <= {k}" for k in k_parameters]
plt.legend(legend)

<matplotlib.legend.Legend at 0x7f35dc1e4b10>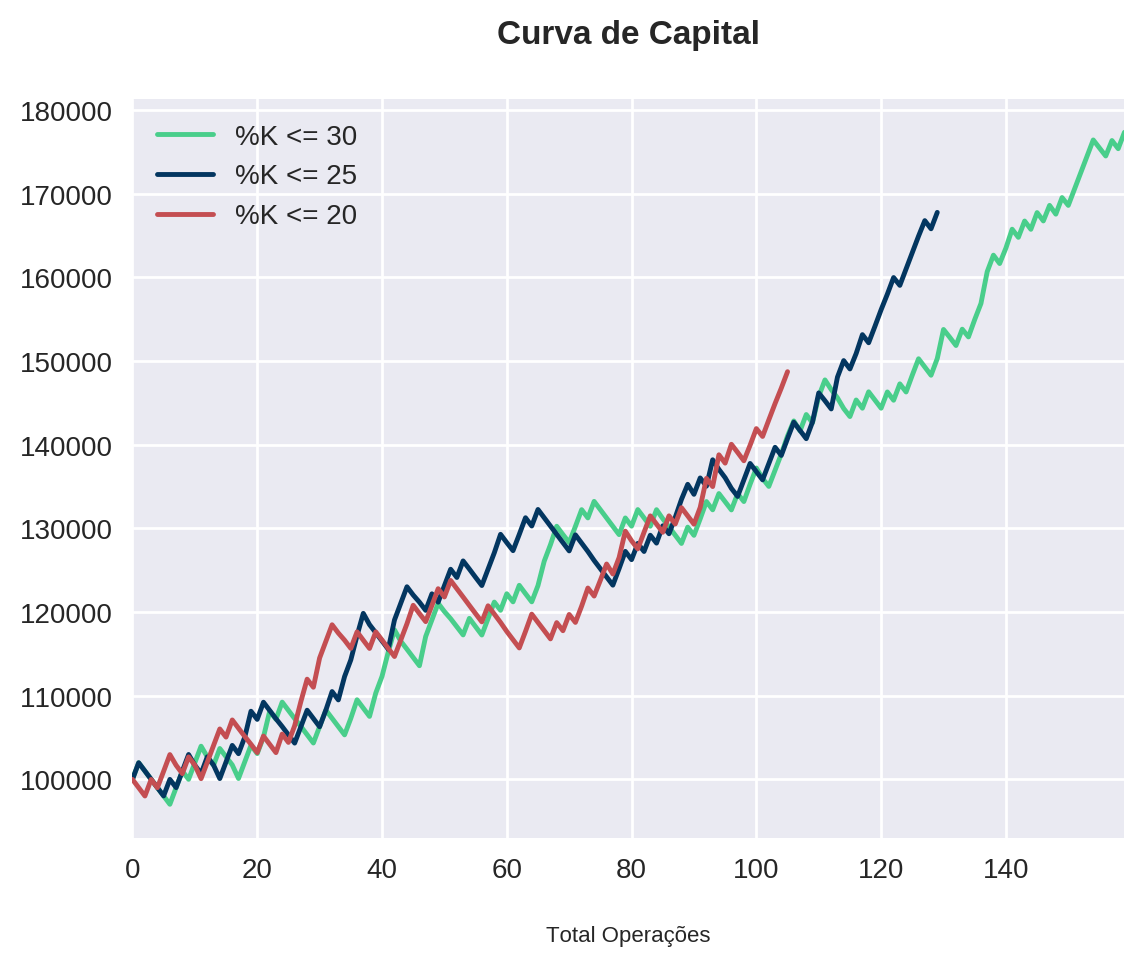

Vamos transformar statistics em um dataframe a fim de obtermos uma melhor visualização dos dados. Faremos isso através da função pd.DataFrame.from_dict e determinaremos que as chaves corresponderão aos índices através do argumento orient.

statistics = pd.DataFrame.from_dict(statistics, orient='index')
statistics

	num_operations	gains	pct_gains	losses	pct_losses	total_profit	pct_profit	drawdown
30	159	76	48.0	83	52.0	77334.0	77.334	4.869009
25	129	63	49.0	66	51.0	67762.0	67.762	6.840366
20	105	49	47.0	56	53.0	48724.0	48.724	6.517313

Podemos observar que quanto maior o $\%K$ , maior o número de operações (o que é natural uma vez que estamos sendo menos seletivos). Além disso, todas apresentaram uma taxa semelhante de acertos.

Para uma análise mais fiel dos resultados, vamos calcular o lucro percentual por operação.

Calculando o lucro por operação

A função a seguir foi criada em um dos artigos de backtest da estratégia de IFR2. Seu funcionamento é bem simples: ela divide o lucro percentual pelo número de operações.

def profit_per_operation(data, strategy_title):
    profit = data["pct_profit"] / data["num_operations"]
    df = pd.DataFrame(profit).round(2)
    df.rename(columns = {0: "profit_per_operation"}, inplace=True)
    print(strategy_title, "\n\n", df)

profit_per_operation(
  statistics, 
  strategy_title="Estratégia de Estocástico Lento:"
)

Estratégia de Estocástico Lento: 

     profit_per_operation
30                  0.49
25                  0.53
20                  0.46

Valor Esperado (Expected Value)

Uma vez que estamos limitando nosso risco (em $1,000) e nosso lucro (2x o risco), podemos calcular o valor esperado (ou expectativa matemática) da estratégia. No nosso caso:

$EV = P_{gain} \times payoff + P_{loss} \times risk$

Onde $P_{gain}$ é a probabilidade de acerto (pct_gains) e $P_{loss}$ é a probabilidade de erro (pct_losses). Ora, como nossa taxa de acerto ficou em 50% e o payoff é 2x o risco, temos que:

$EV = 0.5 \times (2 \times 1000) + 0.5 \times (-1000)$
$EV = 1000 - 500 = 500$

Isso significa que para um capital de $100,000, o lucro percentual por operação esperado é igual a $0.5\%$ , o que está em linha com o valor encontrado.

Conclusão

De uma maneira geral, todas as estratégias obtiveram resultados satisfatórios.

A estratégia que apresentou o melhor resultado financeiro e menor drawdown foi com $\%K$ abaixo de 30. Ainda assim, o lucro percentual por operação ficou um pouco abaixo da estratégia com $\%K$ menor que 25.

Note que temos a impressão que $\%K$ abaixo de 25 performou significativamente melhor que $\%K$ abaixo de 20, devido a diferença de aproximadamente 20% (em números absolutos) do lucro percentual. Porém, quando olhamos para o lucro percentual por operação, vemos que há pouca diferença entre elas. Além disso, ambas estratégias apresentaram valores de drawdown máximo na faixa dos 6%, o que configura um bom limiar de risco.

Essa análise levou em consideração apenas um sistema operacional que podemos utilizar com o Estocástico Lento. Nos próximos artigos iremos testar diferentes combinações de parâmetros, como timeframes, períodos de $\%K$ e pontos de entrada e saída, a fim de buscar a estratégia mais lucrativa.

Se esse assunto te interessa, não deixe de se inscrever na nossa newsletter e fazer parte do nosso grupo no Telegram! Lá você fica sabendo em primeira mão quando lançamos novos posts, além de interagir com o nosso bot para receber informações sobre o IFR, Estocástico e até de backtests dos seus ativos favoritos.