Como Calcular o Estocástico Lento Utilizando Python

Criado na década de 50 pelo americano George Lane, o indicador Estocástico faz parte da família dos osciladores de momento, muito utilizados como sinalizadores de reversão de tendência na análise técnica.

Na prática, o Estocástico mede a relação entre o preço atual com as máximas e mínimas de um período pré-determinado. Originalmente, utilizava-se 14 períodos, mas atualmente tornou-se comum sua utilização em intervalos mais curtos, como em uma janela de 8 períodos.

Dito isso, nós definimos o conceito de Estocástico Rápido $(\%K)$ , usualmente acompanhado de sua média móvel aritmética de n períodos $(\%D)$ .

Essas curvas são calculadas da seguinte maneira:

$\%K = \left(\dfrac{PA - Min(n)}{Max(n) - Min(n)} \right) *100$

$\%D = MMA(\%K, n)$

PA = Preço Atual;
Min(n) = Mínima em n períodos;
Max(n) = Máxima em n períodos;
MMA = Média Móvel Aritmética.

Estocástico Lento

Para calcular o Estocástico Lento, tudo que precisamos fazer é calcular a média móvel aritmética das curvas acima. Ou seja, $\%K_L = \%D$ . Matematicamente:

$\%K_L = MMA(\%K, 3) = \%D$

$\%D_L = MMA(\%D)$

Dessa forma, o Estocástico Lento suaviza as oscilações de preço e, por conta disso, é bastante utilizado entre traders.

Além disso, análogo ao IFR, esse indicador também varia em uma escala de 0 a 100, apresentando regiões que caracterizam estados de sobrecompra e sobrevenda (tipicamente acima de 80 e abaixo de 20).

Agora que nós já vimos o conceito de Estocástico e suas variações, vamos criar uma função, em Python, para calculá-lo em apenas 3 passos:

1. Calcular o Estocástico Rápido;
2. Calcular o Estocástico Lento;
3. Criar a função juntando os passos acima.

Simples assim, vamos trabalhar!

Calculando o Estocástico Rápido

Calcularemos as curvas $\%K$ e $\%D$ , que caracterizam o estocástico rápido, a partir das fórmulas descritas anteriormente. Mas para isso, precisamos importar as bibliotecas de interesse e baixar os dados necessários.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import yfinance as yf

Faremos o download das colunas com o preço de fechamento ajustado, máximas e mínimas de um ativo qualquer (VVAR3), dentro de um período de 1 ano (01/01/2020 - 31/12/2020).

tickers = "VVAR3.SA"
start = "2020-01-01"
end = "2020-12-31"

df = yf.download(tickers, start= start, end=end).copy()[["High", "Low", "Adj Close"]]
df

[*********************100%***********************]  1 of 1 completed

	High	Low	Adj Close
Date
2020-01-02	11.760000	11.23	11.730000
2020-01-03	12.000000	11.47	11.480000
2020-01-06	11.680000	11.20	11.480000
2020-01-07	11.650000	11.42	11.650000
2020-01-08	11.830000	11.45	11.600000
...	...	...	...
2020-12-22	16.450001	15.86	15.940000
2020-12-23	16.580000	15.71	16.129999
2020-12-28	16.700001	16.00	16.590000
2020-12-29	16.840000	16.48	16.580000
2020-12-30	16.780001	16.16	16.160000

247 rows × 3 columns

Para o cálculo da curva $\%K$ , precisamos primeiro isolar as máximas e mínimas do período escolhido. Isto é, a cada linha isolaremos o valor máximo da coluna High e o mínimo da coluna Low dentre as $n$ linhas anteriores.

Utilizaremos a função rolling que faz essa seleção de uma janela móvel, especificada pelo argumento $n$ , associada às funções max e min. A janela escolhida foi de 8 períodos.

n = 8 
n_highest_high = df["High"].rolling(n).max()
n_lowest_low = df["Low"].rolling(n).min()

Agora basta inseri-los na fórmula do Estocástico e teremos os valores para curva $\%K$ do estocástico rápido.

df["%K"] = (
    (df["Adj Close"] - n_lowest_low) / 
    (n_highest_high - n_lowest_low)
) * 100

df

	High	Low	Adj Close	%K
Date
2020-01-02	11.760000	11.23	11.730000	NaN
2020-01-03	12.000000	11.47	11.480000	NaN
2020-01-06	11.680000	11.20	11.480000	NaN
2020-01-07	11.650000	11.42	11.650000	NaN
2020-01-08	11.830000	11.45	11.600000	NaN
...	...	...	...	...
2020-12-22	16.450001	15.86	15.940000	46.590886
2020-12-23	16.580000	15.71	16.129999	53.787839
2020-12-28	16.700001	16.00	16.590000	71.212116
2020-12-29	16.840000	16.48	16.580000	73.622044
2020-12-30	16.780001	16.16	16.160000	57.086608

247 rows × 4 columns

Com os valores de $\%K$ definidos, podemos calcular a média móvel aritmética para obtermos $\%D$ . A função utilizada para isso é a mesma (rolling), dessa vez associada à função mean.

Feito isso, removeremos todas as linhas contendo NaN.

df["%D"] = df['%K'].rolling(3).mean()
df.dropna(inplace=True)
df.head()

	High	Low	Adj Close	%K	%D
Date
2020-01-15	13.56	13.10	13.55	99.576262	99.704444
2020-01-16	14.03	13.38	13.59	83.141776	94.085036
2020-01-17	13.87	13.21	13.73	88.372085	90.363374
2020-01-20	14.25	13.65	14.01	91.011245	87.508369
2020-01-21	14.37	13.78	14.32	98.188399	92.523910

Calculando o Estocástico Lento

O Estocástico Lento é ainda mais simples de se calcular, uma vez que ele é oriundo das curvas do estocástico rápido.

Como visto anteriormente, a curva %K lento ( $\%K_L$ ) nada mais é do que a curva suavizada através da média móvel de %K rápido ( $\%K$ ). Em outras palavras, $\%K_L$ é igual a %D rápido ( $\%D$ ).

A curva %D lento ( $\%D_L$ ), por sua vez, nada mais é do que a média móvel aritmética de $\%K_L$ .

df["Slow %K"] = df["%D"]
df["Slow %D"] = df["Slow %K"].rolling(3).mean()
df.head()

	High	Low	Adj Close	%K	%D	Slow %K	Slow %D
Date
2020-01-15	13.56	13.10	13.55	99.576262	99.704444	99.704444	NaN
2020-01-16	14.03	13.38	13.59	83.141776	94.085036	94.085036	NaN
2020-01-17	13.87	13.21	13.73	88.372085	90.363374	90.363374	94.717618
2020-01-20	14.25	13.65	14.01	91.011245	87.508369	87.508369	90.652260
2020-01-21	14.37	13.78	14.32	98.188399	92.523910	92.523910	90.131884

Para ilustrar, vamos plotar ambas as curvas em um gráfico de linha. É muito simples, basta utilizar a função plot.

Para complementar, nós podemos plotar linhas horizontais através da função axhline para delimitar as regiões de sobrecompra e sobrevenda

df[["Slow %K", "Slow %D"]].plot()
plt.axhline(y=20.0, color='black', linestyle='--', linewidth=1)
plt.axhline(y=80.0, color='black', linestyle='--', linewidth=1)
plt.ylim(0, 100.0)

(0, 100.0)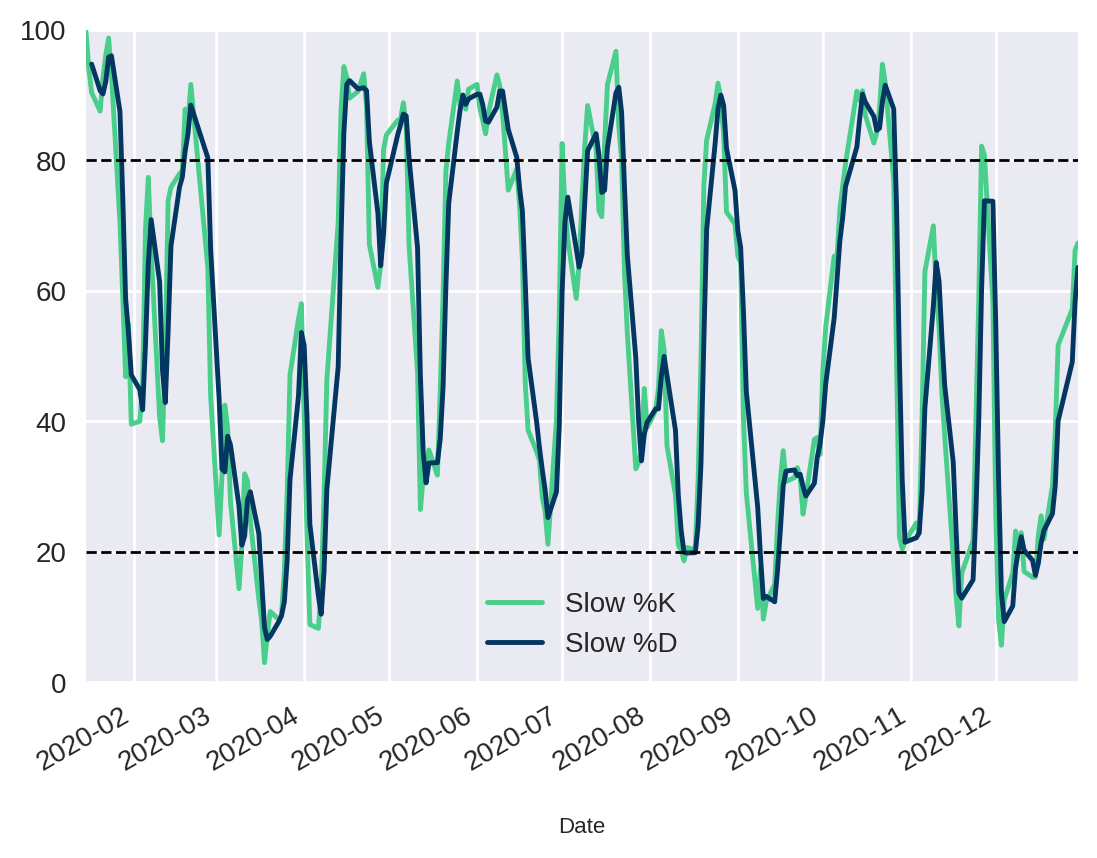

Assim como fizemos no artigo do IFR, nós podemos plotar o estocástico juntamente com o gráfico do preço de fechamento.

Faremos isso através da função plot_stochastic, que recebe como argumento apenas o dataframe que contém as colunas necessárias (Adj Close, Slow %K e Slow %D).

def plot_stochastic(df):
    fig, (ax1, ax2) = plt.subplots(
        nrows=2, 
        sharex=True,
        figsize=(12,8), 
        gridspec_kw={"height_ratios": [3, 1]})

    ax1.plot(df.index, df["Adj Close"], label="Fechamento")
    ax1.legend()

    ax2.plot(df.index, df[["Slow %K"]], label='Estocástico Lento')
    ax2.plot(df.index, df[["Slow %D"]], label='MMA(3)', linewidth=1)
    ax2.axhline(y=80, color='black', linestyle='--', linewidth=1)
    ax2.axhline(y=20, color='black', linestyle='--', linewidth=1)
    ax2.set_ylim(0, 100)
    ax2.legend()

plot_stochastic(df)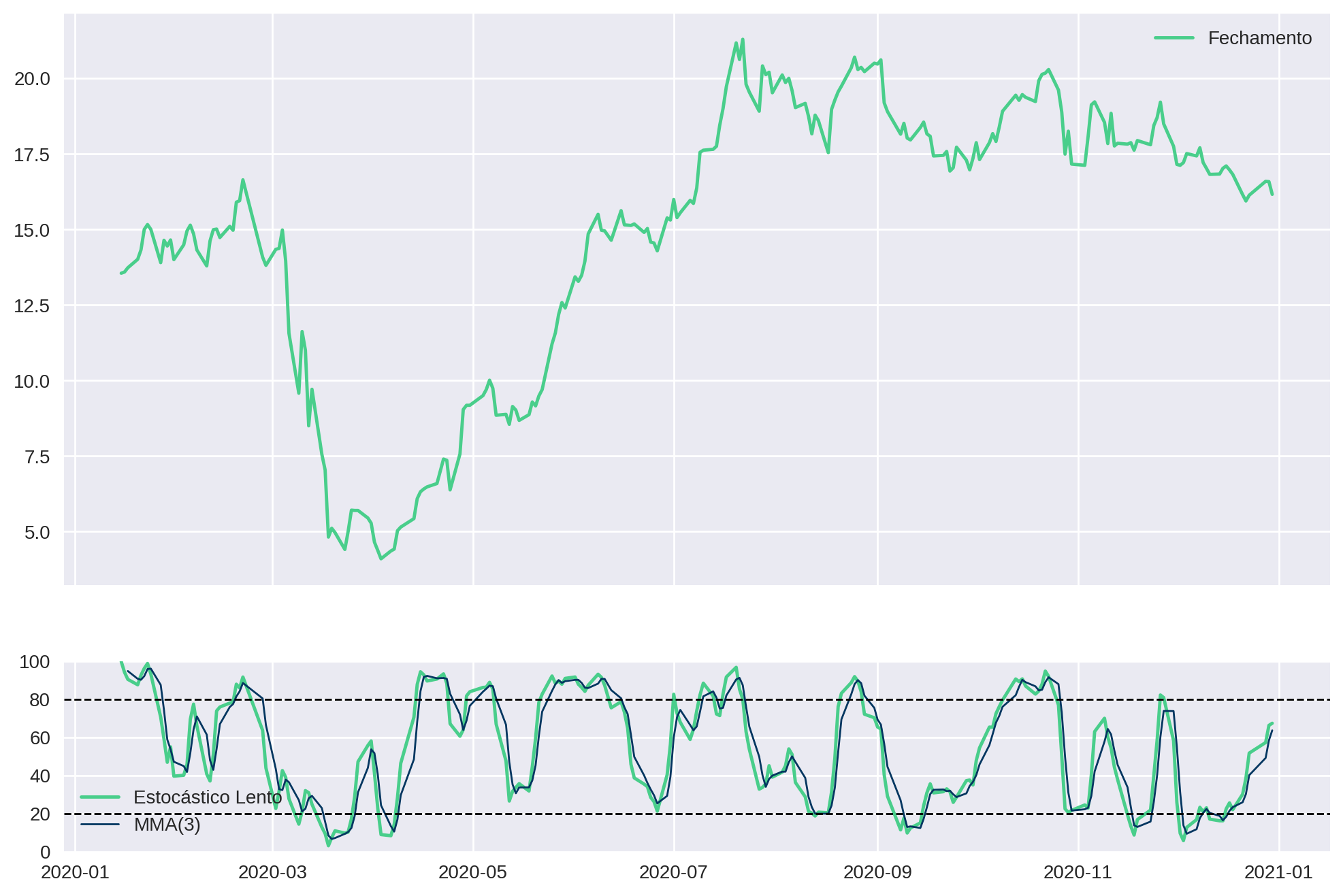

Criando uma função para o cálculo do Estocástico

Finalmente, podemos juntar tudo que fizemos até agora em uma função stochastic, que retornará o dataframe selecionado com as colunas %K, %D, Slow %K e Slow %D.

Essa função receberá 3 argumentos:

df: o dataframe que se deseja adicionar as colunas acima (lembrando que ele deve conter as colunas High, Low e Adj Close);
k_window: janela móvel que se deseja calcular o estocástico (será de 8 períodos, por padrão);
mma_window: janela móvel que se deseja calcular média móvel aritmética (será de 3 períodos, por padrão).

def stochastic(df, k_window=8, mma_window=3):
    
    n_highest_high = df["High"].rolling(k_window).max()
    n_lowest_low = df["Low"].rolling(k_window).min()
    
    df["%K"] = (
        (df["Adj Close"] - n_lowest_low) / 
        (n_highest_high - n_lowest_low)
    ) * 100
    df["%D"] = df['%K'].rolling(mma_window).mean()
    
    df["Slow %K"] = df["%D"]
    df["Slow %D"] = df["Slow %K"].rolling(mma_window).mean()
    
    return df

Vamos testar em um ativo qualquer:

ticker = "PETR4.SA"
petr4_df = yf.download(ticker, start=start, end=end).copy()[["High", "Low", "Adj Close"]]
stochastic(petr4_df)

[*********************100%***********************]  1 of 1 completed

	High	Low	Adj Close	%K	%D	Slow %K	Slow %D
Date
2020-01-02	30.700001	30.309999	30.697725	NaN	NaN	NaN	NaN
2020-01-03	31.240000	30.450001	30.447742	NaN	NaN	NaN	NaN
2020-01-06	30.940001	29.950001	30.807716	NaN	NaN	NaN	NaN
2020-01-07	30.879999	30.469999	30.687725	NaN	NaN	NaN	NaN
2020-01-08	30.770000	30.240000	30.497738	NaN	NaN	NaN	NaN
...	...	...	...	...	...	...	...
2020-12-22	27.469999	27.049999	27.280001	40.641747	50.935638	50.935638	70.116206
2020-12-23	28.250000	27.350000	27.950001	76.470648	47.950126	47.950126	55.698310
2020-12-28	28.520000	28.180000	28.180000	82.999992	66.704129	66.704129	55.196631
2020-12-29	28.430000	27.990000	28.270000	87.500000	82.323547	82.323547	65.659267
2020-12-30	28.490000	28.200001	28.340000	90.999985	87.166659	87.166659	78.731445

247 rows × 7 columns

plot_stochastic(petr4_df)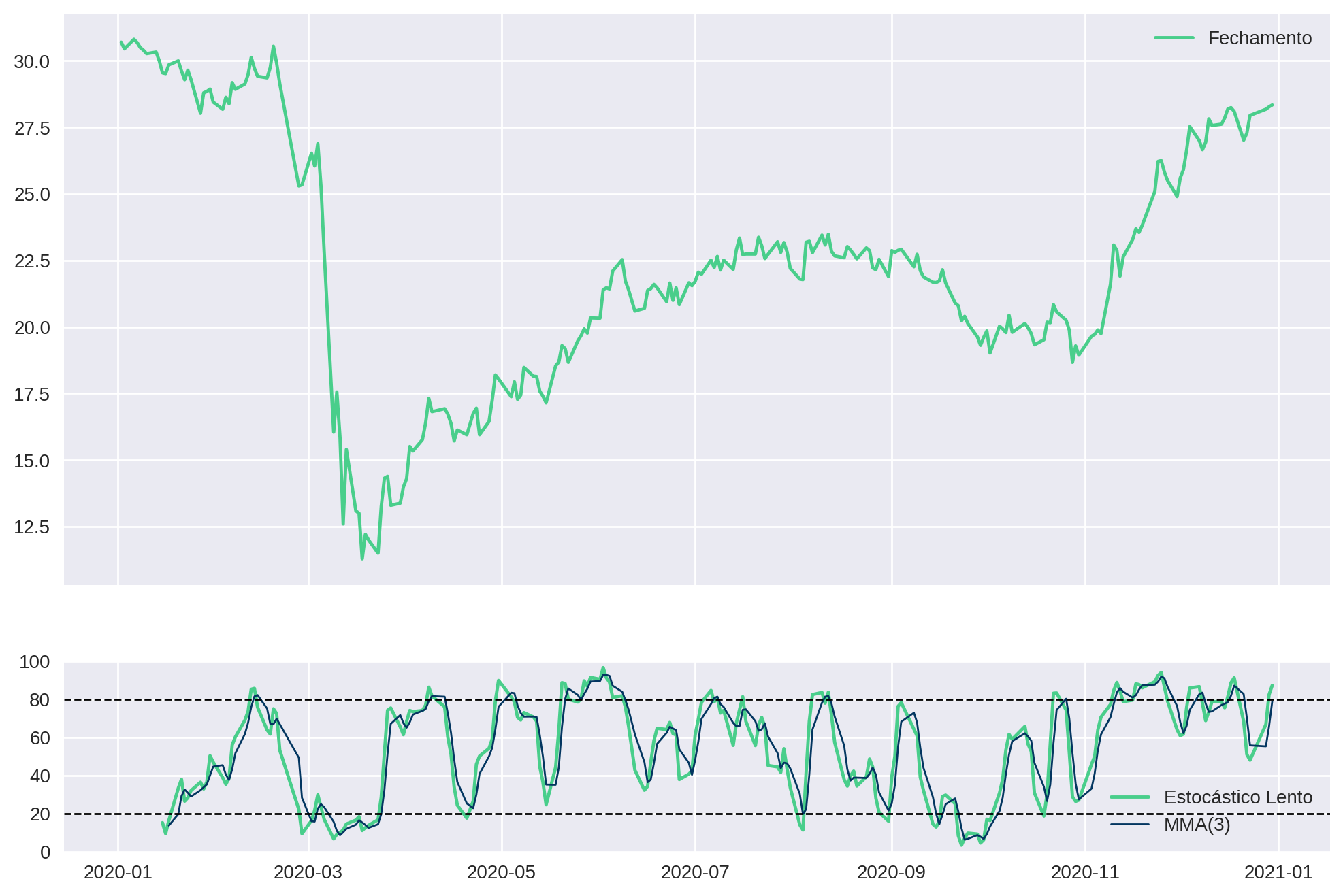

Conclusão

O indicador Estocástico é amplamente utilizado em setups a fim de se beneficiar das oscilações do mercado, embarcando no início de uma perna, seja ela de alta ou de baixa.

A partir de stochastic nós podemos dar início a uma série de backtests utilizando esse indicador. A ideia é testarmos diversas estratégias em vários timeframes.

Dependendo do sistema operacional utilizado, o Estocástico demonstra tanta consistência quanto o IFR2, mas com uma média de sinais ainda maior. Então, se você gostou da série de backtests de IFR2, você não vai querer perder essa! Fique ligado na nossa newsletter ou no Telegram, nós anunciamos tudo por lá.