Entenda o Drawdown e Calcule essa Medida de Volatilidade para Qualquer Ativo
O drawdown é uma importante medida de volatilidade para os investidores. De forma simples, o drawdown é calculado como a porcentagem de quanto um ativo, fundo ou portfólio caiu em relação ao seu topo.
Suponha que o Ibovespa esteja cotado a 100.000 pontos em uma determinada data. Durante os próximos dias, ele cai para 90.000 sem superar a marca dos 100.000 pontos. O drawdown nesse período foi de 10%.
Agora, se depois de alcançar os 90.000 pontos o Ibovespa suba para 115.000 pontos, o próximo drawdown será calculado utilizando o mais novo topo. Nesse caso, se ele cair para 100.000 logo em seguida, o drawdown será de:
A importância do drawdown
O drawdown é bastante utilizado para medir a volatilidade, ou o risco, de um determinado investimento. Se dois ativos, A e B, possuem o mesmo retorno ao longo de um período, mas o drawdown de A é menor que o de B, o ativo A tende a ser preferível.
A discussão entre volatilidade x risco é extensa e está além do escopo desse artigo. No entanto, como exemplos, se um investimento observa quedas maiores, o investidor incorre no risco:
- de ter uma chamada de margem (caso alavancado),
- de encerrar o investimento prematuramente antes da recuperação (comum em fundos de investimento),
- e de precisar resgatar em um momento de forte queda (devido a uma emergência ou até mesmo para a aposentadoria).
No caso específico de uma estratégia de trade, um menor drawdown significa uma menor exposição ao risco, e portanto minimizá-lo pode ser interessante mesmo que a rentabilidade da estratégia caia.
O que é melhor: uma estratégia A com rentabilidade de 20% e um drawdown de 15%, ou uma estratégia B com rentabilidade de 25% e drawdown de 40%? Mesmo que a resposta correta não exista, uma vez que é dependente da gestão de risco e perfil de cada pessoa, calcular o drawdown é de suma importância para qualquer investimento.
Calculando o drawdown do Ibovespa
Nossa primeira tarefa será calcular o drawdown máximo do Ibovespa em um determinado período. É importante entender o termo drawdown máximo: ele é a medida do maior drawdown ocorrido no período estabelecido. No exemplo anterior, a primeira queda foi de 100.000 para 90.000 (drawdown de 10%), e depois de 115.000 para 100.000 (drawdown de 13%). Um investidor analisando esse período específico observaria que o drawdown máximo foi de 13%.
O primeiro passo é importar as bibliotecas que vamos utilizar e baixar os preços de fechamento do Ibovespa em 2020 utilizando o Yahoo Finance. Note que o ticker do Ibovespa no yfinance é ^BVSP. Os símbolos podem ser pesquisados diretamente na plataforma.
# %%capture means we suppress the output
%%capture
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
!pip install yfinance
import yfinance as yfdata = yf.download("^BVSP", start="2020-01-01", end="2020-12-31").copy()[['Adj Close']]
data.head() # returns the first 5 rows of the dataframe| Adj Close | |
|---|---|
| Date | |
| 2020-01-02 | 118573.0 |
| 2020-01-03 | 117707.0 |
| 2020-01-06 | 116878.0 |
| 2020-01-07 | 116662.0 |
| 2020-01-08 | 116247.0 |
Em seguida vamos utilizar a função cummax para criar uma nova coluna com o valor máximo de Adj Close até o elemento em questão. Repare a diferença entre cummax e max: enquanto cummax retorna, para cada elemento, o valor máximo anterior ou igual a ele, max retorna o valor máximo na coluna inteira, independente de ter ocorrido antes ou depois do elemento.
data["Max"] = data['Adj Close'].cummax()
data.head(20)| Adj Close | Max | |
|---|---|---|
| Date | ||
| 2020-01-02 | 118573.0 | 118573.0 |
| 2020-01-03 | 117707.0 | 118573.0 |
| 2020-01-06 | 116878.0 | 118573.0 |
| 2020-01-07 | 116662.0 | 118573.0 |
| 2020-01-08 | 116247.0 | 118573.0 |
| 2020-01-09 | 115947.0 | 118573.0 |
| 2020-01-10 | 115503.0 | 118573.0 |
| 2020-01-13 | 117325.0 | 118573.0 |
| 2020-01-14 | 117632.0 | 118573.0 |
| 2020-01-15 | 116414.0 | 118573.0 |
| 2020-01-16 | 116704.0 | 118573.0 |
| 2020-01-17 | 118478.0 | 118573.0 |
| 2020-01-20 | 118862.0 | 118862.0 |
| 2020-01-21 | 117026.0 | 118862.0 |
| 2020-01-22 | 118391.0 | 118862.0 |
| 2020-01-23 | 119528.0 | 119528.0 |
| 2020-01-24 | 118376.0 | 119528.0 |
| 2020-01-27 | 114482.0 | 119528.0 |
| 2020-01-28 | 116479.0 | 119528.0 |
| 2020-01-29 | 115385.0 | 119528.0 |
Agora que temos o valor do último topo (Max) para cada linha, podemos calcular o drawdown (em %):
data["Delta"] = data["Max"] - data["Adj Close"]
data["Drawdown"] = 100 * (data["Delta"] / data["Max"])
data.head(20)| Adj Close | Max | Delta | Drawdown | |
|---|---|---|---|---|
| Date | ||||
| 2020-01-02 | 118573.0 | 118573.0 | 0.0 | 0.000000 |
| 2020-01-03 | 117707.0 | 118573.0 | 866.0 | 0.730352 |
| 2020-01-06 | 116878.0 | 118573.0 | 1695.0 | 1.429499 |
| 2020-01-07 | 116662.0 | 118573.0 | 1911.0 | 1.611665 |
| 2020-01-08 | 116247.0 | 118573.0 | 2326.0 | 1.961661 |
| 2020-01-09 | 115947.0 | 118573.0 | 2626.0 | 2.214669 |
| 2020-01-10 | 115503.0 | 118573.0 | 3070.0 | 2.589122 |
| 2020-01-13 | 117325.0 | 118573.0 | 1248.0 | 1.052516 |
| 2020-01-14 | 117632.0 | 118573.0 | 941.0 | 0.793604 |
| 2020-01-15 | 116414.0 | 118573.0 | 2159.0 | 1.820819 |
| 2020-01-16 | 116704.0 | 118573.0 | 1869.0 | 1.576244 |
| 2020-01-17 | 118478.0 | 118573.0 | 95.0 | 0.080119 |
| 2020-01-20 | 118862.0 | 118862.0 | 0.0 | 0.000000 |
| 2020-01-21 | 117026.0 | 118862.0 | 1836.0 | 1.544648 |
| 2020-01-22 | 118391.0 | 118862.0 | 471.0 | 0.396258 |
| 2020-01-23 | 119528.0 | 119528.0 | 0.0 | 0.000000 |
| 2020-01-24 | 118376.0 | 119528.0 | 1152.0 | 0.963791 |
| 2020-01-27 | 114482.0 | 119528.0 | 5046.0 | 4.221605 |
| 2020-01-28 | 116479.0 | 119528.0 | 3049.0 | 2.550867 |
| 2020-01-29 | 115385.0 | 119528.0 | 4143.0 | 3.466133 |
Pronto! O código acima nos diz qual o drawdown atual do ativo, dentro do período selecionado, em qualquer momento do tempo. Assim, podemos rapidamente dizer que o drawdown do Ibovespa em 2020, no dia 27 de Janeiro de 2020, era de 4,22%.
Como fazemos então para calcular o drawdown máximo no período?
max_drawdown = data["Drawdown"].max()
max_drawdown
46.815808848136
Simples assim. O drawdown máximo do Ibovespa em 2020 foi de impressionantes 46,18% (2020 não foi pra amadores!)
Encontrando o período de máximo drawdown no gráfico
Como sempre, faz parte das nossas análises facilitar o entendimento com a melhor visualização possível. Vamos então identificar, via código, os pontos que compreenderam o drawdown máximo de 2020 e marcá-los em um gráfico.
# Get the position of the point with maximum Drawdown value
bottom_day = np.argmax(data['Drawdown'])
bottom_index = data[['Drawdown']].index.get_loc(bottom_day)
print(bottom_day, bottom_index, sep="\n")2020-03-23 00:00:00 54
Repare que nós utilizamos argmax para retornar o índice (no caso, o dia) onde observamos o maior drawdown. Esse dia é o fundo do mercado e foi observado na linha 55 (índice número 54).
Para identificar o topo, vamos achar o valor máximo do Ibovespa na data do fundo, e buscar quando foi a primeira ocorrência desse preço.
# Get the position of the point with peak value before bottom
max_value = data.iloc[bottom_index]['Max']
top_day = (data['Max'] == max_value).idxmax()
top_index = data[['Max']].index.get_loc(top_day)
print(top_day, top_index, sep="\n")2020-01-23 00:00:00 15
Dessa vez usamos idxmax para retornar a primeira ocorrência de quando o index foi igual ao valor máximo observado anteriormente ao fundo estabelecido. O topo foi definido no dia 23 de Janeiro de 2020, no 16º pregão do ano.
Plotando os pontos de topo e fundo
Com os pontos em mãos, podemos utilizar o matplotlib para visualizar esse período no gráfico:
data["Adj Close"].plot(
marker='o',
markerfacecolor="red",
markevery=[top_index, bottom_index],
)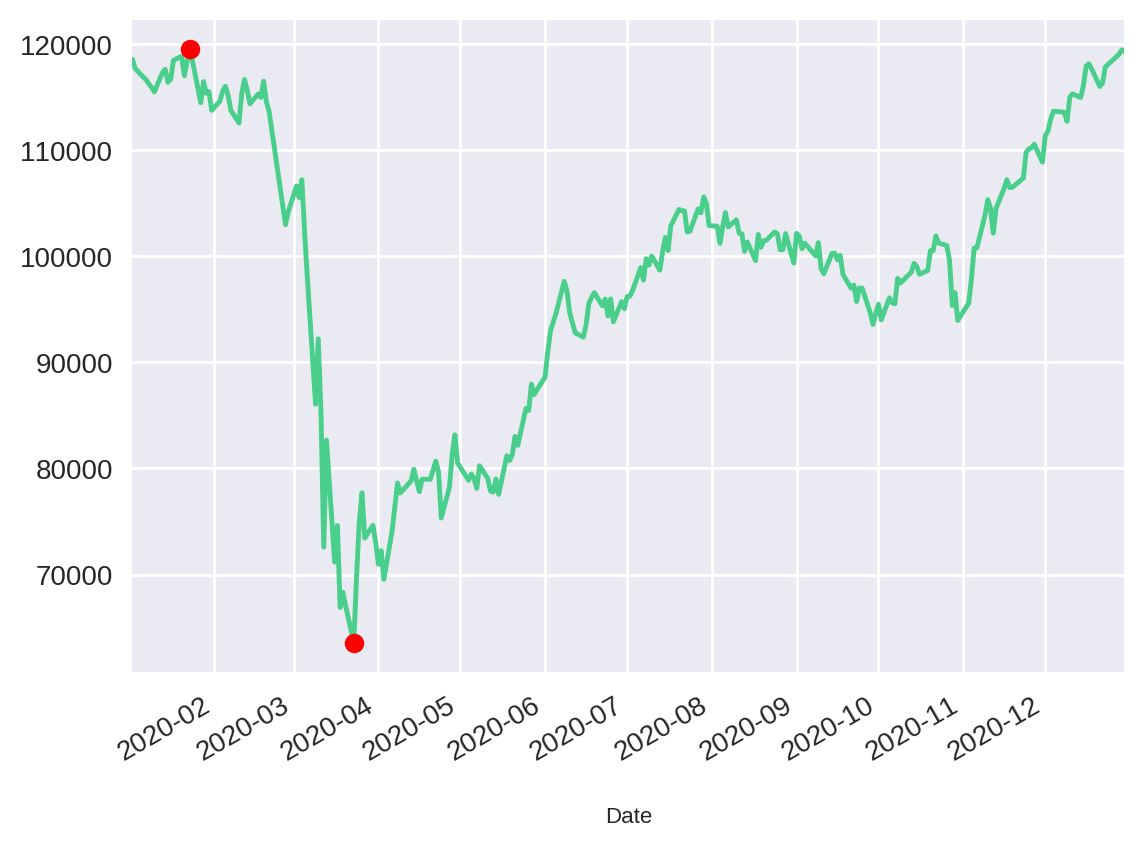
Veja como a visualização nos ajuda a confirmar que os pontos marcados em vermelho foram, de fato, os pontos que compreenderam a maior queda do Ibovespa durante o ano de 2020.
Calculando o drawdown de vários anos
Nosso código está pronto e é capaz de nos retornar o drawdown em qualquer período, para qualquer ativo. Vamos facilitar ainda mais a nossa vida e escrever um código que nos permita analisar o drawdown máximo por ano em um determinado período.
O primeiro passo é transformar o cálculo do drawdown máximo em uma função:
def get_drawdown(data, column = "Adj Close"):
data["Max"] = data[column].cummax()
data["Delta"] = data['Max'] - data[column]
data["Drawdown"] = 100 * (data["Delta"] / data["Max"])
max_drawdown = data["Drawdown"].max()
return max_drawdownAgora, vamos baixar as cotações do Ibovespa dos últimos 5 anos:
start_date = "2015-01-01"
end_date = "2020-12-31"
data = yf.download("^BVSP", start=start_date, end=end_date).copy()[['Adj Close']]
data| Adj Close | |
|---|---|
| Date | |
| 2015-01-02 | 48512.0 |
| 2015-01-05 | 47517.0 |
| 2015-01-06 | 48001.0 |
| 2015-01-07 | 49463.0 |
| 2015-01-08 | 49943.0 |
| ... | ... |
| 2020-12-22 | 116348.0 |
| 2020-12-23 | 117857.0 |
| 2020-12-28 | 119051.0 |
| 2020-12-29 | 119475.0 |
| 2020-12-30 | 119306.0 |
1480 rows × 1 columns
Nós podemos facilmente filtrar os dados por ano:
data_in_2019 = data[data.index.year == 2019]
data_in_2019
| Adj Close | |
|---|---|
| Date | |
| 2019-01-02 | 91012.0 |
| 2019-01-03 | 91564.0 |
| 2019-01-04 | 91841.0 |
| 2019-01-07 | 91699.0 |
| 2019-01-08 | 92032.0 |
| ... | ... |
| 2019-12-20 | 115121.0 |
| 2019-12-23 | 115863.0 |
| 2019-12-26 | 117203.0 |
| 2019-12-27 | 116534.0 |
| 2019-12-30 | 115964.0 |
247 rows × 1 columns
Para descobrir o drawdown anual do período estabelecido, precisamos realizar os seguintes passos:
- Identificar quais os anos estão compreendidos entre nossas datas inicial e final;
- Iterar sobre cada um dos anos e filtrar apenas os dados para aquele ano;
- Calcular o drawdown para o dataframe filtrado.
Vamos construir uma lista com os anos entre start_date e end_date:
from datetime import datetime
start = datetime.strptime(start_date, "%Y-%m-%d")
end = datetime.strptime(end_date, "%Y-%m-%d")
years = range(start.year, end.year + 1)
list(years)[2015, 2016, 2017, 2018, 2019, 2020]Com a lista definida, vamos iterar sobre cada ano, filtrar os dados necessários e adicionar o drawdown do ano em um dicionário:
drawdowns = {}
for year in years:
yearly_data = data[data.index.year == year].copy()
yearly_drawdown = get_drawdown(yearly_data)
drawdowns[year] = yearly_drawdown
drawdowns
{2015: 25.583959208985046, 2016: 12.035425490951097, 2017: 12.00544517175462, 2018: 20.35070105986104, 2019: 10.00160009600576, 2020: 46.815808848136}Pronto! Temos todos os drawdowns do Ibovespa nos últimos 5 anos de forma extremamente simples.
Calculando o drawdown de diversos ativos
Nós mencionamos anteriormente que o drawdown pode ser utilizado como uma medida comparativa entre duas estratégias de investimento. Sendo assim, é bastante útil colocar o drawdown em contexto.
Agora que calculamos o drawdown do Ibovespa nos últimos 5 anos, podemos repetir o raciocínio para diversos outros papeis da bolsa. No entanto, em vez de fazermos isso manualmente, vamos escrever um código que nos possibilite compará-los de forma bastante objetiva:
# Arbitrary list of stocks
tickers = [
"^BVSP",
"PETR4.SA",
"VALE3.SA",
"VVAR3.SA",
"EQTL3.SA",
"LREN3.SA",
"GOLL4.SA",
"BTOW3.SA",
"WEGE3.SA",
"ITUB4.SA",
"BBAS3.SA",
"B3SA3.SA",
"MOVI3.SA",
"AZUL4.SA",
"IRBR3.SA"
]
stocks = yf.download(tickers, start=start_date, end=end_date).copy()['Adj Close']
stocks| AZUL4.SA | B3SA3.SA | BBAS3.SA | BTOW3.SA | EQTL3.SA | GOLL4.SA | IRBR3.SA | ITUB4.SA | LREN3.SA | MOVI3.SA | PETR4.SA | VALE3.SA | VVAR3.SA | WEGE3.SA | ^BVSP | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Date | |||||||||||||||
| 2015-01-02 | NaN | 7.692603 | 16.429703 | 21.140301 | 3.882352 | 14.990000 | NaN | 13.516544 | 10.508009 | NaN | 8.683293 | 17.272886 | 6.543556 | 10.323507 | 48512.0 |
| 2015-01-05 | NaN | 7.482286 | 16.088779 | 20.464600 | 3.734117 | 14.850000 | NaN | 13.584496 | 10.215857 | NaN | 7.941135 | 17.013140 | 6.543556 | 10.393835 | 47517.0 |
| 2015-01-06 | NaN | 7.555089 | 16.313652 | 20.522499 | 3.944471 | 15.210000 | NaN | 13.804224 | 10.333539 | NaN | 7.681378 | 17.694967 | 6.543556 | 10.239674 | 48001.0 |
| 2015-01-07 | NaN | 7.854380 | 17.031767 | 20.319799 | 3.910589 | 14.550000 | NaN | 14.303653 | 10.509348 | NaN | 8.043181 | 18.344326 | 7.082436 | 10.122375 | 49463.0 |
| 2015-01-08 | NaN | 7.749222 | 17.089794 | 19.653799 | 3.882352 | 14.270000 | NaN | 14.527440 | 10.521830 | NaN | 8.562695 | 18.539129 | 7.082436 | 10.293266 | 49943.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2020-12-22 | 35.270000 | 59.737888 | 38.290001 | 75.970001 | 22.650000 | 23.299999 | 7.19 | 31.235180 | 43.160000 | 19.208057 | 27.280001 | 86.940002 | 15.940000 | 72.820000 | 116348.0 |
| 2020-12-23 | 37.700001 | 59.450500 | 38.919998 | 75.599998 | 22.670000 | 24.540001 | 7.24 | 31.924854 | 43.720001 | 19.823507 | 27.950001 | 87.360001 | 16.129999 | 72.620003 | 117857.0 |
| 2020-12-28 | 37.770000 | 60.946918 | 39.349998 | 77.040001 | 23.040001 | 24.250000 | 8.11 | 32.154743 | 43.970001 | 19.892996 | 28.180000 | 87.309998 | 16.590000 | 75.500000 | 119051.0 |
| 2020-12-29 | 37.669998 | 61.264038 | 39.119999 | 75.699997 | 22.980000 | 24.480000 | 8.21 | 32.084778 | 44.130001 | 20.031967 | 28.270000 | 87.070000 | 16.580000 | 75.150002 | 119475.0 |
| 2020-12-30 | 39.299999 | 61.422600 | 38.799999 | 75.610001 | 23.160000 | 24.940001 | 8.18 | 31.615000 | 43.540001 | 20.498520 | 28.340000 | 87.449997 | 16.160000 | 75.739998 | 119306.0 |
1489 rows × 15 columns
O raciocínio é o mesmo: iteraremos sobre a lista de ativos e calcularemos o drawdown anual, armazenando essa informação em um dicionário. Eis o código:
all_drawdowns = {}
for ticker in tickers:
data = stocks[[ticker]]
drawdowns = {}
for year in years:
yearly_data = data[data.index.year == year].copy()
yearly_drawdown = get_drawdown(yearly_data, column = ticker)
drawdowns[year] = yearly_drawdown
all_drawdowns[ticker] = drawdowns
all_drawdowns
{'^BVSP': {2015: 25.583959208985046, 2016: 12.035425490951097, 2017: 12.00544517175462, 2018: 20.35070105986104, 2019: 10.00160009600576, 2020: 46.815808848136}, 'PETR4.SA': {2015: 55.370760542208906, 2016: 38.864638802102405, 2017: 27.656924921683206, 2018: 46.95510222158168, 2019: 17.24379544534969, 2020: 63.35605336711879}, 'VALE3.SA': {2015: 56.08258065080083, 2016: 35.56986161485101, 2017: 28.093024393482068, 2018: 20.418006567945692, 2019: 25.93054585334471, 2020: 40.550904946181845}, 'VVAR3.SA': {2015: 82.87937752873043, 2016: 27.113703092645718, 2017: 27.897840647678603, 2018: 50.44702954161212, 2019: 36.000001430511475, 2020: 75.36057659242984}, 'EQTL3.SA': {2015: 14.331557740431938, 2016: 11.292590784644522, 2017: 11.805536665040066, 2018: 21.719273446438702, 2019: 11.631328831997262, 2020: 40.9665448071925}, 'LREN3.SA': {2015: 28.140179772014978, 2016: 21.70930481448726, 2017: 13.185765146517658, 2018: 27.71149584936101, 2019: 10.916516169469098, 2020: 50.61581662818844}, 'GOLL4.SA': {2015: 84.28665286712683, 2016: 53.83693244372522, 2017: 35.822224087185326, 2018: 61.02971679584582, 2019: 33.202998881506915, 2020: 85.65941097556318}, 'BTOW3.SA': {2015: 51.53851005883385, 2016: 44.8766768778324, 2017: 37.82624008178883, 2018: 28.102685346893097, 2019: 40.610198199484834, 2020: 45.63492063492063}, 'WEGE3.SA': {2015: 29.04629568162771, 2016: 20.417983053408694, 2017: 14.691519912317894, 2018: 23.65182624442001, 2019: 12.363907200496495, 2020: 46.66773431693059}, 'ITUB4.SA': {2015: 25.684997781423753, 2016: 19.146231930567005, 2017: 15.206064144768739, 2018: 28.817874021335587, 2019: 18.424106664124775, 2020: 45.213991230064984}, 'BBAS3.SA': {2015: 46.03704780847024, 2016: 30.13645556938046, 2017: 27.294988974337496, 2018: 43.24986947539893, 2019: 20.929829022200064, 2020: 58.286981851334964}, 'B3SA3.SA': {2015: 20.408398517908605, 2016: 25.492304232567232, 2017: 13.647302811687819, 2018: 29.13132745018055, 2019: 14.231530205537815, 2020: 42.687741180836376}, 'MOVI3.SA': {2015: nan, 2016: nan, 2017: 39.285931215455165, 2018: 40.5945655236307, 2019: 20.034250511972054, 2020: 65.71809662426533}, 'AZUL4.SA': {2015: nan, 2016: nan, 2017: 17.14285488927662, 2018: 47.19565512966372, 2019: 24.91710126385561, 2020: 83.41611855988668}, 'IRBR3.SA': {2015: nan, 2016: nan, 2017: 6.0834261004924155, 2018: 9.88859148803348, 2019: 15.05290894618084, 2020: 87.41285870315963}}
Os drawdowns estão calculados mas a visualização não é das melhores. Vamos criar um dataframe onde os ativos estarão nas linhas e cada ano será uma nova coluna:
table = pd.DataFrame(columns=years, index=tickers)
table
| 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | |
|---|---|---|---|---|---|---|
| ^BVSP | NaN | NaN | NaN | NaN | NaN | NaN |
| PETR4.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| VALE3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| VVAR3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| EQTL3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| LREN3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| GOLL4.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| BTOW3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| WEGE3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| ITUB4.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| BBAS3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| B3SA3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| MOVI3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| AZUL4.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| IRBR3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
O próximo passo é preencher o dataframe com os valores do dicionário calculado anteriormente:
for ticker in all_drawdowns:
table.loc[ticker] = all_drawdowns[ticker]
table
| 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | |
|---|---|---|---|---|---|---|
| ^BVSP | 25.584 | 12.0354 | 12.0054 | 20.3507 | 10.0016 | 46.8158 |
| PETR4.SA | 55.3708 | 38.8646 | 27.6569 | 46.9551 | 17.2438 | 63.3561 |
| VALE3.SA | 56.0826 | 35.5699 | 28.093 | 20.418 | 25.9305 | 40.5509 |
| VVAR3.SA | 82.8794 | 27.1137 | 27.8978 | 50.447 | 36 | 75.3606 |
| EQTL3.SA | 14.3316 | 11.2926 | 11.8055 | 21.7193 | 11.6313 | 40.9665 |
| LREN3.SA | 28.1402 | 21.7093 | 13.1858 | 27.7115 | 10.9165 | 50.6158 |
| GOLL4.SA | 84.2867 | 53.8369 | 35.8222 | 61.0297 | 33.203 | 85.6594 |
| BTOW3.SA | 51.5385 | 44.8767 | 37.8262 | 28.1027 | 40.6102 | 45.6349 |
| WEGE3.SA | 29.0463 | 20.418 | 14.6915 | 23.6518 | 12.3639 | 46.6677 |
| ITUB4.SA | 25.685 | 19.1462 | 15.2061 | 28.8179 | 18.4241 | 45.214 |
| BBAS3.SA | 46.037 | 30.1365 | 27.295 | 43.2499 | 20.9298 | 58.287 |
| B3SA3.SA | 20.4084 | 25.4923 | 13.6473 | 29.1313 | 14.2315 | 42.6877 |
| MOVI3.SA | NaN | NaN | 39.2859 | 40.5946 | 20.0343 | 65.7181 |
| AZUL4.SA | NaN | NaN | 17.1429 | 47.1957 | 24.9171 | 83.4161 |
| IRBR3.SA | NaN | NaN | 6.08343 | 9.88859 | 15.0529 | 87.4129 |
Muito melhor! O último passo é criar uma coluna para a média simples dos drawdowns e ordenar da menor média para a maior:
table["Average"] = table.mean(axis=1)
table = table.sort_values("Average")
table
| 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | Average | |
|---|---|---|---|---|---|---|---|
| EQTL3.SA | 14.3316 | 11.2926 | 11.8055 | 21.7193 | 11.6313 | 40.9665 | 18.624472 |
| ^BVSP | 25.584 | 12.0354 | 12.0054 | 20.3507 | 10.0016 | 46.8158 | 21.132157 |
| B3SA3.SA | 20.4084 | 25.4923 | 13.6473 | 29.1313 | 14.2315 | 42.6877 | 24.266434 |
| WEGE3.SA | 29.0463 | 20.418 | 14.6915 | 23.6518 | 12.3639 | 46.6677 | 24.473211 |
| LREN3.SA | 28.1402 | 21.7093 | 13.1858 | 27.7115 | 10.9165 | 50.6158 | 25.379846 |
| ITUB4.SA | 25.685 | 19.1462 | 15.2061 | 28.8179 | 18.4241 | 45.214 | 25.415544 |
| IRBR3.SA | NaN | NaN | 6.08343 | 9.88859 | 15.0529 | 87.4129 | 29.609446 |
| VALE3.SA | 56.0826 | 35.5699 | 28.093 | 20.418 | 25.9305 | 40.5509 | 34.440821 |
| BBAS3.SA | 46.037 | 30.1365 | 27.295 | 43.2499 | 20.9298 | 58.287 | 37.655862 |
| MOVI3.SA | NaN | NaN | 39.2859 | 40.5946 | 20.0343 | 65.7181 | 41.408211 |
| BTOW3.SA | 51.5385 | 44.8767 | 37.8262 | 28.1027 | 40.6102 | 45.6349 | 41.431539 |
| PETR4.SA | 55.3708 | 38.8646 | 27.6569 | 46.9551 | 17.2438 | 63.3561 | 41.574546 |
| AZUL4.SA | NaN | NaN | 17.1429 | 47.1957 | 24.9171 | 83.4161 | 43.167932 |
| VVAR3.SA | 82.8794 | 27.1137 | 27.8978 | 50.447 | 36 | 75.3606 | 49.949755 |
| GOLL4.SA | 84.2867 | 53.8369 | 35.8222 | 61.0297 | 33.203 | 85.6594 | 58.972989 |
Considerações finais
- O drawdown é uma forma de expor a volatilidade de um ativo. Note que mesmo em um ano relativamente calmo e direcional para a bolsa como 2019, ativos como GOLL4 e BTOW3 chacoalharam bastante. Em contrapartida, EQTL3 costuma ser bastante estável e mesmo em um ano de queda brutal como 2020, ela teve o menor drawdown da lista;
- IRBR3, AZUL4 e MOVI3 fizeram seu IPO em 2017 e portanto não possuem drawdown antes disso;
- A média é apenas uma pista, mas não conta a história toda. Note como IRBR3 possuía uma média extremamente baixa até o ano de 2020, onde apresentou o maior tombo de todos (inclusive maior que as aéreas!)
Agora que já sabemos calcular o drawdown podemos utilizar essa medida nas nossas estratégias de trade. Fique ligado para os próximos posts, onde compareremos estratégias não somente no seu retorno financeiro, mas no seu drawdown máximo.
Inscreva-se no canal do QuantBrasil!
Acompanhe novidades sobre a plataforma, vídeos sobre finanças quantitativas, tutoriais sobre programação e Inteligência Artificial!