Backtest da Estratégia de IFR2 Utilizando Médias Móveis Como Filtro
A estratégia de IFR2 é um modelo de volatilidade, onde geralmente não se leva em consideração a tendência em que o ativo se encontra. Entretanto, se considerarmos que a estratégia se aplica na ponta da compra, operar um ativo em tendência de alta não melhoraria nossos resultados? Pensando nisso, no post de hoje nós faremos o backtest da estratégia de IFR2 utilizando filtros através das médias móveis.
Médias Móveis
A média móvel representa a média dos preços de fechamento dos últimos candles em um determinado período. Por conta disso, ela é muito utilizada na análise técnica para indicar a tendência do papel.
Nós utilizaremos médias móveis mais longas, uma vez que o ponto de entrada da estratégia se dá quando o indicador está abaixo 30, e um papel sobrevendido dificilmente estará em tendência de alta num período mais curto. As médias móveis serão de dois tipos:
- aritméticas de 200 e 50 períodos;
- e exponencial de 80 períodos.
O backtest
O backtest que implementaremos terá como ponto de entrada:
- o preço de fechamento quando o IFR2 for menor ou igual a 30;
- e a média móvel estiver subindo.
Testaremos para dois pontos de saída diferentes:
- máxima dos dois dias anteriores;
- IFR2 maior ou igual a 70 com e sem stop de 7 dias.
Agora que já demos uma geral no conceito de média móvel e na estratégia que iremos testar, vamos trabalhar!
Importando as bibliotecas e baixando os dados necessários
Como de costume, o primeiro passo é importar as bibliotecas de interesse e baixar os dados necessários.
# %%capture means we suppress the output
%%capture
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
!pip install yfinance
import yfinance as yfdf = yf.download("LREN3.SA", start="2015-01-01", end="2020-12-30").copy()[["Open", "High", "Close"]][*********************100%***********************] 1 of 1 completed
Calculando o IFR para 2 períodos
Em seguida, calcularemos o IFR para 2 períodos através da nossa função rsi() e , logo depois, adicionaremos os valores calculados à uma nova coluna df["IFR2"].
def rsi(data, column, window=2):
data = data.copy()
# Establish gains and losses for each day
data["Variation"] = data[column].diff()
data = data[1:]
data["Gain"] = np.where(data["Variation"] > 0, data["Variation"], 0)
data["Loss"] = np.where(data["Variation"] < 0, data["Variation"], 0)
# Calculate simple averages so we can initialize the classic averages
simple_avg_gain = data["Gain"].rolling(window).mean()
simple_avg_loss = data["Loss"].abs().rolling(window).mean()
classic_avg_gain = simple_avg_gain.copy()
classic_avg_loss = simple_avg_loss.copy()
for i in range(window, len(classic_avg_gain)):
classic_avg_gain[i] = (classic_avg_gain[i - 1] * (window - 1) + data["Gain"].iloc[i]) / window
classic_avg_loss[i] = (classic_avg_loss[i - 1] * (window - 1) + data["Loss"].abs().iloc[i]) / window
# Calculate the RSI
RS = classic_avg_gain / classic_avg_loss
RSI = 100 - (100 / (1 + RS))
return RSIdf["IFR2"] = rsi(df, column="Close")
df.head()| Open | High | Close | IFR2 | |
|---|---|---|---|---|
| Date | ||||
| 2015-01-02 | 12.497520 | 12.575206 | 12.545454 | NaN |
| 2015-01-05 | 12.467768 | 12.467768 | 12.196694 | NaN |
| 2015-01-06 | 12.148760 | 12.457851 | 12.337190 | 28.716173 |
| 2015-01-07 | 12.376859 | 12.661157 | 12.547107 | 61.636362 |
| 2015-01-08 | 12.495867 | 12.644628 | 12.561983 | 63.993226 |
Calculando as Médias Móveis
Além do IFR, vamos calcular as médias móveis, que também serão utilizadas para estabelecer as regras de operação.
Para o cálculo das médias móveis aritméticas de 200 e 50 períodos, utilizaremos a função rolling(). Já a média móvel exponencial de 80 períodos será calculada através da função ewm(). Em ambos os casos, incluiremos a função mean() ao final, que irá enfim calcular a média do conjunto de valores pré-selecionados.
# arithmetic moving average calculation
df["MMA200"] = df["Close"].rolling(200).mean()
df["MMA50"] = df["Close"].rolling(50).mean()
#e xponential moving average calculation
df['MME80'] = df["Close"].ewm(span=80).mean()
df.tail()| Open | High | Close | IFR2 | MMA200 | MMA50 | MME80 | |
|---|---|---|---|---|---|---|---|
| Date | |||||||
| 2020-12-21 | 44.259998 | 45.040001 | 43.950001 | 7.152932 | 41.28020 | 43.6696 | 43.658900 |
| 2020-12-22 | 44.000000 | 44.389999 | 43.160000 | 3.737608 | 41.23700 | 43.7346 | 43.646581 |
| 2020-12-23 | 43.160000 | 43.950001 | 43.720001 | 42.595821 | 41.20170 | 43.8248 | 43.648394 |
| 2020-12-28 | 43.689999 | 43.990002 | 43.970001 | 57.804029 | 41.19155 | 43.9070 | 43.656335 |
| 2020-12-29 | 43.959999 | 44.310001 | 44.130001 | 68.489606 | 41.16095 | 44.0066 | 43.668030 |
Pronto! Com os valores das médias móveis, vamos calcular a variação de cada uma, pois assim saberemos se ela está subindo (variação > 0) ou não. Utilizaremos a função pct_change(), que calcula, por padrão, a variação percentual da linha imediatamente anterior. Armazenaremos essas informações em novas colunas.
# percentage change calculation
df["Variation 200"] = df["MMA200"].pct_change()
df["Variation 50"] = df["MMA50"].pct_change()
df["Variation 80"] = df["MME80"].pct_change()
# We don't need them anymore
df.drop(columns=["MMA200", "MMA50", "MME80"], inplace=True)
df.tail()| Open | High | Close | IFR2 | Variation 200 | Variation 50 | Variation 80 | |
|---|---|---|---|---|---|---|---|
| Date | |||||||
| 2020-12-21 | 44.259998 | 45.040001 | 43.950001 | 7.152932 | -0.001282 | 0.001973 | 0.000169 |
| 2020-12-22 | 44.000000 | 44.389999 | 43.160000 | 3.737608 | -0.001047 | 0.001488 | -0.000282 |
| 2020-12-23 | 43.160000 | 43.950001 | 43.720001 | 42.595821 | -0.000856 | 0.002062 | 0.000042 |
| 2020-12-28 | 43.689999 | 43.990002 | 43.970001 | 57.804029 | -0.000246 | 0.001876 | 0.000182 |
| 2020-12-29 | 43.959999 | 44.310001 | 44.130001 | 68.489606 | -0.000743 | 0.002268 | 0.000268 |
Definindo os pontos de entrada e saída
Antes de qualquer coisa, vamos isolar os possíveis pontos de saída dessa estratégia (Target), que corresponde à máxima dos dois dias anteriores. O código é o mesmo do primeiro backtest dessa série.
df["Target1"] = df["High"].shift(1)
df["Target2"] = df["High"].shift(2)
df["Target"] = df[["Target1", "Target2"]].max(axis=1)
# We don't need them anymore
df.drop(columns=["Target1", "Target2"], inplace=True)Para definir os exatos preços de compra e venda, iremos atualizar a função strategy_points(), elaborada no artigo Analisando Diferentes Parâmetros de Entrada para a Estratégia de IFR2. A função receberá 3 argumentos:
- o dataframe (
data); - o valor de IFR de entrada (
rsi_parameter_entry); - e a coluna com a variação da média móvel que irá funcionar como filtro (
variation_column).
O preço de compra ("Buy Price") será estabelecido a partir de duas condições:
- o valor de IFR2 tem que ser menor ou igual a 30 (
condition_1); - e a média móvel tem que estar subindo, ou seja, a variação tem que ser positiva (
condition_2).
Dessa forma, o preço de compra será o preço de fechamento (data["Close"]), se ambas condições forem respeitadas (condition_1 & condition_2). Caso contrário, a linha será preenchida por np.nan.
O preço de venda ("Sell Price") segue a mesma lógica do artigo citado anteriormente.
def strategy_points(data, rsi_parameter_entry, variation_column):
# Define exact buy price
condition_1 = df["IFR2"] <= rsi_parameter_entry
condition_2 = df[variation_column] > 0
data["Buy Price"] = np.where(condition_1 & condition_2, data["Close"], np.nan)
# Define exact sell price
data["Sell Price"] = np.where(
data["High"] > data['Target'],
np.where(data['Open'] > data['Target'], data['Open'], data['Target']),
np.nan)
return data Criando as funções necessárias para o backtest
A função backtest_algorithm() define as regras de operação utilizando os preços de compra e venda determinados pela função anterior. O código a seguir foi desenvolvido no post Backtest da Estratégia de Máximas e Mínimas. A função retorna duas listas:
all_profits, que compreende o lucro de cada operação;- e
total_capital, com o capital acumulado após cada operação.
import math
# Create a function to round any number to the smalles multiple of 100
def round_down(x):
return int(math.floor(x / 100.0)) * 100
def backtest_algorithm(data, initial_capital=10000):
total_capital = [initial_capital] # list with the total capital after every operation
all_profits = [0] # list with profits for every operation
ongoing = False
for i in range(0,len(data)):
if ongoing == True:
if ~(np.isnan(data['Sell Price'][i])):
# Define exit point and total profit
exit = data['Sell Price'][i]
profit = shares * (exit - entry)
# Append profit to list and create a new entry with the capital
# after the operation is complete
all_profits += [profit]
current_capital = total_capital[-1] # current capital is the last entry in the list
total_capital += [current_capital + profit]
ongoing = False
else:
if ~(np.isnan(data['Buy Price'][i])):
entry = data['Buy Price'][i]
shares = round_down(initial_capital / entry)
ongoing = True
return all_profits, total_capitalA função get_drawdown() foi elaborada no post Entenda o Drawdown e Calcule essa Medida de Volatilidade para Qualquer Ativo e retorna o drawdown máximo.
def get_drawdown(data, column = "Close"):
data["Max"] = data[column].cummax()
data["Delta"] = data['Max'] - data[column]
data["Drawdown"] = 100 * (data["Delta"] / data["Max"])
max_drawdown = data["Drawdown"].max()
return max_drawdownA função strategy_test retorna estatísticas do backtest:
- o número total de operações (
num_operation); - o número de operações que deram lucro e prejuízo (
gainselosses); - suas respectivas porcentagens (
pct_gainsepct_losses); - o lucro total (
total_profit); - e o drawdown máximo (
drawdown).
def strategy_test(all_profits, total_capital):
num_operations = (len(all_profits) - 1)
gains = sum(x >= 0 for x in all_profits)
pct_gains = 100 * (gains / num_operations)
losses = num_operations - gains
pct_losses = 100 - pct_gains
total_profit = sum(all_profits)
pct_profit = (total_profit / total_capital[0]) * 100
# Compute drawdown
total_capital = pd.DataFrame(data=total_capital, columns=["total_capital"])
drawdown = get_drawdown(data=total_capital, column="total_capital")
return {
"num_operations": num_operations,
"gains": gains ,
"pct_gains": pct_gains.round(),
"losses": losses,
"pct_losses": pct_losses.round(),
"total_profit": total_profit,
"pct_profit": pct_profit,
"drawdown": drawdown
}Realizando o backtest
Como foi feito nos últimos dois artigos, o último passo do backtest é rodar todas as funções acima em um loop que, nesse caso, irá iterar sobre a lista de médias móveis (periods).
A estatística será armazenada no dicionário statistics e as listas com o lucro e capital acumulado, no dicionário cap_evolution.
periods = [200, 80, 50]
statistics = {}
cap_evolution = {}
for period in periods:
variation_column = "Variation " + str(period)
df = strategy_points(data=df, rsi_parameter_entry=30, variation_column=variation_column)
all_profits, total_capital = backtest_algorithm(df)
statistics[period] = strategy_test(all_profits, total_capital)
key1 = "all_profits_" + str(period)
key2 = "total_capital_" + str(period)
cap_evolution[period] = { key1: all_profits, key2: total_capital }statistics{200: {'num_operations': 95, 'gains': 72, 'pct_gains': 76.0, 'losses': 23, 'pct_losses': 24.0, 'total_profit': 5589.06307220459, 'pct_profit': 55.8906307220459, 'drawdown': 8.879767678840295}, 80: {'num_operations': 98, 'gains': 75, 'pct_gains': 77.0, 'losses': 23, 'pct_losses': 23.0, 'total_profit': 6151.059913635254, 'pct_profit': 61.51059913635254, 'drawdown': 8.501211685719728}, 50: {'num_operations': 100, 'gains': 78, 'pct_gains': 78.0, 'losses': 22, 'pct_losses': 22.0, 'total_profit': 6924.6965408325195, 'pct_profit': 69.2469654083252, 'drawdown': 9.673291514464546}}O próximo passo é transformar o dicionário acima em um dataframe através da função pd.DataFrame.from_dict() e arredondar os valores para duas casa decimais (.round(2)).
statistics = pd.DataFrame.from_dict(statistics, orient="index").round(2)
statistics
| num_operations | gains | pct_gains | losses | pct_losses | total_profit | pct_profit | drawdown | |
|---|---|---|---|---|---|---|---|---|
| 200 | 95 | 72 | 76.0 | 23 | 24.0 | 5589.06 | 55.89 | 8.88 |
| 80 | 98 | 75 | 77.0 | 23 | 23.0 | 6151.06 | 61.51 | 8.50 |
| 50 | 100 | 78 | 78.0 | 22 | 22.0 | 6924.70 | 69.25 | 9.67 |
Plotando as informações mais relevantes
A seguir, utilizaremos a função plot_bars para plotar o número de operações, o lucro e o drawdown em gráficos de barra.
def plot_bars(title, x, y, x_label="IFR2", y_label=None):
fig = plt.figure()
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['top'].set_visible(False)
colors = ["paleturquoise", "mediumturquoise", "darkcyan", "darkslategrey"]
plt.bar(x, y, color=colors)
plt.title(title)
plt.xlabel(x_label)
if y_label != None:
plt.ylabel(y_label)
for i, v in enumerate(y):
plt.text(
x=i,
y=v,
s=str(v),
horizontalalignment='center',
verticalalignment='bottom',
fontdict=dict(fontsize=12)
)x = statistics.index.astype(str)plot_bars(title="Número de Operações", x=x, y=statistics["num_operations"], x_label="Média Móvel")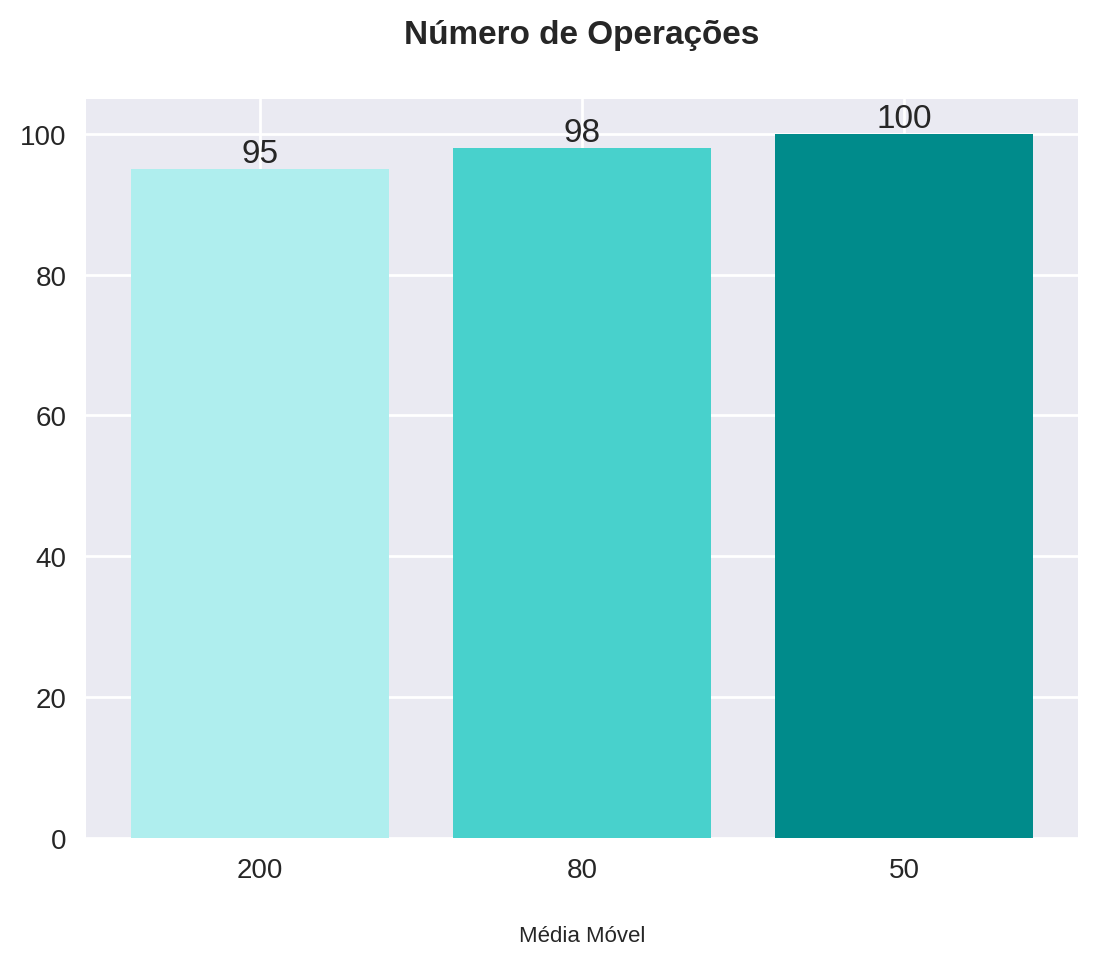
plot_bars(title="Lucro Total (%)", x=x, y=statistics["pct_profit"], x_label="Média Móvel")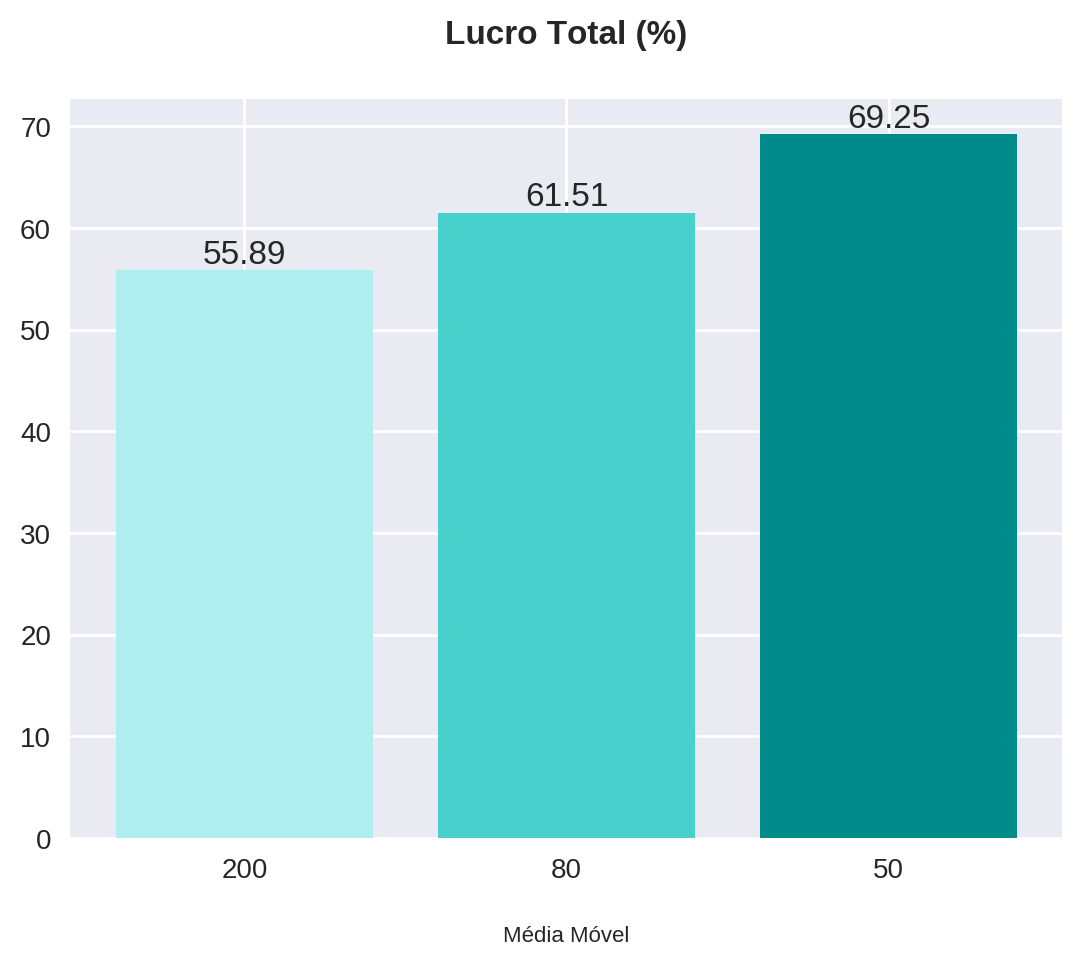
plot_bars(title="Drawdown (%)", x=x, y=statistics["drawdown"], x_label="Média Móvel")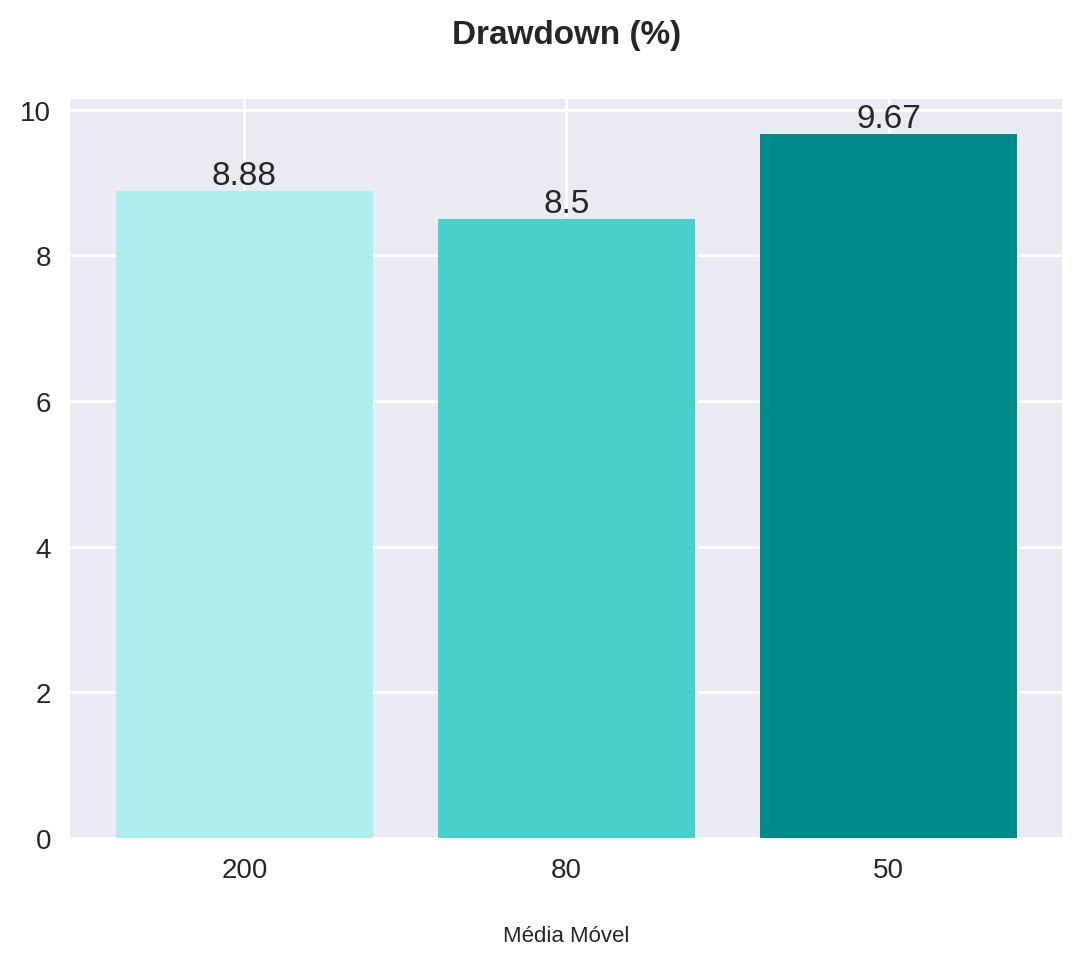
Vamos recapitular os resultados do backtest da estratégia original (sem o filtro de médias móveis), realizado no post Criando o Backtest da Estratégia de IFR2 em Python:
| No. de Operações | Lucro Total (%) | Drawdown Máx. (%) |
|---|---|---|
| 160 | 138,54 | 10,37 |
Agora levando em consideração a tendência:
| Médias Móveis | No. de Operações | Lucro Total (%) | Drawdown Máx. (%) |
|---|---|---|---|
| 200 | 95 | 55,89 | 8,88 |
| 80 | 98 | 61,51 | 8,5 |
| 50 | 100 | 69,25 | 9,67 |
Em relação às três médias móveis, a aritmética de 50 períodos foi a que obteve o melhor lucro. Comparando-a ao backtest da estratégia original (sem filtro), podemos observar que ocorreram menos operações, uma vez que estamos filtrando o nosso ponto de entrada. Já o lucro caiu para praticamente a metade, sem que houvesse uma melhora relevante do drawdown.
Este resultado pode nos levar a interpretações equivocadas, uma vez que o lucro percentual não leva em conta o número de operações. Sendo assim, para uma anáise mais fiel dos resultados, vamos calcular o percentual do lucro por operação.
Calculando o lucro por operação
Faremos isso através de uma função (profit_per_operation) para facilitar o cálculo dos demais backtests. Esta irá receber apenas 2 argumentos:
- o dataframe (
data); - e o nome da estratégia em questão (
strategy_title).
def profit_per_operation(data, strategy_title):
profit = data["pct_profit"] / data["num_operations"]
df = pd.DataFrame(profit).round(2)
df.rename(columns = {0: "profit_per_operation"}, inplace=True)
print(strategy_title, "\n\n", df)profit_per_operation(
statistics,
strategy_title="Entrada em IFR2<=30, saída na máx. dos 2 dias anteriores, sem stop:"
)Entrada em IFR2<=30, saída na máx. dos 2 dias anteriores, sem stop:
profit_per_operation
200 0.59
80 0.63
50 0.69
A estratégia original (sem filtro) apresentou um lucro de 138,54% num universo de 160 operações, o que resulta em um lucro por operação de 0,86% com um drawdown de 10,37%.
Olhando dessa perspectiva, observamos que há uma diferença de aproximadamente 0,2% entre as duas em relação ao lucro por operação. Em termos relativos, essa diferença foi de 20% com uma queda de 6,7% no drawdown. Portanto, nesse backtest a leve melhora do drawdown não compensa a perda de lucratividade.
| Estratégia | Lucro/Operação (%) | Drawdown Máx. (%) |
|---|---|---|
| Original sem filtro | 0,86 | 10,37 |
| Original com filtro MMA50 | 0.69 | 9,67 |
Vamos agora realizar o mesmo backtest, porém com o ponto de saída baseado em valores de IFR2.
Backtest com ponto de saída em IFR2 >= 70
No último artigo Analisando Diferentes Parâmetros de Saída para a Estratégia de IFR2, chegamos à conclusão que alvos em valores de IFR2 maiores ou iguais a 70 e com um stop de 7 dias é a melhor estratégia para quem deseja utilizar o indicador como ponto de saída conciliado a um stop baseado no tempo. Para fins comparativos, testaremos os filtros de médias móveis nessa mesma estratégia com e sem stop.
Sem stop
Vamos atualizar a função strategy_points juntando a lógica do preço de compra elaborada no backtest acima com a lógica do preço de venda escrita no útlimo artigo.
def strategy_points(data, rsi_parameter_entry, rsi_parameter_exit, variation_column):
# Define exact buy price
condition_1 = df["IFR2"] <= rsi_parameter_entry
condition_2 = df[variation_column] > 0
data["Buy Price"] = np.where(condition_1 & condition_2, data["Close"], np.nan)
# Define exact sell price
data["Sell Price"] = np.where(data["IFR2"] >= rsi_parameter_exit, data["Close"], np.nan)
return dataCom os valores exatos de compra e venda, basta rodar a função no loop iterando sobre a lista de médias móveis. Utilizaremos as mesmas funções de simulação da operação (backtest_algorithm) e cálculo da estatística (strategy_test). Os resultados serão armazenados no dicionário backtest.
backtest = {}
for period in periods:
variation_column = "Variation " + str(period)
df = strategy_points(
data=df,
rsi_parameter_entry=30,
rsi_parameter_exit=70,
variation_column=variation_column
)
all_profits, total_capital = backtest_algorithm(df)
backtest[period] = strategy_test(all_profits, total_capital)Transformaremos o backtest em um dataframe e, logo em seguida, plotaremos os dados mais relevantes através da função plot_bars.
backtest = pd.DataFrame.from_dict(backtest, orient="index").round(2)
backtest
| num_operations | gains | pct_gains | losses | pct_losses | total_profit | pct_profit | drawdown | |
|---|---|---|---|---|---|---|---|---|
| 200 | 91 | 69 | 76.0 | 22 | 24.0 | 7584.85 | 75.85 | 9.91 |
| 80 | 89 | 68 | 76.0 | 21 | 24.0 | 7937.71 | 79.38 | 8.51 |
| 50 | 91 | 70 | 77.0 | 21 | 23.0 | 9834.77 | 98.35 | 9.49 |
plot_bars(title="Número de Operações", x=x, y=backtest["num_operations"], x_label="Média Móvel")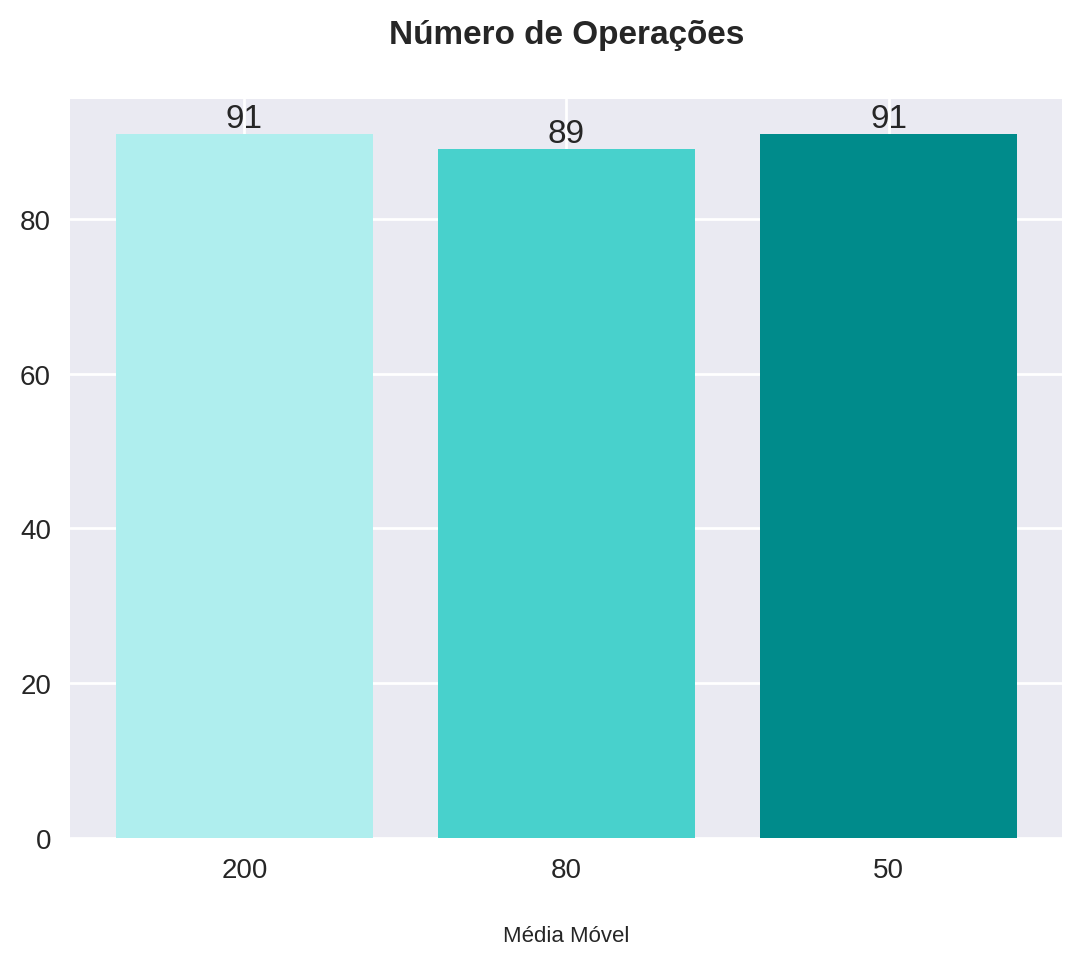
plot_bars(title="Lucro Total (%)", x=x, y=backtest["pct_profit"], x_label="Média Móvel")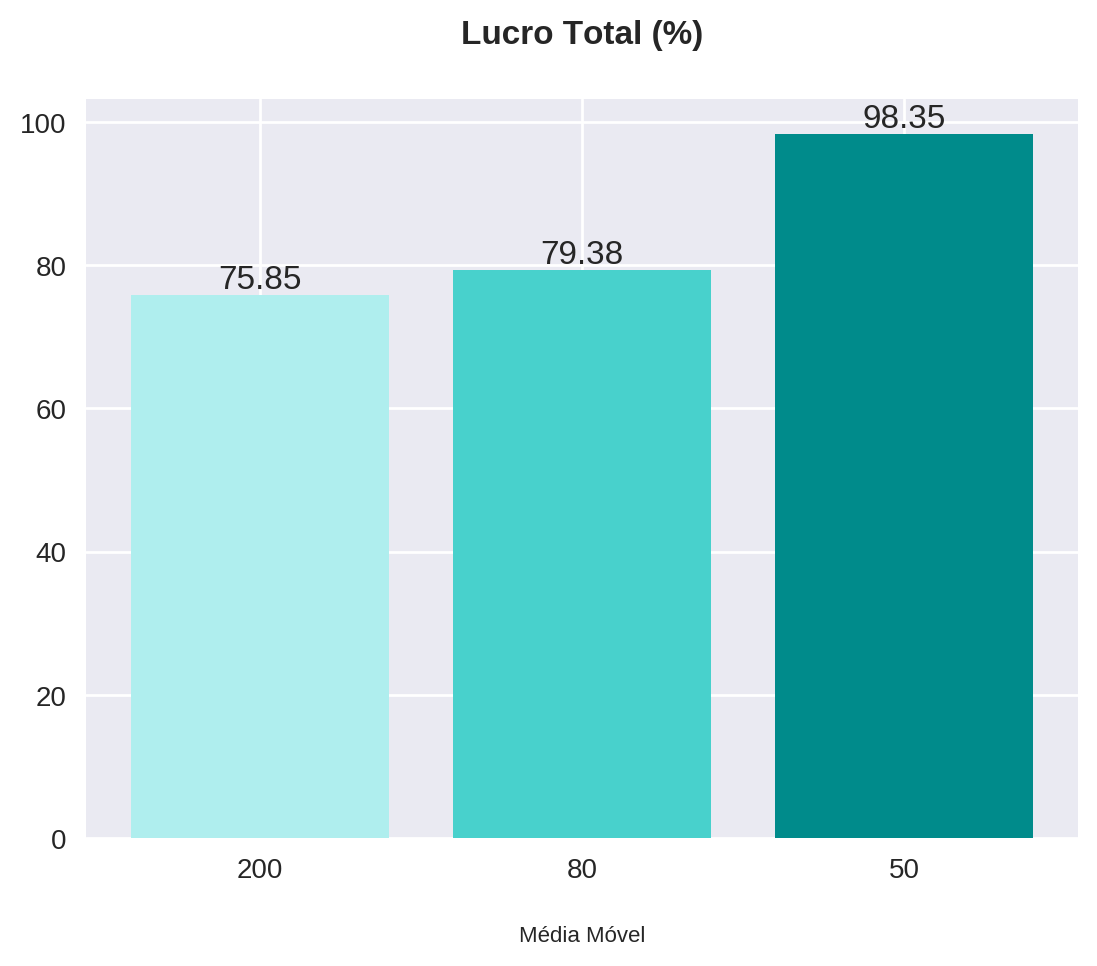
plot_bars(title="Drawdown (%)", x=x, y=backtest["drawdown"], x_label="Média Móvel")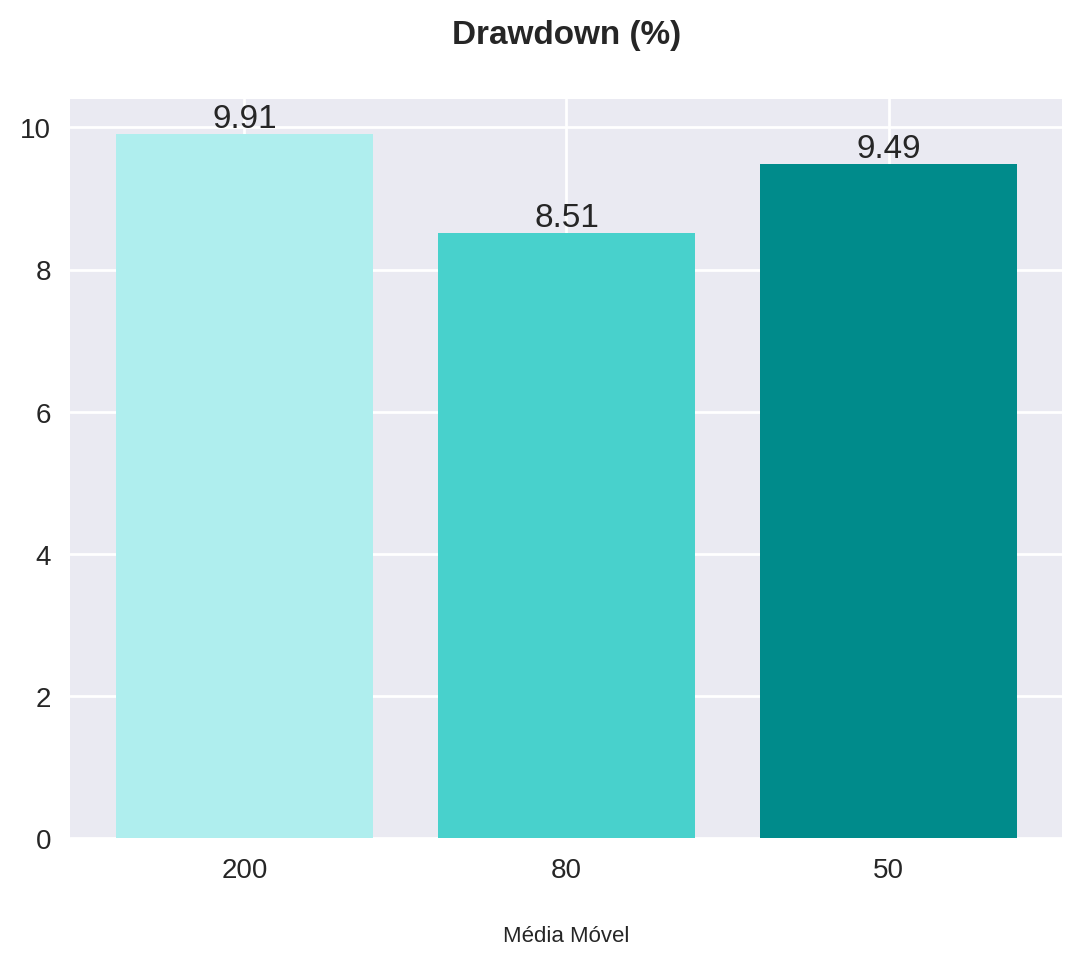
Novamente, os resultados provenientes do filtro com a média móvel aritmética de 50 períodos foram melhores não só em relação às outras médias móveis, mas também comparando com a estratégia anterior (ponto de saída na máxima dos 2 dias anteriores). Isso faz sentido se pensarmos que um ativo em tendência de alta possui mais chances de atingir valores maiores de IFR.
Finalmente, testaremos a mesma estratégia com um stop de 7 dias.
Com stop
Agora vamos realizar o mesmo backtest, porém estabelecendo um stop baseado no tempo. Para isso, utilizaremos a função algorithm_with_stop a seguir.
def algorithm_with_stop(data, max_days, initial_capital=10000):
# List with the total capital after every operation
total_capital = [initial_capital]
# List with profits for every operation. We initialize with 0 so
# both lists have the same size
all_profits = [0]
days_in_operation = 0
ongoing = False
for i in range(0,len(df)):
if ongoing == True:
days_in_operation += 1
# If any of the following conditions are met, the operation will end
if days_in_operation == max_days or ~(np.isnan(df['Sell Price'][i])):
# Define exit point and total profit
exit = np.where(
~(np.isnan(df['Sell Price'][i])),
df['Sell Price'][i],
df['Close'][i])
profit = shares * (exit - entry)
# Append profit to list and create a new entry with the capital
# after the operation is complete
all_profits += [profit]
current_capital = total_capital[-1]
total_capital += [current_capital + profit]
ongoing = False
else:
if ~(np.isnan(df['Buy Price'][i])):
entry = df['Buy Price'][i]
shares = round_down(initial_capital / entry)
days_in_operation = 0
ongoing = True
return all_profits, total_capitalOs próximos passos são os mesmos realizados acima:
backtest_with_stop = {}
for period in periods:
variation_column = "Variation " + str(period)
df = strategy_points(
data=df,
rsi_parameter_entry=30,
rsi_parameter_exit=70,
variation_column=variation_column
)
all_profits, total_capital = algorithm_with_stop(df, max_days=7)
backtest_with_stop[period] = strategy_test(all_profits, total_capital)
backtest_with_stop = pd.DataFrame.from_dict(backtest_with_stop, orient="index").round(2)
backtest_with_stop
| num_operations | gains | pct_gains | losses | pct_losses | total_profit | pct_profit | drawdown | |
|---|---|---|---|---|---|---|---|---|
| 200 | 94 | 71 | 76.0 | 23 | 24.0 | 6876.24 | 68.76 | 12.83 |
| 80 | 94 | 71 | 76.0 | 23 | 24.0 | 8053.43 | 80.53 | 10.10 |
| 50 | 96 | 73 | 76.0 | 23 | 24.0 | 10033.38 | 100.33 | 11.31 |
plot_bars(title="Número de Operações", x=x, y=backtest_with_stop["num_operations"], x_label="Média Móvel")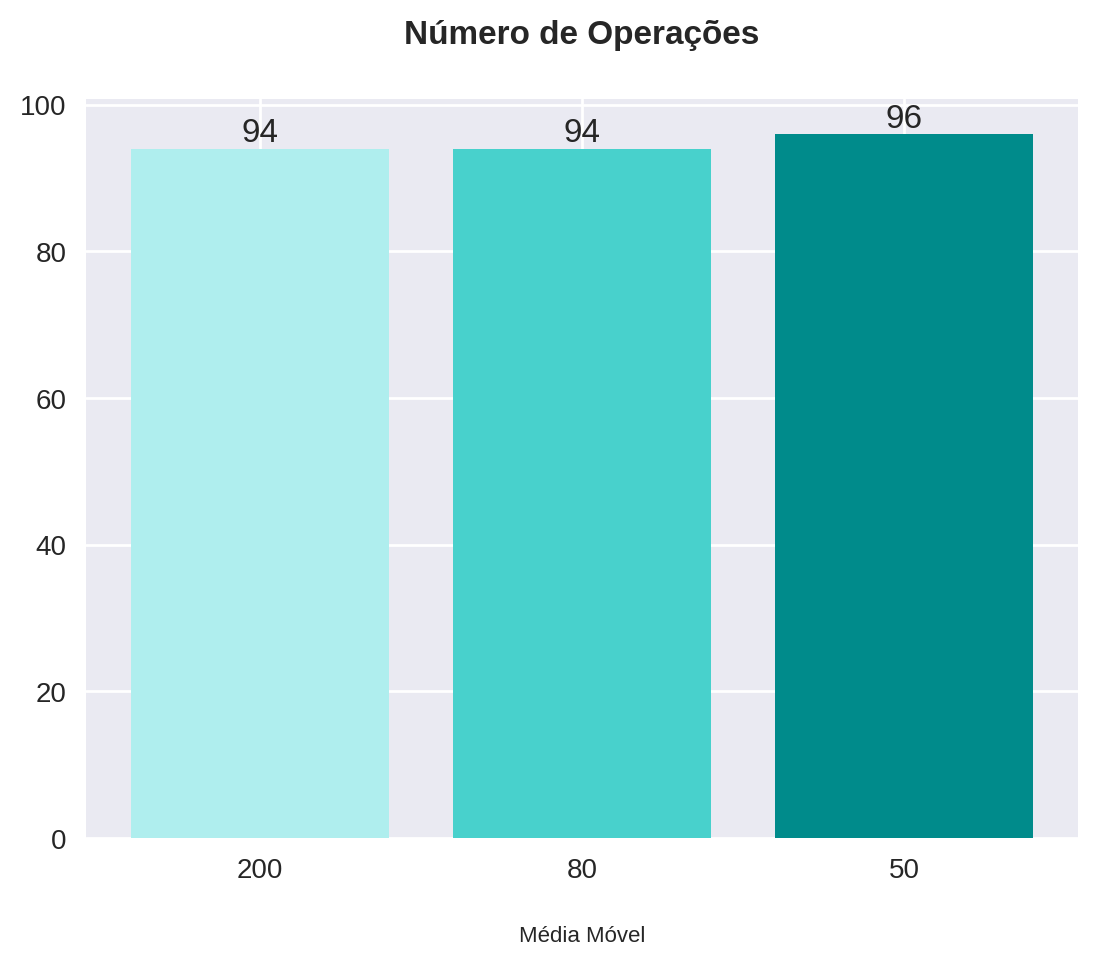
plot_bars(title="Lucro Total (%)", x=x, y=backtest_with_stop["pct_profit"], x_label="Média Móvel")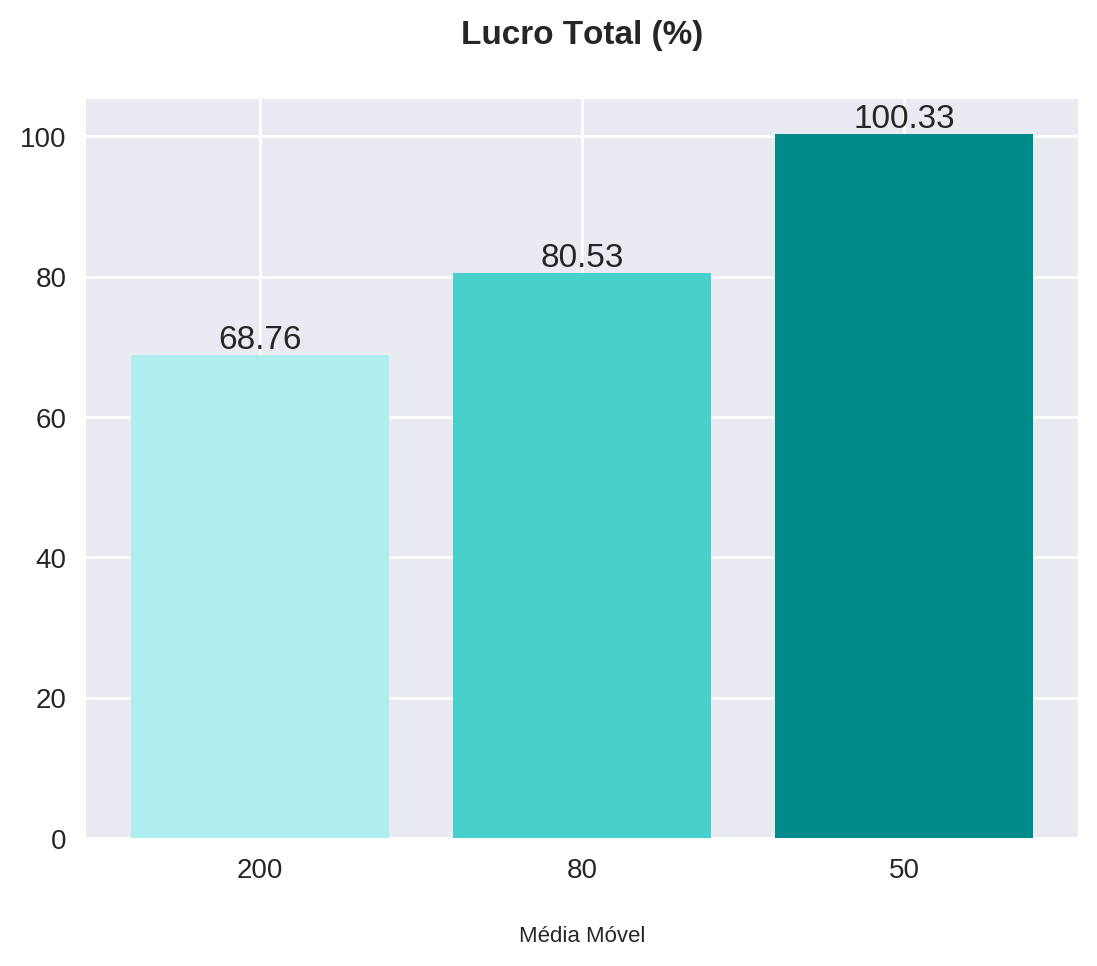
plot_bars(title="Drawdown (%)", x=x, y=backtest_with_stop["drawdown"], x_label="Média Móvel")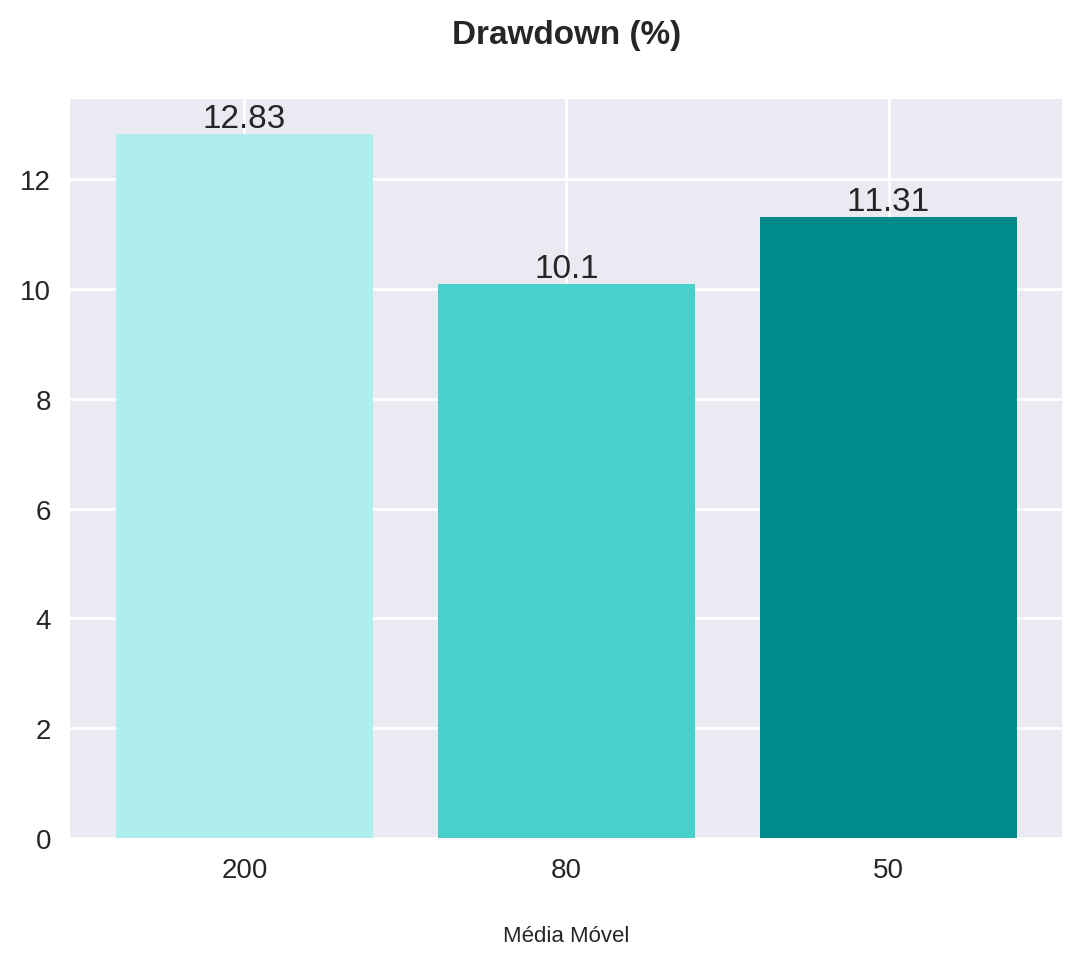
De maneira semelhante, a média móvel aritmética de 50 períodos foi a que performou melhor entre as três tanto com, quanto sem stop... mas nossa análise não para por aí!
Calculando o lucro por operação
profit_per_operation(backtest, strategy_title="Entrada em IFR2 <= 30, saída em IFR2 >= 70, sem stop:")Entrada em IFR2 <= 30, saída em IFR2 >= 70, sem stop:
profit_per_operation
200 0.83
80 0.89
50 1.08
profit_per_operation(backtest_with_stop, strategy_title="Entrada em IFR2 <= 30, saída em IFR2 >= 70, stop de 7 dias:")Entrada em IFR2 <= 30, saída em IFR2 >= 70, stop de 7 dias:
profit_per_operation
200 0.73
80 0.86
50 1.05
Mais uma vez, a estratégia utilizando a média móvel aritmética de 50 períodos performou melhor em relação às outras. Por conta disso, analisaremos apenas os resultados dela para os 3 backtests realizados aqui.
| Estratégia | Lucro/Operação (%) | Lucro Total (%) | Drawdown Máx. (%) |
|---|---|---|---|
| Máx. 2 dias (sem filtro) | 0,86 | 138,54% | 10,37 |
| Máx. 2 dias | 0,69 | 69,25 | 9,67 |
| IFR2 >= 70 | 1.08 | 98,35 | 9,49 |
| IFR2 >= 70 (com stop) | 1.04 | 100,33 | 11,31 |
Apesar de valores semelhantes, a estratégia sem o stop resultou em uma maior porcentagem de lucro/operação e menor drawdown. Uma explicação é que uma vez que o filtro garante que o papel esteja em tendência de alta, há pouca vantagem em se adicionar o stop no tempo.
Conclusão
De acordo com nossas análises, observamos duas estratégias plausíveis para o IFR2:
- Sem considerar a tendência: opera-se todas as entradas que o IFR2 menor ou iguais a 30 ativar.
- Considerando a tendência: realiza-se uma pré-seleção das entradas através de uma média móvel mais longa.
Agora que nós já testamos a estratégia de IFR2 em diversos cenários e chegamos a essas duas vertentes, o próximo passo é fazer o backtest em diversos ativos. Sendo assim, no próximo post iremos finalizar essa série de artigos analisando como selecionar os melhores ativos para a estratégia.
Inscreva-se no canal do QuantBrasil!
Acompanhe novidades sobre a plataforma, vídeos sobre finanças quantitativas, tutoriais sobre programação e Inteligência Artificial!