Criando o Backtest da Estratégia de IFR2 em Python
No primeiro artigo dessa série sobre o IFR (Aprenda a Calcular o IFR — Índice de Força Relativa), discutimos sobre o indicador e criamos uma função para calculá-lo e plotá-lo utilizando pandas e matplotlib. Hoje, daremos prosseguimento a esse código para realizar o backtest da estratégia de IFR2. Então, se você ainda não leu o primeiro artigo dessa série, aproveite para ler antes de continuarmos!
Caso ainda não tenha lido, aproveite a oportunidade para conferir o post sobre o Backtest da Estratégia de Máximas e Mínimas, uma vez que grande parte da lógica dos dois algoritmos é semelhante.
A estratégia
O IFR2 nada mais é do que o Índice de Força Relativa calculado para 2 períodos. Esse setup é amplamente utilizado por apresentar altas taxas de acertos (até 80%) e ser bastante consistente na análise técnica.
A estratégia de IFR2 que iremos testar aqui seguirá o seguinte conjunto de regras:
- Tipo de gráfico: diário;
- Tipo de operação: ponta da compra;
- Ponto de entrada: abaixo ou igual a um valor de IFR2 de 30, comprando no preço de fechamento;
- Ponto de Saída: alvo na máxima dos dois dias anteriores (alvo móvel);
- Stop Loss: muitos traders realizam o setup sem stop, aqui nós vamos testá-lo tanto sem, como com um stop no tempo.
Importando as bibliotecas
Como de praxe, o primeiro passo é importar as bibliotecas de interesse.
# %%capture means we suppress the output
%%capture
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
!pip install yfinance
import yfinance as yfDownload da base de dados
O próximo passo é fazer o download de um ativo qualquer em um período arbitrário.
Repare que nós faremos uma cópia do dataframe, para então selecionar somente as colunas desejadas. Isso evita o aviso de "SettingWithCopyWarning", onde o pandas alerta que uma modificação está sendo feita em uma fatia (slice) do dataframe, o que pode levar a erros difíceis de serem identificados. Recomendo a leitura desse artigo para entender mais sobre o motivo desse aviso.
df = yf.download("LREN3.SA", start="2015-01-01", end="2020-12-30").copy()[["Open", "High", "Close", "Adj Close"]]
df.head()[*********************100%***********************] 1 of 1 completed
| Open | High | Close | Adj Close | |
|---|---|---|---|---|
| Date | ||||
| 2015-01-02 | 12.4975 | 12.5752 | 12.5455 | 10.508009 |
| 2015-01-05 | 12.4678 | 12.4678 | 12.1967 | 10.215857 |
| 2015-01-06 | 12.1488 | 12.4579 | 12.3372 | 10.333539 |
| 2015-01-07 | 12.3769 | 12.6612 | 12.5471 | 10.509348 |
| 2015-01-08 | 12.4959 | 12.6446 | 12.5620 | 10.521830 |
Calculando o IFR para 2 períodos
Para o cálculo do IFR, vamos utilizar uma versão simplificada da função que desenvolvemos na parte 1 dessa série. Em particular, estamos interessados apenas em retornar o valor do IFR de 2 períodos para o ativo desejado em qualquer momento no tempo.
def rsi(data, column, window=2):
data = data.copy()
# Establish gains and losses for each day
data["Variation"] = data[column].diff()
data = data[1:]
data["Gain"] = np.where(data["Variation"] > 0, data["Variation"], 0)
data["Loss"] = np.where(data["Variation"] < 0, data["Variation"], 0)
# Calculate simple averages so we can initialize the classic averages
simple_avg_gain = data["Gain"].rolling(window).mean()
simple_avg_loss = data["Loss"].abs().rolling(window).mean()
classic_avg_gain = simple_avg_gain.copy()
classic_avg_loss = simple_avg_loss.copy()
for i in range(window, len(classic_avg_gain)):
classic_avg_gain[i] = (classic_avg_gain[i - 1] * (window - 1) + data["Gain"].iloc[i]) / window
classic_avg_loss[i] = (classic_avg_loss[i - 1] * (window - 1) + data["Loss"].abs().iloc[i]) / window
# Calculate the RSI
RS = classic_avg_gain / classic_avg_loss
RSI = 100 - (100 / (1 + RS))
return RSIEm seguida, criaremos uma nova coluna com os valores do IFR2 gerados pela função acima.
df["IFR2"] = rsi(df, column="Adj Close")
df.head()| Open | High | Close | Adj Close | IFR2 | |
|---|---|---|---|---|---|
| Date | |||||
| 2015-01-02 | 12.4975 | 12.5752 | 12.5455 | 10.508009 | NaN |
| 2015-01-05 | 12.4678 | 12.4678 | 12.1967 | 10.215857 | NaN |
| 2015-01-06 | 12.1488 | 12.4579 | 12.3372 | 10.333539 | 28.714604 |
| 2015-01-07 | 12.3769 | 12.6612 | 12.5471 | 10.509348 | 61.632231 |
| 2015-01-08 | 12.4959 | 12.6446 | 12.5620 | 10.521830 | 63.993122 |
Definindo o alvo
A partir daqui, o código é bem similar ao da Estratégia de Máximas e Mínimas — quem leu o post vai tirar de letra!
Antes de utilizarmos o algoritmo que irá simular as operações, nós temos que determinar os possíveis pontos de entrada e saída. Como nosso alvo é a máxima dos dois dias anteriores, nós primeiro isolamos essas máximas para então estabelecer qual é a maior entre elas. Armazenaremos esse resultado na coluna Target.
df["Target1"] = df["High"].shift(1)
df["Target2"] = df["High"].shift(2)
df["Target"] = df[["Target1", "Target2"]].max(axis=1)
# We don't need them anymore
df.drop(columns=["Target1", "Target2"], inplace=True)
df.head()| Open | High | Close | Adj Close | IFR2 | Target | |
|---|---|---|---|---|---|---|
| Date | ||||||
| 2015-01-02 | 12.4975 | 12.5752 | 12.5455 | 10.508009 | NaN | NaN |
| 2015-01-05 | 12.4678 | 12.4678 | 12.1967 | 10.215857 | NaN | 12.5752 |
| 2015-01-06 | 12.1488 | 12.4579 | 12.3372 | 10.333539 | 28.714604 | 12.5752 |
| 2015-01-07 | 12.3769 | 12.6612 | 12.5471 | 10.509348 | 61.632231 | 12.4678 |
| 2015-01-08 | 12.4959 | 12.6446 | 12.5620 | 10.521830 | 63.993122 | 12.6612 |
Definindo as regras de operação
Uma vez que nós determinamos nosso ponto de saída, precisamos definir as condições de compra e venda para estabelecer os preços exatos que serão utilizados na simulação pelo algoritmo.
Para isso, vamos criar duas novas colunas com os preços de compra e venda:
- O preço de compra (
Buy Price) será definido como o preço de fechamento (df["Close"]), se o IFR2 for menor ou igual a 30 (rsi_parameter), que é o valor classicamente utilizado para operar essa estratégia. Caso contrário, a linha será preenchida pornp.nan. Note que um trader operando por esse modelo pode realizar a compra alguns minutos antes do fechamento do mercado sem impacto estatístico significativo. - O preço de venda (
Sell Price) é ligeiramente diferente: se a máxima do dia ou o preço de abertura forem maiores que a máxima dos dois dias anteriores, a operação foi para o alvo. No primeiro caso, o preço de venda é o alvo inicial (df['Target']), e no segundo, o preço de abertura (df['Open']). Caso nenhum dos dois aconteça, a linha será preenchida pornp.nan.
# Define exact buy price
rsi_parameter = 30
df["Buy Price"] = np.where(df["IFR2"] <= rsi_parameter, df["Close"], np.nan)
# Define exact sell price
df["Sell Price"] = np.where(
df["High"] > df['Target'],
np.where(df['Open'] > df['Target'], df['Open'], df['Target']),
np.nan)
df.head()| Open | High | Close | Adj Close | IFR2 | Target | Buy Price | Sell Price | |
|---|---|---|---|---|---|---|---|---|
| Date | ||||||||
| 2015-01-02 | 12.4975 | 12.5752 | 12.5455 | 10.508009 | NaN | NaN | NaN | NaN |
| 2015-01-05 | 12.4678 | 12.4678 | 12.1967 | 10.215857 | NaN | 12.5752 | NaN | NaN |
| 2015-01-06 | 12.1488 | 12.4579 | 12.3372 | 10.333539 | 28.714604 | 12.5752 | 12.3372 | NaN |
| 2015-01-07 | 12.3769 | 12.6612 | 12.5471 | 10.509348 | 61.632231 | 12.4678 | NaN | 12.4678 |
| 2015-01-08 | 12.4959 | 12.6446 | 12.5620 | 10.521830 | 63.993122 | 12.6612 | NaN | NaN |
Criando o algoritmo para simular as operações
Agora que nós já temos todas as informações, basta rodar o algoritmo! Como o alvo dessa estratégia também é móvel, o código será exatamente o mesmo criado para o backtest da estratégia de máximas e mínimas. Nele, nós simulamos operações com um capital inicial de R$ 10.000 reais e compramos o máximo de lotes cheios (múltiplos de 100) possíveis.
O código a seguir calcula o capital total acumulado e o lucro de cada operação.
import math
# Create a function to round any number to the smalles multiple of 100
def round_down(x):
return int(math.floor(x / 100.0)) * 100
# Define backtest parameters
initial_capital = 10000
total_capital = [initial_capital] # list with the total capital after every operation
all_profits = [] # list with profits for every operation
ongoing = False
for i in range(0,len(df)):
if ongoing == True:
if ~(np.isnan(df['Sell Price'][i])):
# Define exit point and total profit
exit = df['Sell Price'][i]
profit = shares * (exit - entry)
# Append profit to list and create a new entry with the capital
# after the operation is complete
all_profits += [profit]
current_capital = total_capital[-1] # current capital is the last entry in the list
total_capital += [current_capital + profit]
ongoing = False
else:
if ~(np.isnan(df['Buy Price'][i])):
entry = df['Buy Price'][i]
shares = round_down(initial_capital / entry)
ongoing = TrueEm seguida, vamos analisar qual foi nossa porcentagem de acertos, erros e o lucro total.
def strategy_test(all_profits):
num_operations = len(all_profits)
gains = sum(x >= 0 for x in all_profits)
pct_gains = 100 * (gains / num_operations)
losses = num_operations - gains
pct_losses = 100 - pct_gains
print("Number of operations =", num_operations)
print("Number of gains =", gains, "or", pct_gains.round(), "%")
print("Number of loss =", losses, "or", pct_losses.round(), "%")
print("The total profit was =", sum(all_profits))
strategy_test(all_profits)Number of operations = 160
Number of gains = 117 or 73.0 %
Number of loss = 43 or 27.0 %
The total profit was = 13853.839778900146
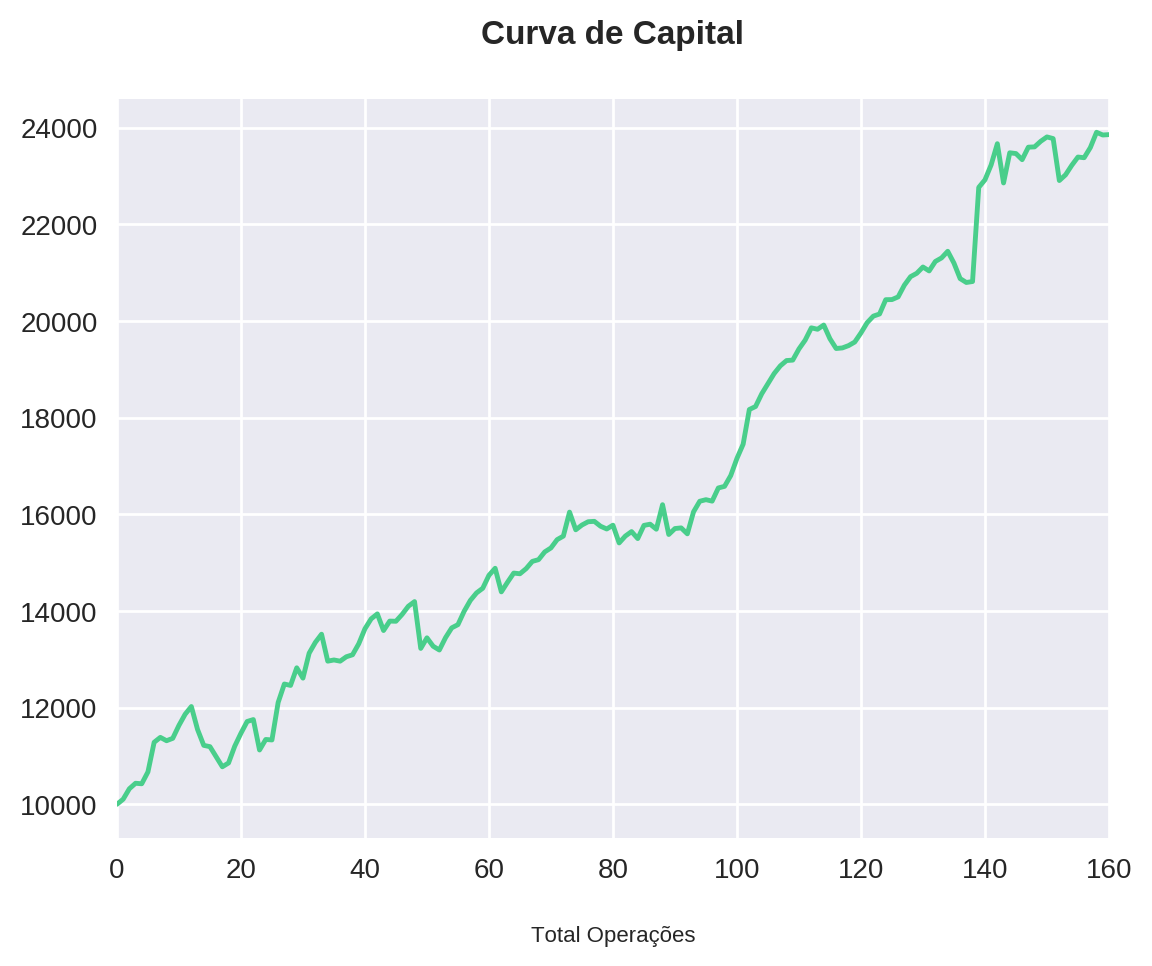
Além da estatística, podemos analisar a evolução do nosso capital a partir do gráfico a seguir.
def capital_plot(total_capital, all_profits):
all_profits = [0] + all_profits # make sure both lists are the same size
cap_evolution = pd.DataFrame({'Capital': total_capital, 'Profit': all_profits})
plt.title("Curva de Capital")
plt.xlabel("Total Operações")
cap_evolution['Capital'].plot()
capital_plot(total_capital, all_profits)
Calculando o tempo médio de operação
Traders mais conservadores podem ficar incomodados com estratégias onde não há nenhum tipo de stop loss. Pensando neles, iremos calcular o tempo médio por operação, a fim de estabelecer um ponto de saída baseado no tempo.
O código a seguir calcula o tempo médio que cada operação leva (independente do resultado), assim como o tempo médio das operações que dão lucro e prejuízo.
days_in_operation = 0
gains_total_days = 0
gains_total_operations = 0
losses_total_days = 0
losses_total_operations = 0
ongoing = False
for i in range(0,len(df)):
if ongoing == True:
days_in_operation += 1
if ~(np.isnan(df['Sell Price'][i])):
exit = df['Sell Price'][i]
is_positive = exit > entry
ongoing = False
# If profit is positive we increment the gains' variables
# Else, we increment the losses' variables
if is_positive > 0:
gains_total_days += days_in_operation
gains_total_operations += 1
else:
losses_total_days += days_in_operation
losses_total_operations += 1
else:
if ~(np.isnan(df['Buy Price'][i])):
entry = df['Buy Price'][i]
ongoing = True
# Operation has started, initialize count of days until it ends
days_in_operation = 0
# Define total number of days and the total number of operations during the period
total_days = gains_total_days + losses_total_days
total_operations = gains_total_operations + losses_total_operations
print("Average length of operations (in days)", total_days / total_operations)
print("Average length of gains (in days)", gains_total_days / gains_total_operations)
print("Average length of losses (in days)", losses_total_days / losses_total_operations)Average length of operations (in days) 3.75
Average length of gains (in days) 2.9145299145299144
Average length of losses (in days) 6.023255813953488
Como podemos observar, as operações que dão lucro levam cerca de 3 dias para ocorrer, enquanto que aquelas que dão prejuízo levam em média o dobro do tempo. Dessa forma, vamos estabelecer um limite de 3 dias para nos proteger de operações muito longas.
Adicionando um stop no tempo
Nosso algoritmo final combina o que foi apresentado até aqui e apresenta uma condição a mais: estabelecemos o ponto de saída no preço de fechamento do dia, caso estejamos no terceiro dia de operação (days_in_operation == max_days).
# Define backtest parameters
initial_capital = 10000
max_days = 3 # add stop in time
# Control variables
total_capital = [initial_capital] # list with the total capital after every operation
all_profits = [] # list with profits for every operation
days_in_operation = 0
gains_total_days = 0
gains_total_operations = 0
losses_total_days = 0
losses_total_operations = 0
ongoing = False
for i in range(0,len(df)):
if ongoing == True:
days_in_operation += 1
# If any of the following conditions are met, the operation will end
if days_in_operation == max_days or ~(np.isnan(df['Sell Price'][i])):
# Define exit point and total profit
exit = np.where(
~(np.isnan(df['Sell Price'][i])),
df['Sell Price'][i],
df['Close'][i])
profit = shares * (exit - entry)
# Append profit to list and create a new entry with the capital
# after the operation is complete
all_profits += [profit]
current_capital = total_capital[-1]
total_capital += [current_capital + profit]
# If profit is positive we increment the gains' variables
# Else, we increment the losses' variables
if profit > 0:
gains_total_days += days_in_operation
gains_total_operations += 1
else:
losses_total_days += days_in_operation
losses_total_operations += 1
ongoing = False
else:
if ~(np.isnan(df['Buy Price'][i])):
entry = df['Buy Price'][i]
shares = round_down(initial_capital / entry)
days_in_operation = 0
ongoing = True
# Define total number of days and the total number of operations during the period
total_days = gains_total_days + losses_total_days
total_operations = gains_total_operations + losses_total_operations
print("Average length of operations (in days)", total_days / total_operations)
print("Average length of gains (in days)", gains_total_days / gains_total_operations)
print("Average length of losses (in days)", losses_total_days / losses_total_operations)Average length of operations (in days) 2.5412371134020617
Average length of gains (in days) 2.2644628099173554
Average length of losses (in days) 3.0
Por fim, iremos calcular novamente as estatísticas da estratégia e analisar a evolução do nosso capital com um stop no tempo.
strategy_test(all_profits)
capital_plot(total_capital, all_profits)Number of operations = 194
Number of gains = 121 or 62.0 %
Number of loss = 73 or 38.0 %
The total profit was = 11720.643138885498
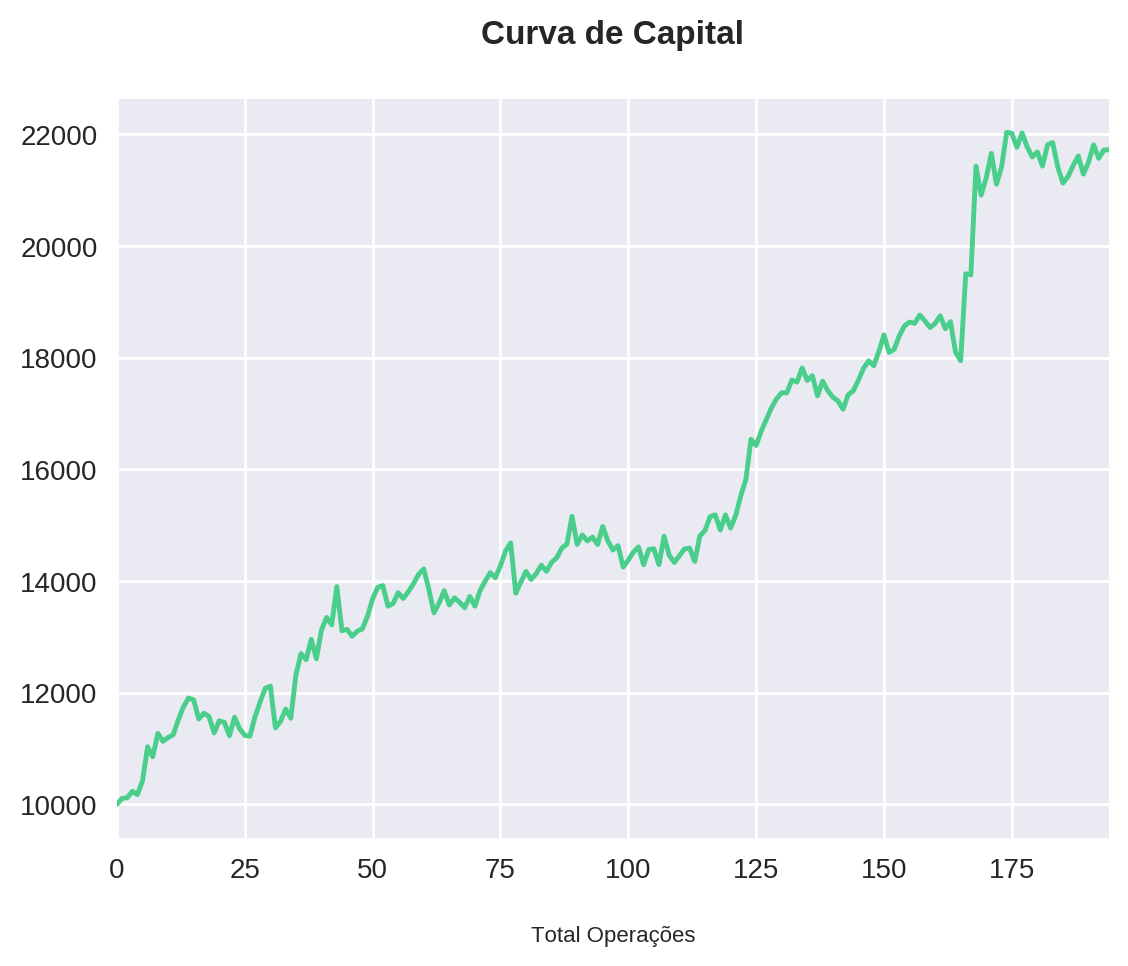
Como esperado, nossa taxa de acerto diminui quando estabelecemos um stop no tempo, uma vez que não estamos deixando o trade se desenrolar. Em contrapartida, espera-se que o drawdown também seja menor. Faremos uma análise mais aprofundada do drawdown em um próximo post, mas já escrevemos sobre como calculá-lo em Entenda o Drawdown e Calcule essa Medida de Volatilidade para Qualquer Ativo.
Nos próximos artigos dessa série sobre o IFR, abordaremos os seguintes tópicos:
- Backtest para outros valores de IFR2, como 10 e 5, e cálculo do drawdown;
- Backtest para outros valores de stop no tempo e outros tipos de stop (por exemplo, quando o IFR chegar acima de um determinado nível);
- Backtest de filtros através da análise de diferentes médias móveis. Muda alguma coisa?
- Backtest da estratégia final em diferentes ativos e intervalos de tempo, a fim de estabelecer uma boa lista de ativos para operar.
Tem muita informação relevante vindo aí para você que busca um melhor desempenho nessa estratégia, então aproveita e se inscreva na nossa newsletter abaixo para não perder nenhum post!
Inscreva-se no canal do QuantBrasil!
Acompanhe novidades sobre a plataforma, vídeos sobre finanças quantitativas, tutoriais sobre programação e Inteligência Artificial!