Analisando Diferentes Parâmetros de Entrada para a Estratégia de IFR2
No âmbito da análise técnica, uma mesma estratégia pode apresentar resultados superiores ao se modificar um simples parâmetro. Por isso se faz tão necessário a realização de backtests, a fim de se alcançar o melhor modelo possível.
No último artigo da série nós testamos a estratégia de IFR2, na qual opera-se na ponta da compra quando o indicador está abaixo ou igual a 30, e vende-se na máxima dos dois dias anteriores. Dando continuidade a esse backtest, iremos analisar possíveis pontos de entrada ao se testar diferentes valores de IFR2 (30, 20, 10 e 5).
Esse artigo envolverá 5 passos:
- Calcular o IFR para 2 períodos;
- Criar uma função para definir os pontos de entrada e saída;
- Criar uma função para o algoritmo que simula as operações;
- Calcular o drawdown e a estatística (taxa de acerto/erro, lucro, entre outros);
- Realizar o backtest para todos os valores de IFR2.
Para isso, utilizaremos diversas funções que já foram desenvolvidas em posts anteriores. Logo, para garantir que você irá acompanhar cada código escrito aqui, vamos recapitular alguns deles:
- Criando o Backtest da Estratégia de IFR2 em Python
- Entenda o Drawdown e Calcule essa Medida de Volatilidade para Qualquer Ativo
Agora que você já revisou todos os códigos, vamos começar!
1. Calcular o IFR para 2 períodos
Antes de qualquer coisa, vamos importar as bibliotecas de interesse e baixar os dados necessários (preço de abertura, máxima, fechamento e fechamento ajustado) de um ativo qualquer nos últimos cinco anos.
# %%capture means we suppress the output
%%capture
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
!pip install yfinance
import yfinance as yfdf = yf.download("LREN3.SA", start="2015-01-01", end="2020-12-30").copy()[["Open", "High", "Close", "Adj Close"]]
df.head()[*********************100%***********************] 1 of 1 completed
| Open | High | Close | Adj Close | |
|---|---|---|---|---|
| Date | ||||
| 2015-01-02 | 12.4975 | 12.5752 | 12.5455 | 10.508009 |
| 2015-01-05 | 12.4678 | 12.4678 | 12.1967 | 10.215857 |
| 2015-01-06 | 12.1488 | 12.4579 | 12.3372 | 10.333539 |
| 2015-01-07 | 12.3769 | 12.6612 | 12.5471 | 10.509348 |
| 2015-01-08 | 12.4959 | 12.6446 | 12.5620 | 10.521830 |
Para o cálculo do IFR2 utilizaremos a mesma função simplificada que criamos no último post dessa série e, igualmente, iremos atribuir o indicador calculado a uma nova coluna do nosso dataframe.
def rsi(data, column, window=2):
data = data.copy()
# Establish gains and losses for each day
data["Variation"] = data[column].diff()
data = data[1:]
data["Gain"] = np.where(data["Variation"] > 0, data["Variation"], 0)
data["Loss"] = np.where(data["Variation"] < 0, data["Variation"], 0)
# Calculate simple averages so we can initialize the classic averages
simple_avg_gain = data["Gain"].rolling(window).mean()
simple_avg_loss = data["Loss"].abs().rolling(window).mean()
classic_avg_gain = simple_avg_gain.copy()
classic_avg_loss = simple_avg_loss.copy()
for i in range(window, len(classic_avg_gain)):
classic_avg_gain[i] = (classic_avg_gain[i - 1] * (window - 1) + data["Gain"].iloc[i]) / window
classic_avg_loss[i] = (classic_avg_loss[i - 1] * (window - 1) + data["Loss"].abs().iloc[i]) / window
# Calculate the RSI
RS = classic_avg_gain / classic_avg_loss
RSI = 100 - (100 / (1 + RS))
return RSIdf["IFR2"] = rsi(df, column="Adj Close")
df.head()| Open | High | Close | Adj Close | IFR2 | |
|---|---|---|---|---|---|
| Date | |||||
| 2015-01-02 | 12.4975 | 12.5752 | 12.5455 | 10.508009 | NaN |
| 2015-01-05 | 12.4678 | 12.4678 | 12.1967 | 10.215857 | NaN |
| 2015-01-06 | 12.1488 | 12.4579 | 12.3372 | 10.333539 | 28.714604 |
| 2015-01-07 | 12.3769 | 12.6612 | 12.5471 | 10.509348 | 61.632231 |
| 2015-01-08 | 12.4959 | 12.6446 | 12.5620 | 10.521830 | 63.993122 |
2. Criar uma função para definir os pontos de entrada e saída
Com o IFR2 calculado, daqui em diante nós criaremos funções para cada passo, a fim de utilizá-las mais para frente para iterar sobre nossa lista de parâmetros (30, 20, 10 e 5). Portanto, o segundo passo é criar uma função que irá definir os pontos de entrada e saída da nossa estratégia.
A função strategy_points irá aceitar dois argumentos: o dataframe e o valor do parâmetro de IFR2, respectivamente. O código, por sua vez, abrange não só a criação das colunas para isolar os possíveis pontos de entrada e saída, como também envolve a lógica para estabelecer os exatos preços de compra e venda, retornando enfim, o nosso dataframe com todas as informações necessárias.
def strategy_points(data, rsi_parameter):
data["Target1"] = data["High"].shift(1)
data["Target2"] = data["High"].shift(2)
data["Target"] = data[["Target1", "Target2"]].max(axis=1)
# We don't need them anymore
data.drop(columns=["Target1", "Target2"], inplace=True)
# Define exact buy price
data["Buy Price"] = np.where(data["IFR2"] <= rsi_parameter, data["Close"], np.nan)
# Define exact sell price
data["Sell Price"] = np.where(
data["High"] > data['Target'],
np.where(data['Open'] > data['Target'], data['Open'], data['Target']),
np.nan)
return data 3. Criar uma função para o algoritmo que simula as operações
De maneira semelhante, criaremos uma função para o algoritmo em cima do código desenvolvido anteriormente.
Esta função (backtest_algorithm) também aceitará dois argumentos: o dataframe e o montante de capital alocado para a estratégia (initial_capital), que terá como padrão R$ 10.000. Além disso, a função retornará duas listas, uma com o lucro de cada operação (all_profits) e outra com o capital acumulado após cada operação (total_capital).
import math
# Create a function to round any number to the smallest multiple of 100
def round_down(x):
return int(math.floor(x / 100.0)) * 100
def backtest_algorithm(data, initial_capital=10000):
# List with the total capital after every operation
total_capital = [initial_capital]
# List with profits for every operation. We initialize with 0 so
# both lists have the same size
all_profits = [0]
ongoing = False
for i in range(0,len(data)):
if ongoing == True:
if ~(np.isnan(data['Sell Price'][i])):
# Define exit point and total profit
exit = data['Sell Price'][i]
profit = shares * (exit - entry)
# Append profit to list and create a new entry with the capital
# after the operation is complete
all_profits += [profit]
current_capital = total_capital[-1] # current capital is the last entry in the list
total_capital += [current_capital + profit]
ongoing = False
else:
if ~(np.isnan(data['Buy Price'][i])):
entry = data['Buy Price'][i]
shares = round_down(initial_capital / entry)
ongoing = True
return all_profits, total_capital4. Calcular o drawdown e a estatística
O próximo passo é praticamente Ctrl+C e Ctrl+V!
O post sobre drawdown nos dá a função pronta (get_drawdown). Esta recebe dois argumentos: o dataframe e a coluna com os valores nos quais se deseja saber o drawdown.
def get_drawdown(data, column = "Adj Close"):
data["Max"] = data[column].cummax()
data["Delta"] = data['Max'] - data[column]
data["Drawdown"] = 100 * (data["Delta"] / data["Max"])
max_drawdown = data["Drawdown"].max()
return max_drawdownComo o drawdown é uma medida importante na hora de se avaliar uma estratégia, nós o incluiremos na nossa função final, junto com todos os outros resultados (taxa de acerto/erro, lucro, entre outros). Dessa forma, iremos fazer algumas modificações no código da função strategy_test.
A parte inicial da função será a mesma: calculará o número total de operações (num_operation), o número de operações que deram lucro/prejuízo (gains e losses), suas respectivas porcentagens (pct_gains e pct_losses), e o lucro total (total_profit). Iremos incluir também o cálculo do lucro, em porcentagem, em relação ao nosso capital inicial (pct_profit).
Em seguida, transformaremos a lista de capital acumulado (total_capital) em um dataframe para então ser utilizado em get_drawdown. Por fim, retornaremos um dicionário com todos os resultados calculados.
def strategy_test(all_profits, total_capital):
num_operations = (len(all_profits) - 1)
gains = sum(x >= 0 for x in all_profits)
pct_gains = 100 * (gains / num_operations)
losses = num_operations - gains
pct_losses = 100 - pct_gains
total_profit = sum(all_profits)
# The first value entry in total_capital is the initial capital
pct_profit = (total_profit / total_capital[0]) * 100
# Compute drawdown
total_capital = pd.DataFrame(data=total_capital, columns=["total_capital"])
drawdown = get_drawdown(data=total_capital, column="total_capital")
return {
"num_operations": num_operations,
"gains": gains ,
"pct_gains": pct_gains.round(),
"losses": losses,
"pct_losses": pct_losses.round(),
"total_profit": total_profit,
"pct_profit": pct_profit,
"drawdown": drawdown
}5. Realizar o backtest
Finalmente, o último passo é realizar o backtest. Faremos isso através de um loop, no qual iremos iterar sobre nossa lista de parâmetros (parameters) e rodar cada função criada nos passos anteriores.
Armazenaremos as informações provenientes do loop em dois dicionários diferentes: um com toda a estatística das 4 estratégias (statistics) e outro com o lucro e capital acumulado de cada operação (cap_evolution). Isso nos facilitará na hora de avaliar cada uma delas, uma vez que seremos capazes de plotá-las em gráficos, melhorando assim a visualização dos dados.
parameters = [30, 20, 10, 5]
statistics = {}
cap_evolution = {}
for parameter in parameters:
df = strategy_points(data=df, rsi_parameter=parameter)
all_profits, total_capital = backtest_algorithm(df)
statistics[parameter] = strategy_test(all_profits, total_capital)
key1 = "all_profits_" + str(parameter)
key2 = "total_capital_" + str(parameter)
cap_evolution[parameter] = { key1: all_profits, key2: total_capital }
Vamos dar uma olhada no dicionário com os resultados da estatística. Todas as informações para avaliarmos nossa estratégia estão nele, mas a visualização ainda não é das melhores.
statistics{30: {'num_operations': 160, 'gains': 118, 'pct_gains': 74.0, 'losses': 42, 'pct_losses': 26.0, 'total_profit': 13853.839778900146, 'pct_profit': 138.53839778900146, 'drawdown': 10.36921769407645}, 20: {'num_operations': 128, 'gains': 100, 'pct_gains': 78.0, 'losses': 28, 'pct_losses': 22.0, 'total_profit': 13481.931686401367, 'pct_profit': 134.81931686401367, 'drawdown': 7.1133064485273305}, 10: {'num_operations': 73, 'gains': 56, 'pct_gains': 77.0, 'losses': 17, 'pct_losses': 23.0, 'total_profit': 8771.174621582031, 'pct_profit': 87.71174621582031, 'drawdown': 5.175766110091191}, 5: {'num_operations': 36, 'gains': 29, 'pct_gains': 81.0, 'losses': 7, 'pct_losses': 19.0, 'total_profit': 5809.770774841309, 'pct_profit': 58.097707748413086, 'drawdown': 5.346493917637023}}O pandas possui uma função que nos permite transformar um dicionário diretamente em um dataframe: pd.DataFrame.from_dict(). Esta recebe o dicionário como argumento e nos permite escolher a orientação em relação às chaves do dicionário. Usaremos orient='index' para determinar que as chaves irão corresponder às linhas.
statistics_df = pd.DataFrame.from_dict(statistics, orient='index')
statistics_df
| num_operations | gains | pct_gains | losses | pct_losses | total_profit | pct_profit | drawdown | |
|---|---|---|---|---|---|---|---|---|
| 30 | 160 | 118 | 74.0 | 42 | 26.0 | 13853.839779 | 138.538398 | 10.369218 |
| 20 | 128 | 100 | 78.0 | 28 | 22.0 | 13481.931686 | 134.819317 | 7.113306 |
| 10 | 73 | 56 | 77.0 | 17 | 23.0 | 8771.174622 | 87.711746 | 5.175766 |
| 5 | 36 | 29 | 81.0 | 7 | 19.0 | 5809.770775 | 58.097708 | 5.346494 |
Repare que as duas últimas colunas apresentam muitas casas decimais que acabam poluindo o nosso dataframe. Vamos arrendondar esses números através da função .round() e restringi-los a apenas 2 casas decimais.
statistics_df = statistics_df.round(2)
statistics_df
| num_operations | gains | pct_gains | losses | pct_losses | total_profit | pct_profit | drawdown | |
|---|---|---|---|---|---|---|---|---|
| 30 | 160 | 118 | 74.0 | 42 | 26.0 | 13853.84 | 138.54 | 10.37 |
| 20 | 128 | 100 | 78.0 | 28 | 22.0 | 13481.93 | 134.82 | 7.11 |
| 10 | 73 | 56 | 77.0 | 17 | 23.0 | 8771.17 | 87.71 | 5.18 |
| 5 | 36 | 29 | 81.0 | 7 | 19.0 | 5809.77 | 58.10 | 5.35 |
A visualização ficou melhor que no formato de dicionário, certo? Pois iremos melhorar ainda mais! Vamos agora plotar as informações mais relevantes (número de operações, % de acerto e o lucro total) em gráficos de barra.
Para isso, criaremos um função a fim de plotar um gráfico de barras para cada um desses resultados. A função plot_bars receberá como argumentos, na ordem:
- o título do gráfico;
- o valor do eixo x;
- o valor do eixo y;
- a legenda do eixo x, que será "IFR2" por padrão;
- a legenda do eixo y, que será opcional.
def plot_bars(title, x, y, x_label="IFR2", y_label=None):
fig = plt.figure()
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['top'].set_visible(False)
colors = ["paleturquoise", "mediumturquoise", "darkcyan", "darkslategrey"]
plt.bar(x, y, color=colors)
plt.title(title)
plt.xlabel(x_label)
if y_label != None:
plt.ylabel(y_label)
for i, v in enumerate(y):
plt.text(
x=i,
y=v,
s=str(v),
horizontalalignment='center',
verticalalignment='bottom'
)Para o eixo x, utilizaremos o índice do dataframe em formato de string. Isso é necessário para que tenhamos o valor exato de cada parâmetro para cada barra, e não um range de 30 a 5.
x = statistics_df.index.astype(str)Agora vamos plotar os gráficos!
plot_bars(title="Número de Operações", x=x, y=statistics_df["num_operations"])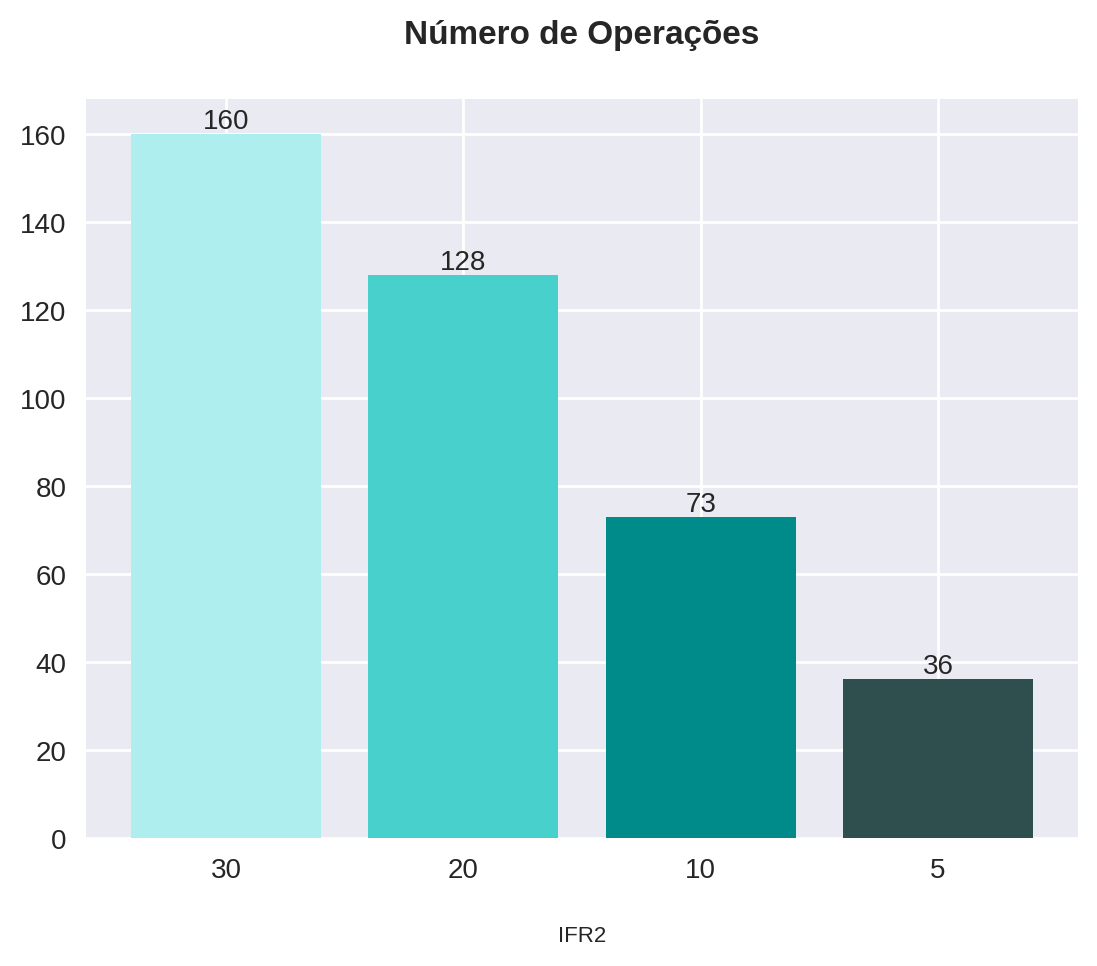
plot_bars(title="Taxa de Acerto (%)", x=x, y=statistics_df["pct_gains"])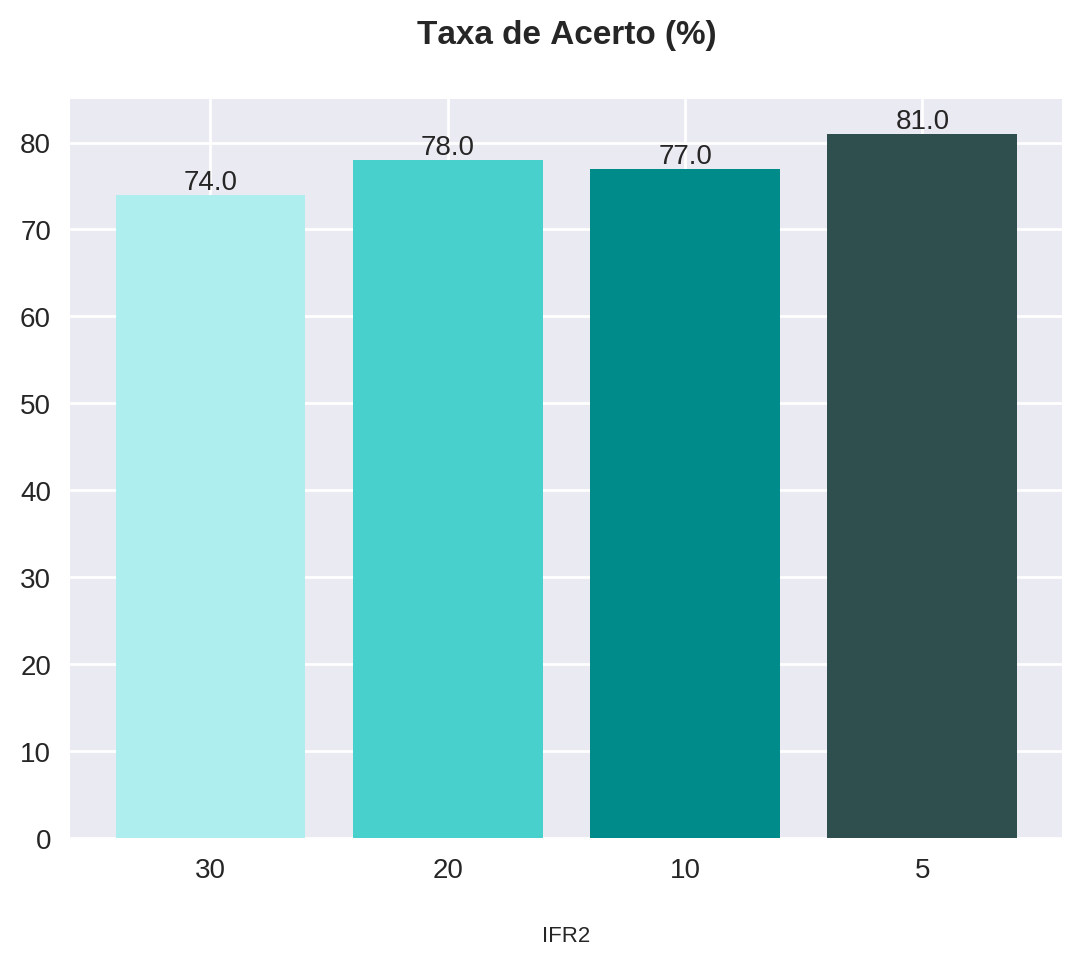
plot_bars(title="Lucro Total (%)", x=x, y=statistics_df["pct_profit"])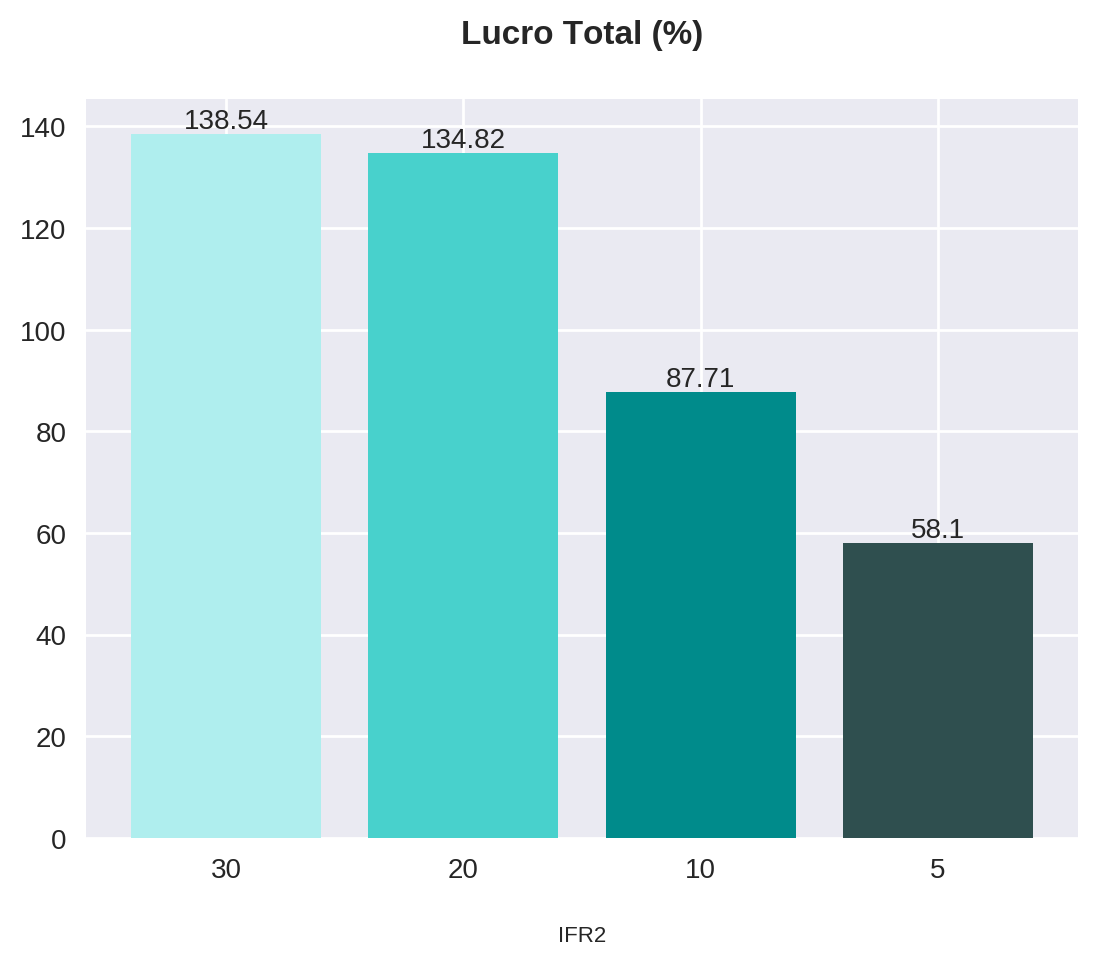
plot_bars(title="Drawdown (%)", x=x, y=statistics_df["drawdown"])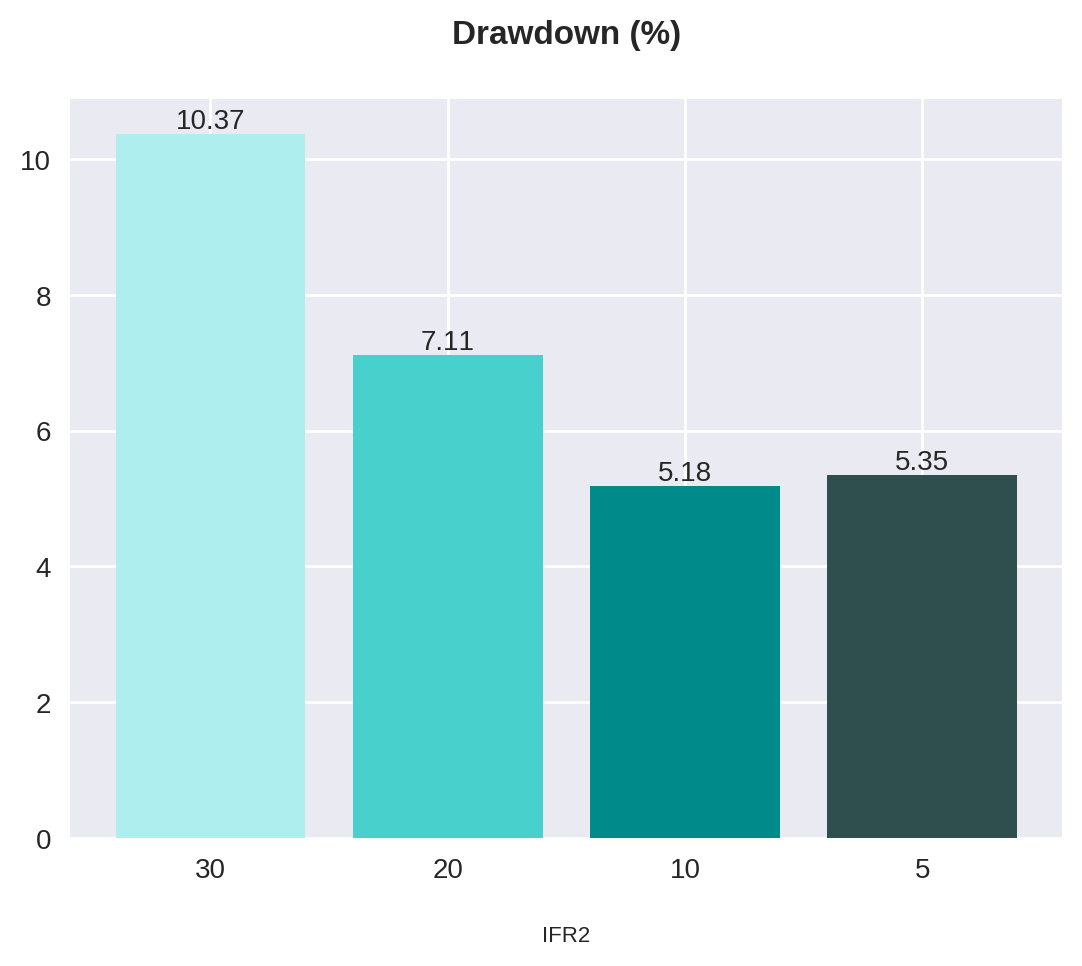
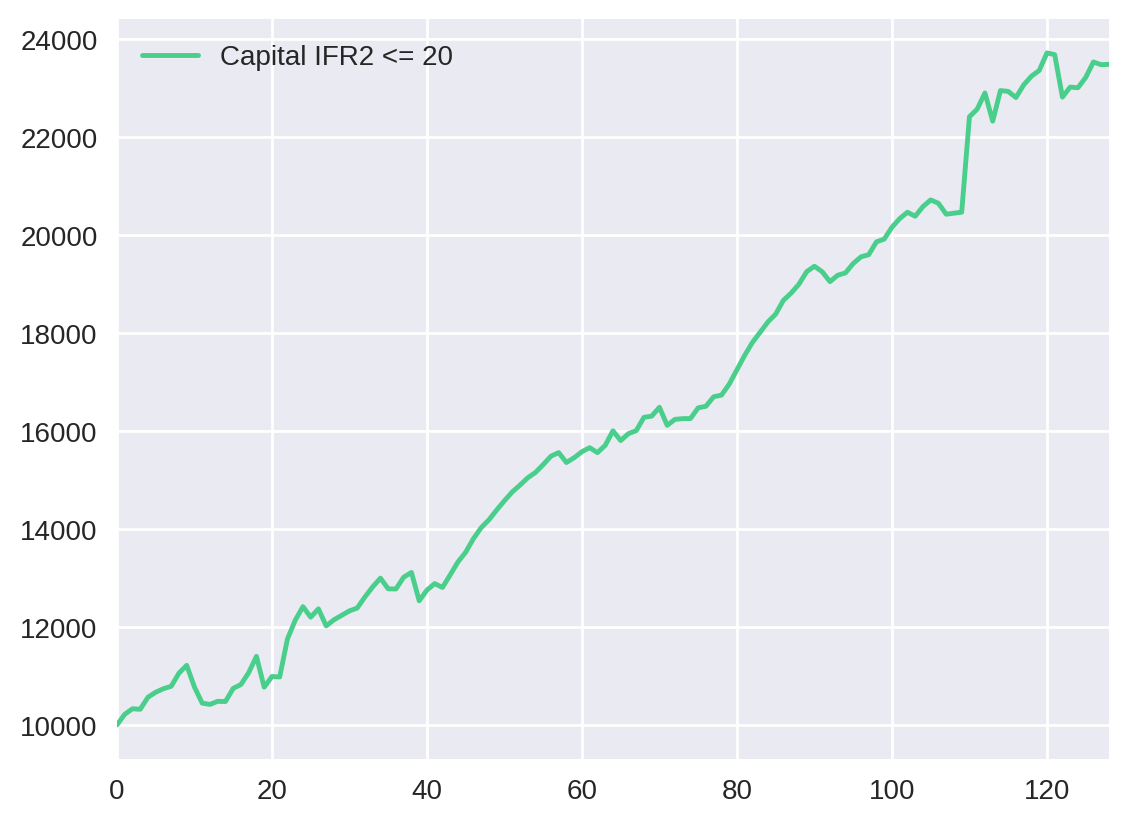
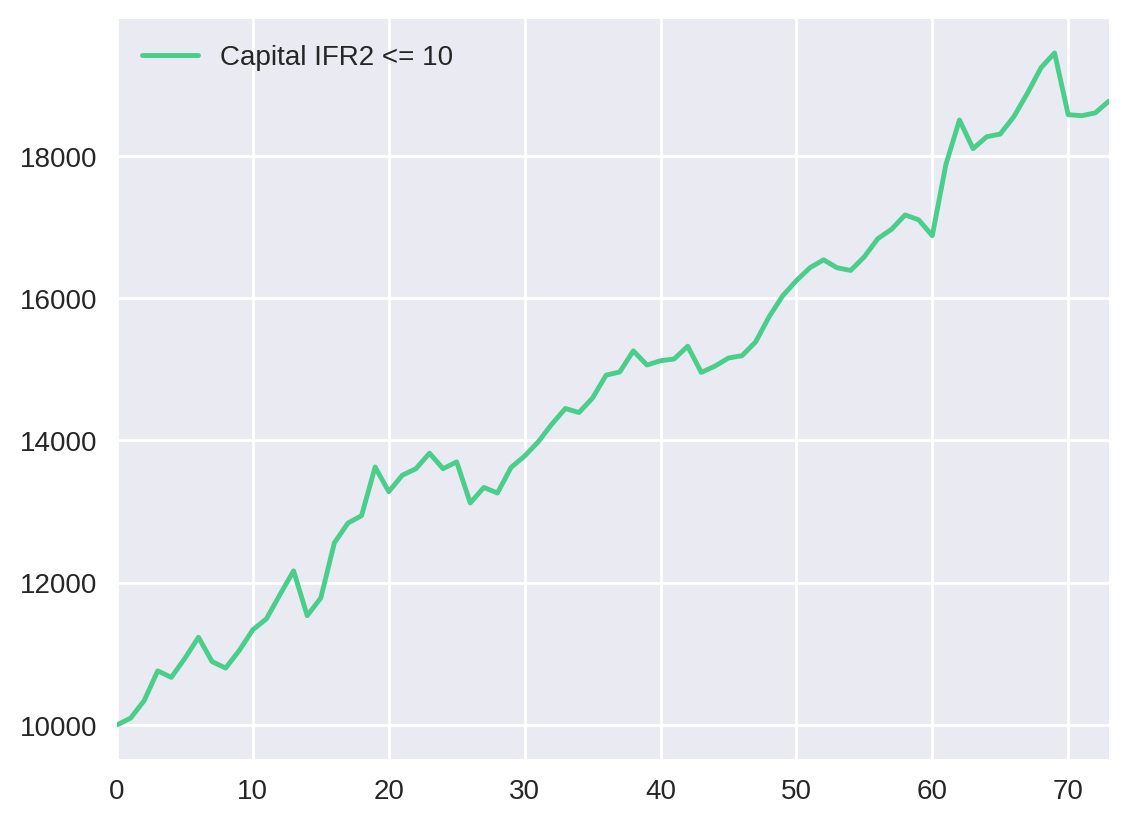
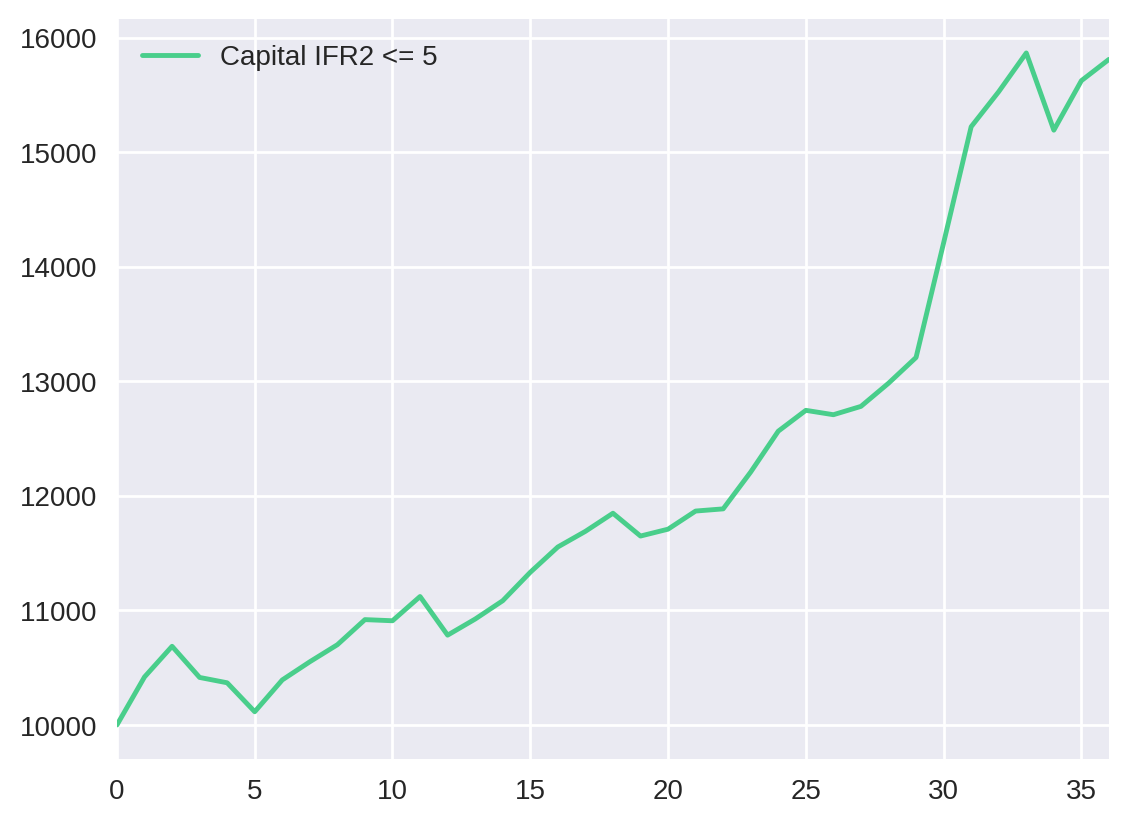
Podemos embasar ainda mais nossa análise ao visualizar a evolução do capital em cada uma dessas estratégias. Portanto, plotaremos o total_capital para cada parâmetro:
pd.DataFrame({"Capital IFR2 <= 30": cap_evolution[30]["total_capital_30"]}).plot()
pd.DataFrame({"Capital IFR2 <= 20": cap_evolution[20]["total_capital_20"]}).plot()
pd.DataFrame({"Capital IFR2 <= 10": cap_evolution[10]["total_capital_10"]}).plot()
pd.DataFrame({"Capital IFR2 <= 5": cap_evolution[5]["total_capital_5"]}).plot()<matplotlib.axes._subplots.AxesSubplot at 0x7f52401aed50>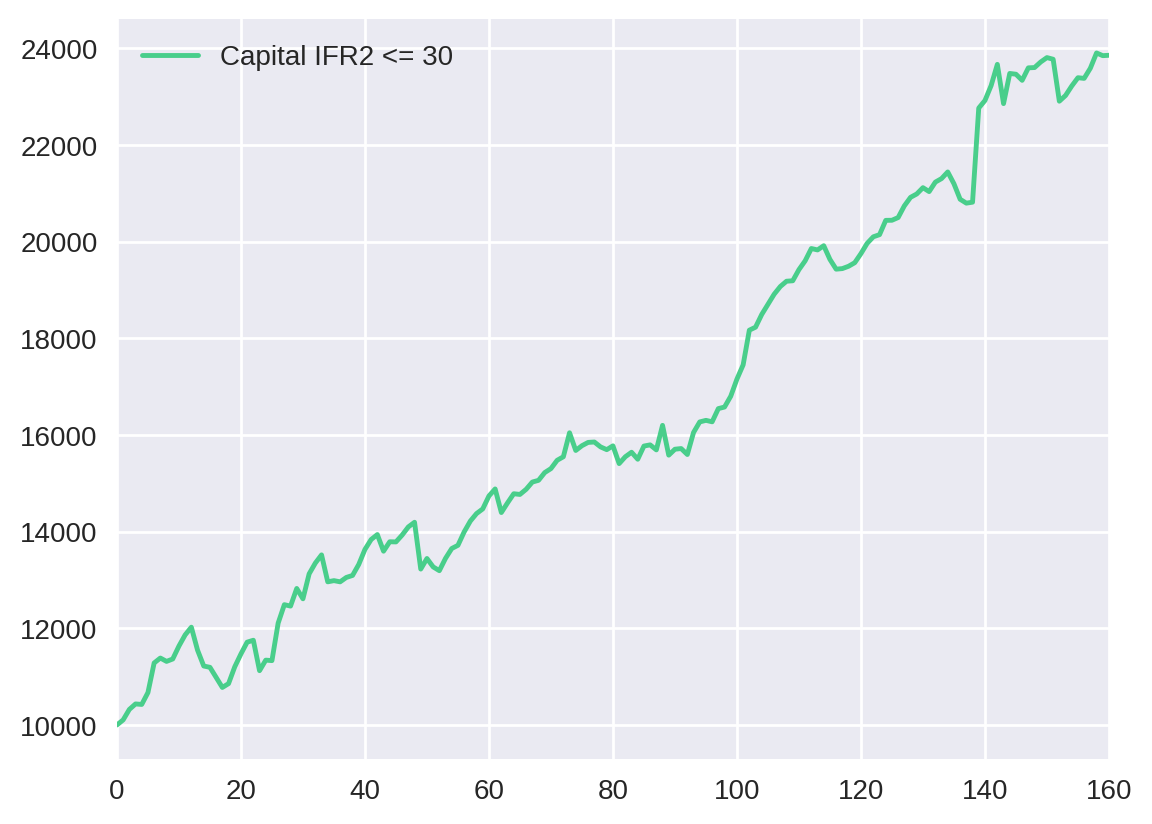
Conclusão
Apesar de não termos feito nenhum teste de significância, podemos considerar que as estratégias utilizando valores de IFR2 de 30 e 20 tiveram resultados semelhantes, assim como o par 10 e 5. Observe pela tabela abaixo.
| IFR2 <= | Lucro (%) | Drawdown máx. (%) |
|---|---|---|
| 30 | 138.54 | 10.37 |
| 20 | 134.82 | 7.11 |
| 10 | 87.71 | 5.18 |
| 5 | 58.10 | 5.35 |
Resumindo, a estratégia com parâmetro de 30 possui o melhor lucro (138%), mas apresenta o maior drawdown (10.4%). Por outro lado, a estratégia com parâmetro de 5 tem um dos menores drawdowns (5.3%), embora apresente o menor lucro de todos (58%). Esse resultado representa uma das regras básicas do mercado financeiro: quanto maior o risco, maior o potencial de ganho. Dessa forma, a relação lucro/drawdown adequada é questão de estratégia e perfil de cada investidor.
Além disso, nesse backtest não estamos levando em consideração um fator relevante: o ativo. Para um ativo em forte tendência de alta, dificilmente o IFR2 irá atingir valores muito inferiores, como 5. Analogamente, em uma forte tendência de baixa, é possível que valores menores de IFR2 funcionem melhor.
Nos próximos posts, analisaremos os seguintes aspectos:
- Backtest do IFR2 para ativos em diferentes tendências;
- Estatísticas para diferentes estratégias de stop loss;
- Resultados utilizando filtros de seleção, como médias móveis.
Inscreva-se no canal do QuantBrasil!
Acompanhe novidades sobre a plataforma, vídeos sobre finanças quantitativas, tutoriais sobre programação e Inteligência Artificial!