Como Identificar Linhas de Suporte e Resistência Utilizando Python
No artigo de hoje aprederemos a traçar linhas de suporte e resistência em um gráfico de candlestick (ou gráfico de vela, em português) utilizando somente Python e Matplotlib.
Antes de partirmos para o código, vamos entender um pouco sobre esses termos da análise técnica.
O que são linhas de Suporte e Resistência?
Linhas de suporte e resistência representam pontos gráficos em que o preço geralmente não ultrapassa um determinado patamar. Uma linha de suporte por exemplo, caracteriza um fundo, onde a pressão compradora demonstrou-se maior que a pressão vendedora em algum (ou vários) momento no passado. Por outro lado, uma linha de resistência caracteriza um topo, onde a pressão vendedora foi maior que a compradora.
De uma maneira geral, topos e fundos do passado tendem a continuar funcionando no futuro, se consolidando portanto, como zonas de suporte e resistência. Dessa forma, em uma tendência de alta, os fundos costumam segurar as correções de preço (configurando um bom ponto de compra), ao passo que topos são defendidos por vendedores em uma tendência de baixa (configurando assim, um bom ponto de venda).
Dito isso, saber reconhecer essas zonas é essencial na hora de analisar o comportamento de um ativo ao longo do tempo e para reconhecê-los, utilizaremos os padrões fractais.
Entendendo o padrão Fractal
Fractal nada mais é do que um padrão estabelecido por pelo menos 5 candles, onde o candle central (candle de sinal) apresenta máxima ou mínima maior do que os dois candles ao seu extremo.
Dessa forma, para estabelecer uma linha de resistência, o candle de sinal deve apresentar o maior valor de máxima, acompanhado por valores crescentes de máxima dos dois candles anterioes e valores decrescentes dos dois candles posteriores. A mesma ideia se aplica para estabelecer uma linha de Suporte. Veja pela figura abaixo.
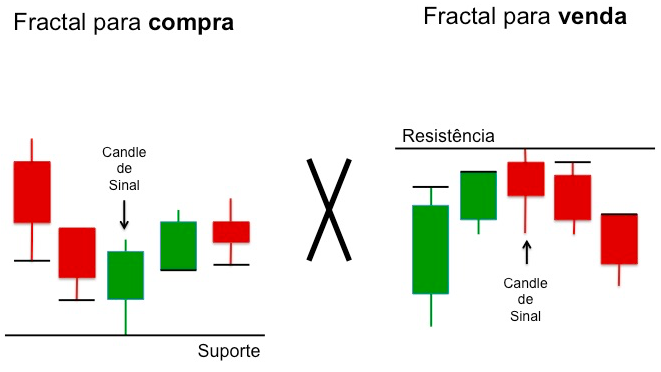
Bem simples, certo?! Entendido isso, podemos colocar a mão na massa!
O código a seguir foi baseado no artigo do cientista de dados Gianluca Malato para o Towards Data Science, com algumas alterações e atualizações.
Importando as bibliotecas e baixando os dados necessárias
Utilizaremos somente duas bibliotecas: Yahoo Finance, para baixar os preços de um ativo qualquer, e Matplotlib Finance, um módulo Matplotlib para visualização e análise de dados financeiros.
!pip install -q yfinance
import yfinance as yf
!pip install --upgrade -q mplfinance
import mplfinance as mpfBaixaremos os dados de PETR4 a partir do início do ano até o último pregão antes da publicação desse post.
ticker = 'PETR4.SA'
start = '2021-01-01'
end = '2021-09-15'
df = yf.download(ticker, start, end)
df
[*********************100%***********************] 1 of 1 completed
| Open | High | Low | Close | Adj Close | Volume | |
|---|---|---|---|---|---|---|
| Date | ||||||
| 2021-01-04 | 28.650000 | 29.180000 | 28.530001 | 28.910000 | 26.396519 | 74719700 |
| 2021-01-05 | 28.900000 | 30.180000 | 28.240000 | 30.040001 | 27.428274 | 95181100 |
| 2021-01-06 | 30.160000 | 30.900000 | 30.049999 | 30.100000 | 27.483057 | 96562500 |
| 2021-01-07 | 30.340000 | 31.150000 | 30.340000 | 31.000000 | 28.304810 | 56171300 |
| 2021-01-08 | 31.459999 | 31.760000 | 30.350000 | 31.120001 | 28.414377 | 67136300 |
| ... | ... | ... | ... | ... | ... | ... |
| 2021-09-08 | 26.290001 | 26.350000 | 24.790001 | 24.969999 | 24.969999 | 80378400 |
| 2021-09-09 | 25.080000 | 25.879999 | 24.139999 | 25.500000 | 25.500000 | 156617100 |
| 2021-09-10 | 26.020000 | 26.139999 | 25.330000 | 25.340000 | 25.340000 | 78379900 |
| 2021-09-13 | 25.799999 | 26.389999 | 25.639999 | 26.230000 | 26.230000 | 63317900 |
| 2021-09-14 | 25.950001 | 26.250000 | 25.719999 | 25.879999 | 25.879999 | 65497300 |
173 rows × 6 columns
Criando as funções que identificarão os fractais
Para reconhecer os padrões fractais formados durante o período em questão, escreveremos o código da perspectiva do candle de sinal.
Dessa forma, para identificar uma linha de resistência (is_resistance), o candle de sinal deverá ter máxima maior que o candle anterior (i-1) e porterior (i+1) a ele, assim como ambos deverão apresentar máxima maior que os candles de suas extremidades (i-2 e i+2, respectivamente). A mesma lógica se aplica para is_support.
def is_resistance(df,i):
support = (df['High'][i] > df['High'][i-1]
and df['High'][i] > df['High'][i+1]
and df['High'][i+1] > df['High'][i+2]
and df['High'][i-1] > df['High'][i-2])
return support
def is_support(df,i):
support = (df['Low'][i] < df['Low'][i-1]
and df['Low'][i] < df['Low'][i+1]
and df['Low'][i+1] < df['Low'][i+2]
and df['Low'][i-1] < df['Low'][i-2])
return supportPosicionando as linhas de suporte e resistência
Para traçar as linhas que representarão os pontos de suporte e resistência, utilizaremos o parâmetro alines da função mpf.plot, que nos permite plotar linhas horizontais no gráfico.
O alines recebe um par de tuplas com coordenadas (x, y), onde a primeira tupla representa o ponto de início da linha e a segunda tupla, o ponto final da linha. No nosso caso, o primeiro ponto será o dia onde o suporte ou resistência foi observado, e o último ponto será o último dia do nosso dataset.
# coordinates is a list of a list of two tuples
# the first tuple has the signal candle's index as 1st argument and the price as 2nd
# the second tuple has the last index as 1st argument in order to draw the support/resistance
# line till the end of the graph
coordinates = []
for i in range(2, df.shape[0] - 2):
if is_support(df, i):
coordinates.append([
(df.index[i], df['Low'][i]), # If support, plot a horizontal line from the low
(max(df.index),df['Low'][i])
])
elif is_resistance(df, i):
coordinates.append([
(df.index[i],df['High'][i]), # If resistance, plot a horizontal line from the high
(max(df.index),df['High'][i])
])
coordinates[:5][[(Timestamp('2021-01-20 00:00:00'), 29.1200008392334), (Timestamp('2021-09-14 00:00:00'), 29.1200008392334)], [(Timestamp('2021-02-22 00:00:00'), 21.399999618530273), (Timestamp('2021-09-14 00:00:00'), 21.399999618530273)], [(Timestamp('2021-02-25 00:00:00'), 25.25), (Timestamp('2021-09-14 00:00:00'), 25.25)], [(Timestamp('2021-03-03 00:00:00'), 20.479999542236328), (Timestamp('2021-09-14 00:00:00'), 20.479999542236328)], [(Timestamp('2021-03-05 00:00:00'), 23.219999313354492), (Timestamp('2021-09-14 00:00:00'), 23.219999313354492)]]Com essas informações, podemos escrever uma função para plotarmos o gráfico.
Plotando o gráfico com os suportes e resistências
Como nosso objetivo é plotar um gráfico de candlestick e suas linhas horizontais, teremos que chamar a função mpf.plot mais de uma vez para o mesmo gráfico (ax2 = ax1.twinx()).
A primeira vez que chamaremos a função será para plotar o gráfico de candlestick (type='candle') com o estilo yahoo, onde os candles que fecharam positivo são representados por verde e os que fecharam negativo, por vermelho. Você pode explorar diversos estilos e tipos de gráficos disponíveis na documentação.
Em seguida, iteraremos sobre todas as coordenadas presentes em coordinates, a fim de plotar as linhas horizontas.
def plot_all(coordinates):
fig = mpf.figure(figsize=(16, 10))
title = f"Supports and Resistances: {ticker.replace('.SA', '')}"
ax1 = fig.subplot(title=title)
ax2 = ax1.twinx()
mpf.plot(df,
ax=ax1,
style='yahoo',
type='candle',
ylabel='Price')
for coordinate in coordinates:
mpf.plot(df, alines=(coordinate), ax=ax2)
plot_all(coordinates)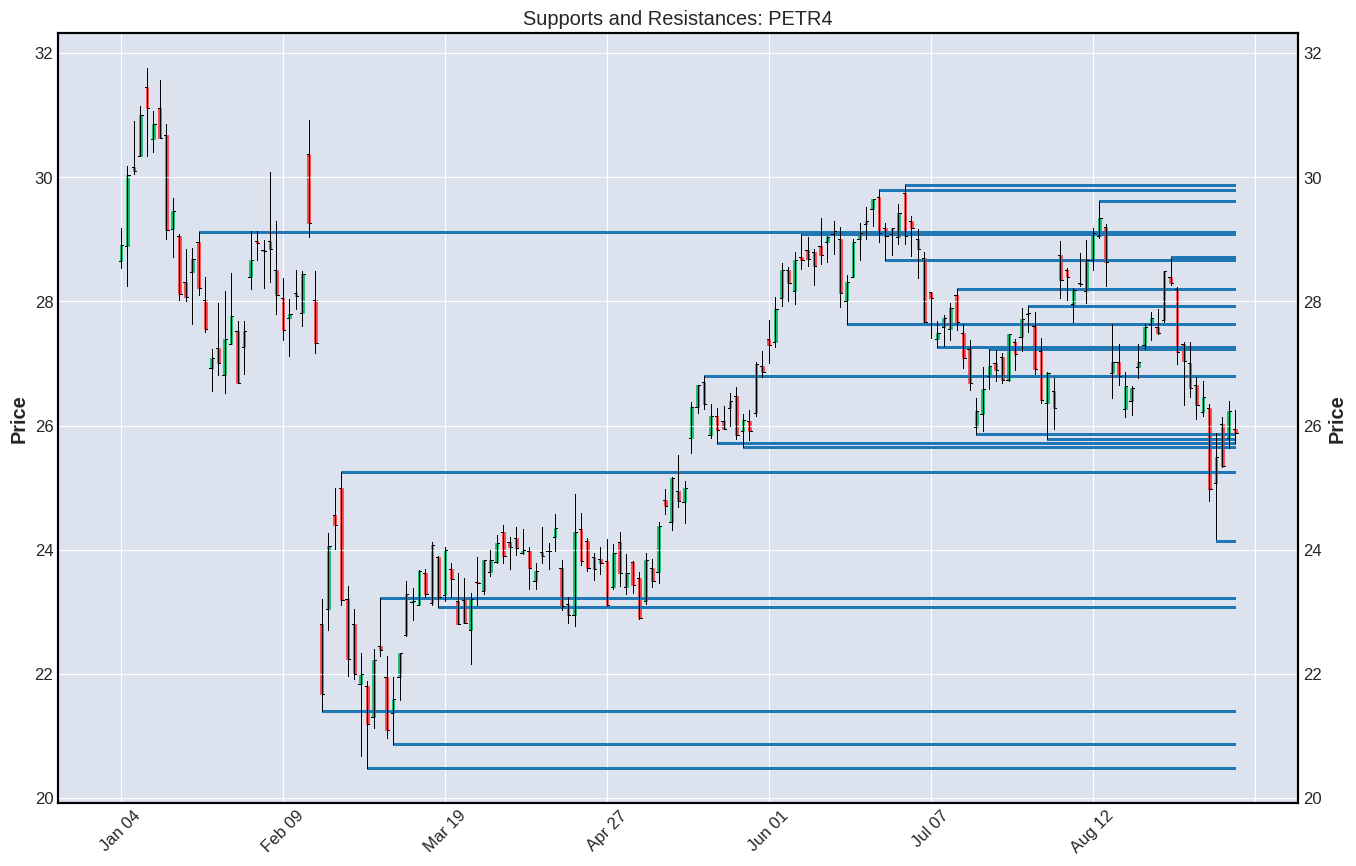
Como podemos perceber, algumas linhas foram traçadas muito próximas uma das outras, o que é desnecessário e confuso, uma vez que estamos interessados em zonas de suporte e resistência.
Para melhorar a visualização do nosso gráfico, vamos criar uma função para excluir essas linhas próximas entre si.
Refinando o nosso gráfico
Existem diversas formas de se calcular o tamanho esperado de um candle (Average True Range ou ATR sendo um deles). Por simplicidade, vamos definir o tamanho médio dos candles, ou seja, a média da diferença entre a máxima e a mínima dos candles.
Dessa maneira, se a diferença entre duas linhas, seja ela de suporte ou resistência, for menor que a média dos corpos dos candles, quer dizer que elas estão muito próximas entre si e pertencem à mesma zona.
import numpy as np
avg_candle_size = np.mean(df['High'] - df['Low'])
avg_candle_size
0.8173410272322639Escreveremos então uma função para comparar a distância entre as linhas: is_far_from_level.
A função a seguir verificará se um dado preço (price) está distante o suficiente de uma lista de suportes e resistências (levels). Para medir a distância, utilizaremos a variável delta, que no nosso caso será o avg_candle_size.
def is_far_from_level(price, levels, delta):
is_far = True
for level in levels:
if (abs(level - price) < delta):
is_far = False
break
return is_farDessa forma, ao iterarmos novamente sobre as funções is_support e is_resistance, isolaremos os preços de suporte e resistência na lista no_noise_levels sempre utilizando a função is_far_from_level para comparar com o preço da próxima linha.
Logo, a função is_far_from_level seguirá a seguinte lógica: se o preço for menor que o avg_candle_size de pelo menos uma linha de suporte ou resistência (level), consideramos que os preços estão próximos e assim ele é descartado. Por outro lado, caso o preço não esteja próximo o suficiente de nenhum suporte ou resistência, esse preço será considerado distante e será adicionado a lista no_noise_levels.
Além disso, adicionaremos as novas coordenadas à uma nova lista coordinates para sermos capazes de plotar as linhas horizontais.
no_noise_levels = []
coordinates = []
# We skip the first and the last 2 data points once we need at least 5 candles
# to form the patter
for i in range(2, df.shape[0] - 2):
if is_support(df, i):
price = df['Low'][i]
if is_far_from_level(price, no_noise_levels, avg_candle_size):
no_noise_levels.append(price)
coordinates.append([
(df.index[i], price), (max(df.index), price)
])
elif is_resistance(df,i):
price = df['High'][i]
if is_far_from_level(price, no_noise_levels, avg_candle_size):
no_noise_levels.append(price)
coordinates.append([
(df.index[i], price), (max(df.index), price)
])
coordinates
[[(Timestamp('2021-01-20 00:00:00'), 29.1200008392334), (Timestamp('2021-09-14 00:00:00'), 29.1200008392334)], [(Timestamp('2021-02-22 00:00:00'), 21.399999618530273), (Timestamp('2021-09-14 00:00:00'), 21.399999618530273)], [(Timestamp('2021-02-25 00:00:00'), 25.25), (Timestamp('2021-09-14 00:00:00'), 25.25)], [(Timestamp('2021-03-03 00:00:00'), 20.479999542236328), (Timestamp('2021-09-14 00:00:00'), 20.479999542236328)], [(Timestamp('2021-03-05 00:00:00'), 23.219999313354492), (Timestamp('2021-09-14 00:00:00'), 23.219999313354492)], [(Timestamp('2021-05-18 00:00:00'), 26.799999237060547), (Timestamp('2021-09-14 00:00:00'), 26.799999237060547)], [(Timestamp('2021-06-18 00:00:00'), 27.639999389648438), (Timestamp('2021-09-14 00:00:00'), 27.639999389648438)], [(Timestamp('2021-09-09 00:00:00'), 24.139999389648438), (Timestamp('2021-09-14 00:00:00'), 24.139999389648438)]]Por fim, basta plotarmos a função do gráfico novamente.
plot_all(coordinates)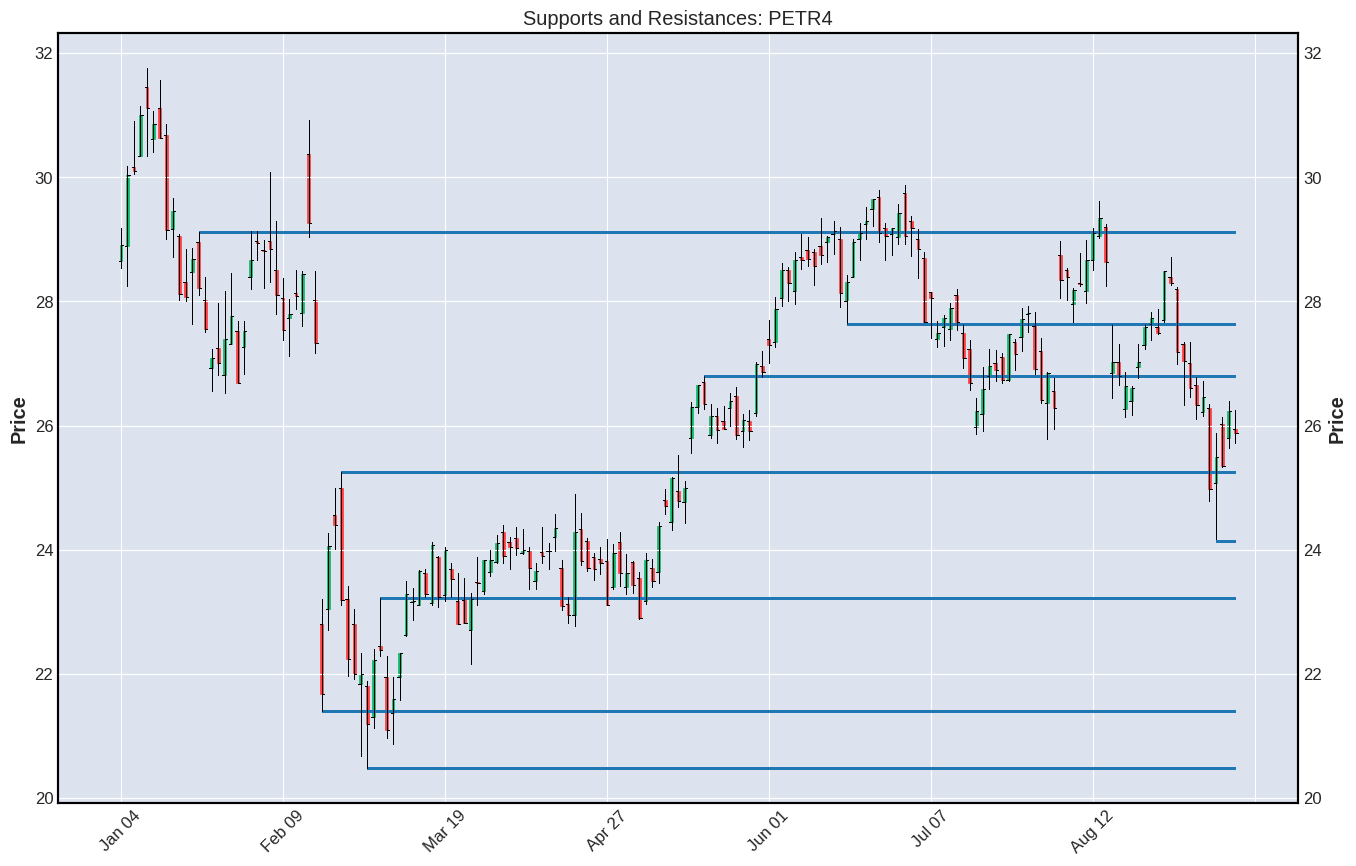
Conclusão
Um dos pilares da análise técnica no mercado financeiro é o entendimento das tendências, e a compreensão dos níveis de suportes e resistências é muito útil.
Você pode reparar pelo gráfico acima que fundos anteriores, que de uma certa forma indicam zonas de suporte, quando perdidos acabam representando zonas de resistência no futuro (e vice versa). Por isso se faz tão importante a análise dessas regiões em paralelo com a tendência do ativo.
Se esse conteúdo te interessa não deixa de se inscrever na nossa NewsLetter e de participar da nossa comunidade no Telegram. Lá você fica sabendo dos posts em primeira mão, além de usufruir de ferramentas como alerta de sinais (de setups como Gap Trap, Saudade de Casa e Estocástico Lento) e resultado de backtests.
Inscreva-se no canal do QuantBrasil!
Acompanhe novidades sobre a plataforma, vídeos sobre finanças quantitativas, tutoriais sobre programação e Inteligência Artificial!