Aprenda a Calcular o IFR — Índice de Força Relativa
O IFR — Índice de Força Relativa — é um indicador de momentum muito utilizado no mercado financeiro. Empregado principalmente para indicar zonas de sobrecompra ou sobrevenda, também pode ser utilizado para apontar divergências entre o preço do ativo e o indicador.
A primeira parte desse artigo tem como objetivo demonstrar como calcular o IFR utilizando pandas, e plotá-lo através da biblioteca matplotlib. É importante entender o cálculo do IFR, já que nos próximos posts iremos utilizá-lo para fundamentar algumas análises e realizar o backtest de estratégias.
Entendendo o IFR
O IFR de um ativo nada mais é do que a razão entre suas variações positivas () e sua variação total (), ao longo de um período específico, em uma escala de 0 a 100.
De acordo com J. Welles Wilder, criador do indicador, os parâmetros recomendados para análise são um período de 14 dias, ao passo que valores acima de 70 sugerem um ativo sobrecomprado e abaixo de 30 indicam um ativo sobrevendido.
Embora os parâmetros acima sejam tradicionalmente utilizados, é possível utilizar diferentes combinações de períodos e níveis de sobrecompra e sobrevenda em diversas estratégias de trading.
A fórmula para calcular o IFR se dá por:
onde a razão é conhecida como Força Relativa (FR).
A Força Relativa
O objetivo da Força Relativa é mostrar quanto um ativo variou positivamente em relação à sua variação total dentro de um determinado período. No entanto, essa variação pode ser calculada de diferentes formas. As duas mais comuns recebem os nomes de Simples e Clássica e podem ser observadas em diferentes softwares de trading, como o Profit.
Força Relativa Simples
O cálculo da Força Relativa Simples se dá pela soma de todas as variações positivas (ganhos) no período analisado, dividida pelo módulo da soma de todas as variações negativas (perdas) no período analisado.
De forma geral, podemos definir:
Onde é o ganho médio em períodos para o -ésimo elemento e é a perda média em períodos para o -ésimo elemento.
Embora não seja tradicionalmente utilizada, a Força Relativa Simples é importante para o cálculo da Força Relativa Clássica.
Força Relativa Clássica
A forma de cálculo proposta pelo criador J. Welles Wilder recebe o nome de Força Relativa Clássica. Nela, a FR é suavizada, criando o mesmo efeito que uma média móvel exponencial tem em relação à média móvel simples.
Onde é o ganho médio anterior em períodos, é a perda média anterior em períodos, é o ganho atual e é a perda atual.
Uma vez que a pressupõe que haja ganhos e perdas médias anteriores, o primeiro valor é calculado da mesma forma que a .
Agora que já entendemos a fórmula por trás do IFR, vamos calculá-lo utilizando Python.
Importando as bibliotecas
O primeiro passo é importar as bibliotecas de interesse. Se você é iniciante em Python e DataScience, não deixe de ler o primeiro post dessa série, onde explicamos com mais detalhes como qualquer um pode começar na análise quantitativa.
# %%capture means we suppress the output
%%capture
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
!pip install yfinance
import yfinance as yfAquisição de dados
Em seguida, faremos o download de um ativo qualquer utilizando a biblioteca do Yahoo Finance.
stock = yf.download('PETR4.SA', start='2020-01-01', end="2020-11-30")[["Adj Close"]]
stock
[*********************100%***********************] 1 of 1 completed
| Adj Close | |
|---|---|
| Date | |
| 2020-01-02 | 30.697731 |
| 2020-01-03 | 30.447748 |
| 2020-01-06 | 30.807720 |
| 2020-01-07 | 30.687731 |
| 2020-01-08 | 30.497744 |
| ... | ... |
| 2020-11-23 | 25.100000 |
| 2020-11-24 | 26.219999 |
| 2020-11-25 | 26.250000 |
| 2020-11-26 | 25.820000 |
| 2020-11-27 | 25.889999 |
226 rows × 1 columns
Calculando a variação do preço do ativo em cada dia
Para calcular a FR, nós temos primeiro que computar quanto o preço do ativo variou em cada dia. Para isso, iremos utilizar o método .diff(), que calcula a diferença de um elemento do dataframe em comparação a outro (por padrão, a linha anterior).
Portanto, ao submetermos a coluna do preço de fechamento ao método .diff(), criamos uma nova coluna que será a variação do preço em cada dia. Como a variação pressupõe pelo menos dois dias, vamos aproveitar para remover a primeira linha do dataframe.
stock['Variation'] = stock['Adj Close'].diff()
stock = stock[1:] # remove first row once it does not have a variation
stock.head()| Adj Close | Variation | |
|---|---|---|
| Date | ||
| 2020-01-03 | 30.447748 | -0.249983 |
| 2020-01-06 | 30.807720 | 0.359972 |
| 2020-01-07 | 30.687731 | -0.119989 |
| 2020-01-08 | 30.497744 | -0.189987 |
| 2020-01-09 | 30.397753 | -0.099991 |
Agora, vamos separar as variações positivas e negativas em duas novas colunas, Gain e Loss. Nós faremos isso utilizando a função np.where, na qual iremos escrever a lógica através da estrutura np.where(condition, x, y) onde se a condição for verdadeira, retorna-se xxx, e se falsa, retorna-se yyy.
Dessa forma, para a coluna de ganhos o raciocínio é o seguinte: se a variação for positiva (> 0), preenchemos com o valor da variação; caso contrário preenchemos com 0. Assim como para a coluna de perdas: se a variação for negativa (< 0), preenchemos com o valor da variação, senão preenchemos com 0.
stock['Gain'] = np.where(stock['Variation'] > 0, stock['Variation'], 0)
stock['Loss'] = np.where(stock['Variation'] < 0, stock['Variation'], 0)
stock
| Adj Close | Variation | Gain | Loss | |
|---|---|---|---|---|
| Date | ||||
| 2020-01-03 | 30.447748 | -0.249983 | 0.000000 | -0.249983 |
| 2020-01-06 | 30.807720 | 0.359972 | 0.359972 | 0.000000 |
| 2020-01-07 | 30.687731 | -0.119989 | 0.000000 | -0.119989 |
| 2020-01-08 | 30.497744 | -0.189987 | 0.000000 | -0.189987 |
| 2020-01-09 | 30.397753 | -0.099991 | 0.000000 | -0.099991 |
| ... | ... | ... | ... | ... |
| 2020-11-23 | 25.100000 | 1.280001 | 1.280001 | 0.000000 |
| 2020-11-24 | 26.219999 | 1.119999 | 1.119999 | 0.000000 |
| 2020-11-25 | 26.250000 | 0.030001 | 0.030001 | 0.000000 |
| 2020-11-26 | 25.820000 | -0.430000 | 0.000000 | -0.430000 |
| 2020-11-27 | 25.889999 | 0.070000 | 0.070000 | 0.000000 |
225 rows × 4 columns
Calculando a média de ganhos e perdas
Para calcularmos a média, precisamos apenas de duas funções combinadas:
rolling(n), que cria janelas móveis de nnn períodos e;mean(), que calcula a média de um conjunto de valores.
Vale ressaltar que a média das perdas é dado pelo seu módulo, portanto iremos usar também a função abs() para retornar seu valor absoluto.
n = 14 # define window interval
simple_avg_gain = stock['Gain'].rolling(n).mean()
simple_avg_loss = stock['Loss'].abs().rolling(n).mean()Uma vez que temos o ganho e a perda média simples calculados, podemos calcular o ganho e a perda média clássica. Como dito anteriormente, utilizaremos as médias simples para inicializar o cálculo, e a partir daí calcularemos a razão utilizando o método de Wilder.
Obs: a boa prática de pandas estimula o cálculo vetorial em detrimento de loops sempre que possível. Embora o nesse caso seja menos eficiente, vamos utilizá-lo por simplicidade.
# start off of simple average series
classic_avg_gain = simple_avg_gain.copy()
classic_avg_loss = simple_avg_loss.copy()
# iterate over the new series but only change values after the nth element
for i in range(n, len(classic_avg_gain)):
classic_avg_gain[i] = (classic_avg_gain[i - 1] * (n - 1) + stock['Gain'].iloc[i]) / n
classic_avg_loss[i] = (classic_avg_loss[i - 1] * (n - 1) + stock['Loss'].abs().iloc[i]) / n
Podemos então criar as colunas com o cálculo das Forças Relativas (do inglês, RS, ou Relative Strength), que nada mais são do que a razão entre as médias calculadas a cima. Perceba que apenas após a janela mínima de 14 dias temos o primeiro valor de FR, que o primeiro valor é sempre o mesmo, e que há uma ligeira diferença entre os seguintes.
stock['Simple RS'] = simple_avg_gain / simple_avg_loss
stock['Classic RS'] = classic_avg_gain / classic_avg_loss
stock[['Simple RS', 'Classic RS']].head(20)| Simple RS | Classic RS | |
|---|---|---|
| Date | ||
| 2020-01-03 | NaN | NaN |
| 2020-01-06 | NaN | NaN |
| 2020-01-07 | NaN | NaN |
| 2020-01-08 | NaN | NaN |
| 2020-01-09 | NaN | NaN |
| 2020-01-10 | NaN | NaN |
| 2020-01-13 | NaN | NaN |
| 2020-01-14 | NaN | NaN |
| 2020-01-15 | NaN | NaN |
| 2020-01-16 | NaN | NaN |
| 2020-01-17 | NaN | NaN |
| 2020-01-20 | NaN | NaN |
| 2020-01-21 | NaN | NaN |
| 2020-01-22 | 0.389610 | 0.389610 |
| 2020-01-23 | 0.611650 | 0.557442 |
| 2020-01-24 | 0.373444 | 0.474127 |
| 2020-01-27 | 0.252809 | 0.299316 |
| 2020-01-28 | 0.495549 | 0.540055 |
| 2020-01-29 | 0.525993 | 0.556890 |
| 2020-01-30 | 0.576433 | 0.589524 |
Calculando o IFR
Finalmente, para calcular o IFR (do inglês, RSI, ou Relative Strength Index) vamos simplesmente escrever a fórmula a seguir em uma única linha de código:
stock['Simple RSI'] = 100 - (100 / (1 + stock['Simple RS']))
stock['Classic RSI'] = 100 - (100 / (1 + stock['Classic RS']))
stock[['Simple RSI', 'Classic RSI']].head(20)| Simple RSI | Classic RSI | |
|---|---|---|
| Date | ||
| 2020-01-03 | NaN | NaN |
| 2020-01-06 | NaN | NaN |
| 2020-01-07 | NaN | NaN |
| 2020-01-08 | NaN | NaN |
| 2020-01-09 | NaN | NaN |
| 2020-01-10 | NaN | NaN |
| 2020-01-13 | NaN | NaN |
| 2020-01-14 | NaN | NaN |
| 2020-01-15 | NaN | NaN |
| 2020-01-16 | NaN | NaN |
| 2020-01-17 | NaN | NaN |
| 2020-01-20 | NaN | NaN |
| 2020-01-21 | NaN | NaN |
| 2020-01-22 | 28.037365 | 28.037365 |
| 2020-01-23 | 37.951780 | 35.792132 |
| 2020-01-24 | 27.190330 | 32.163249 |
| 2020-01-27 | 20.179364 | 23.036405 |
| 2020-01-28 | 33.134901 | 35.067237 |
| 2020-01-29 | 34.468921 | 35.769381 |
| 2020-01-30 | 36.565662 | 37.088090 |
Plotando o gráfico do IFR
Utilizando o módulo pyplot da biblioteca Matplotlib, iremos plotar a coluna com os valores de IFR. Como esse indicador varia de 0 a 100, iremos também formatar o eixo y para apresentar sua escala entre esses valores.
Daqui pra frente, toda menção ao IFR será, na verdade, ao IFR clássico, uma vez que este é o padrão da indústria.
plt.title("IFR PETR4")
stock['Classic RSI'].plot()
plt.ylim(0, 100)(0, 100)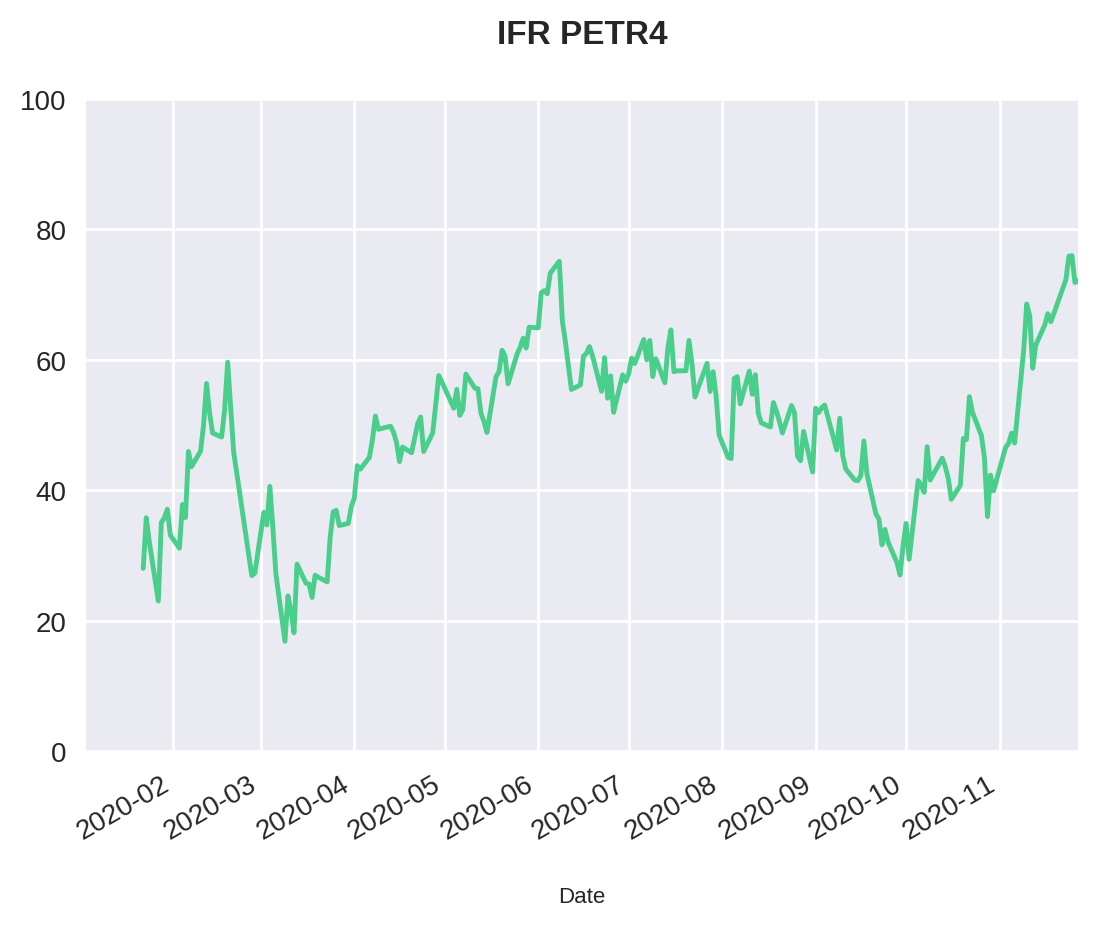
Como mencionado anteriormente, o IFR é popularmente usado para indicar zonas de sobrecompra ou sobrevenda. Dessa forma, vamos plotar linhas indicando esses valores no nosso gráfico. Para isso, vamos utilizar as funções .axhline, que plota uma linha horizontal, e .axhspan, que plota um retângulo (nesse caso, a faixa entre as zonas de sobrecompra e sobrevenda).
plt.title("IFR PETR4")
stock['Classic RSI'].plot()
plt.axhline(y=30, color='black', linestyle='--')
plt.axhline(y=70, color='black', linestyle='--')
plt.axhspan(30, 70, color='thistle')
plt.ylim(0, 100)(0, 100)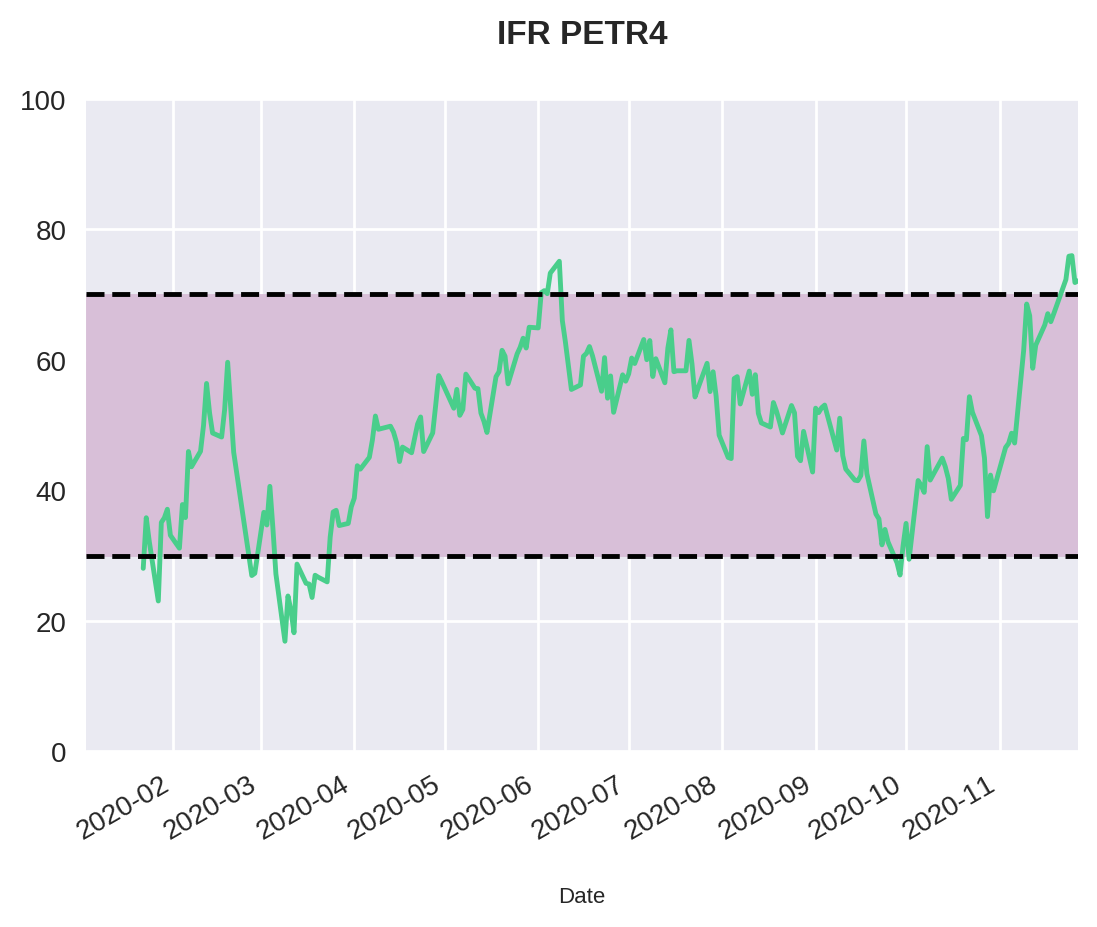
Como o IFR é um indicador que está diretamente relacionado ao preço do ativo, é importante visualizá-los em conjunto. Vamos plotá-los em seguida.
Primeiro, temos que criar um container (fig) que irá receber os dois gráficos (ax1 e ax2). Esses gráficos serão apresentados um seguido do outro (nrows=2), irão compartilhar o eixo x (sharex=True) e a proporção será de 3:1 (gridspec_kw={'height_ratios': [3, 1]}).
fig, (ax1, ax2) = plt.subplots(
nrows=2,
sharex=True,
figsize=(12,8),
gridspec_kw={'height_ratios': [3, 1]})
ax1.plot(stock.index, stock['Adj Close'], label='Fechamento')
ax1.legend()
ax2.plot(stock.index, stock['Classic RSI'], label='IFR', color="#033660")
ax2.axhline(y=70, color='white', linestyle='--')
ax2.axhline(y=30, color='white', linestyle='--')
ax2.axhspan(30, 70, color='indigo', alpha=0.2)
ax2.set_ylim(0, 100)
ax2.legend()<matplotlib.legend.Legend at 0x7f6ee5892710>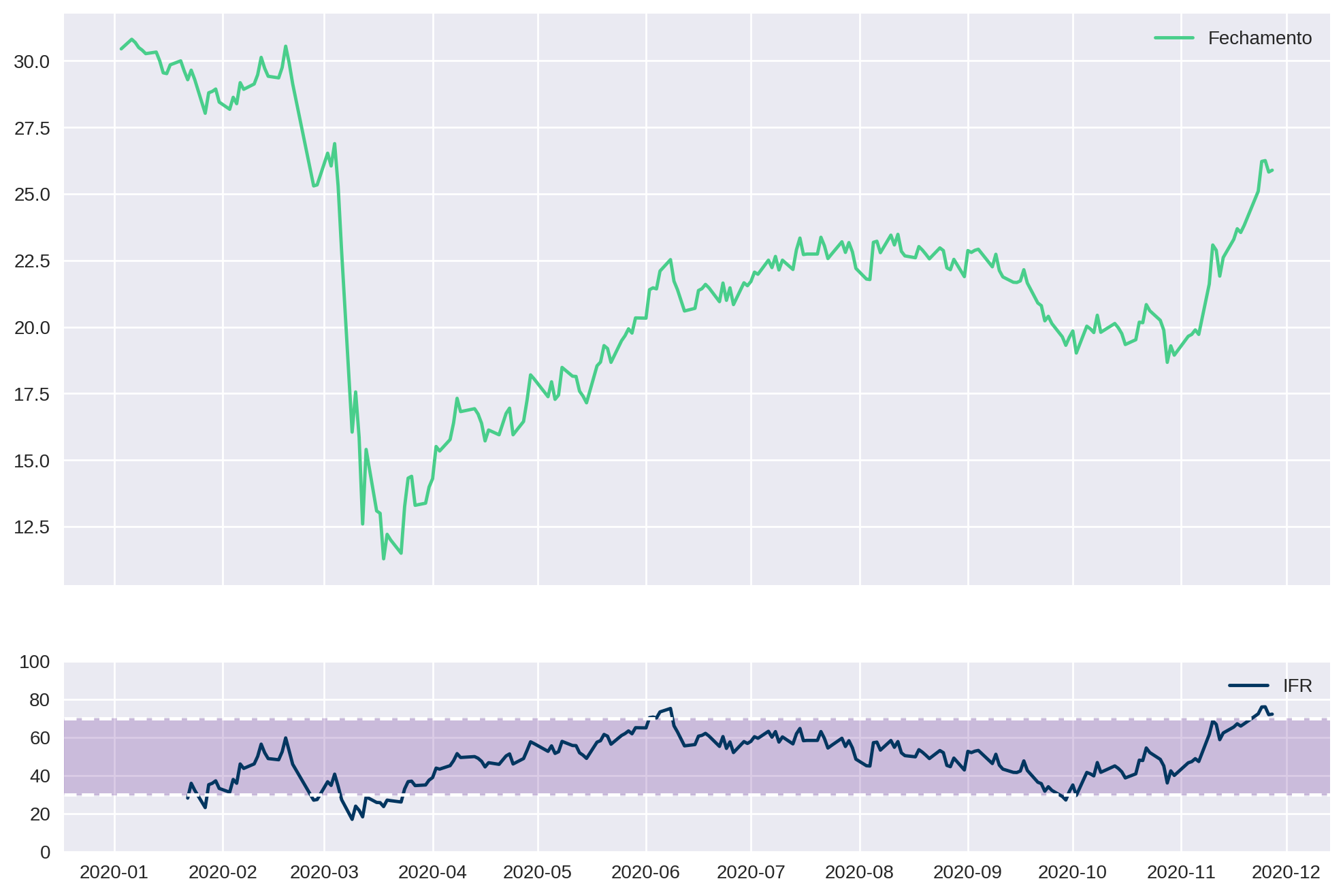
Criando uma função para calcular e plotar o IFR
Por fim, vamos unir tudo que fizemos até agora em uma função para calcular e plotar o preço e IFR de um ativo qualquer. A função receberá os seguintes parâmetros:
- o dataframe
data, com os dados do ativo que você estiver utilizando; - a coluna
column, cujos valores serão extraídos do dataframe e serão utilizados para calcular a média de ganhos e perdas; - a janela de cálculo
window, que terá 14 como valor padrão e; - os níveis de sobrecompra
limit_upe sobrevendalimit_downdo indicador, que terão como padrão 70 e 30, respectivamente.
def plot_RSI(data, column, window=14, limit_up=70.0, limit_down=30.0):
# Establish gains and losses for each day
data['Variation'] = data[column].diff()
data = data[1:]
data['Gain'] = np.where(data['Variation'] > 0, data['Variation'], 0)
data['Loss'] = np.where(data['Variation'] < 0, data['Variation'], 0)
# Calculate simple averages so we can initialize the classic averages
simple_avg_gain = data['Gain'].rolling(window).mean()
simple_avg_loss = data['Loss'].abs().rolling(window).mean()
classic_avg_gain = simple_avg_gain.copy()
classic_avg_loss = simple_avg_loss.copy()
for i in range(window, len(classic_avg_gain)):
classic_avg_gain[i] = (classic_avg_gain[i - 1] * (window - 1) + data['Gain'].iloc[i]) / window
classic_avg_loss[i] = (classic_avg_loss[i - 1] * (window - 1) + data['Loss'].abs().iloc[i]) / window
# Calculate the RSI
RS = classic_avg_gain / classic_avg_loss
RSI = 100 - (100 / (1 + RS))
# Then plot the value alongside the stock price
fig, (ax1, ax2) = plt.subplots(
nrows=2,
sharex=True,
figsize=(12,8),
gridspec_kw={'height_ratios': [3, 1]})
# Plot price data
ax1.plot(data.index, data[column], linewidth=3, label=column)
ax1.legend()
# Plot RSI
ax2.plot(data.index, RSI, label='IFR', color="#033660")
ax2.axhline(y=limit_down, color='white', linestyle='--')
ax2.axhline(y=limit_up, color='white', linestyle='--')
ax2.axhspan(limit_down, limit_up, color='indigo', alpha=0.2)
ax2.set_ylim(0, 100)
ax2.legend()Uma vez que a função está definida, nós podemos reutilizá-la em diversos ativos e parâmetros diferentes:
data = yf.download("VVAR3.SA", start="2020-01-01", end="2020-11-26")
plot_RSI(data=data, column="Adj Close", window=9, limit_up=80, limit_down=20)[*********************100%***********************] 1 of 1 completed
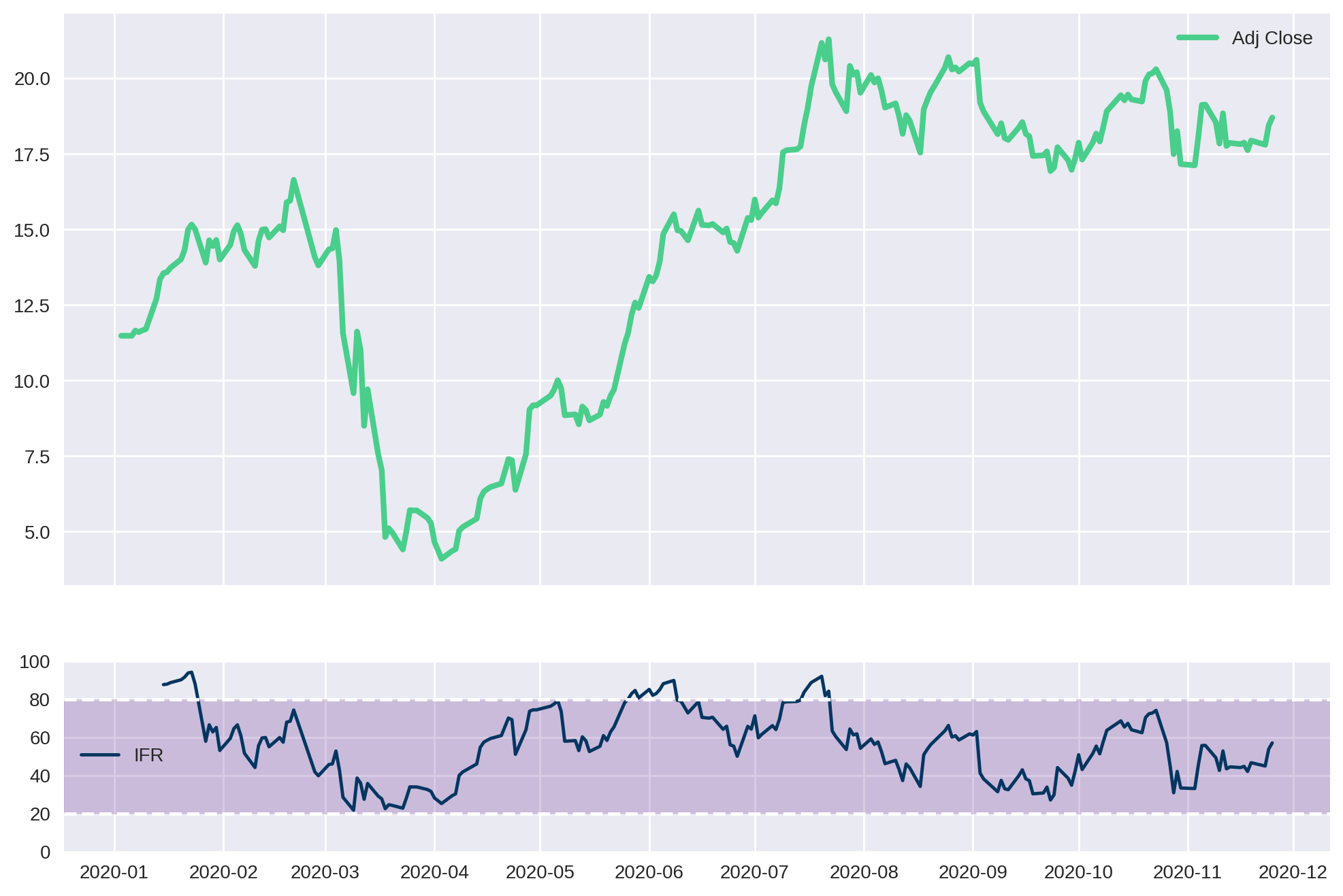
Agora que nós já sabemos como calcular o IFR, podemos iniciar nossos estudos de backtests e estratégias. Não deixe de se inscrever na nossa newsletter para ser avisado dos próximos conteúdos dessa série!
Inscreva-se no canal do QuantBrasil!
Acompanhe novidades sobre a plataforma, vídeos sobre finanças quantitativas, tutoriais sobre programação e Inteligência Artificial!