Analisando a Sazonalidade do Varejo no Mercado Financeiro
No artigo de hoje, vamos abordar um tema que é muito falado e poucas vezes compreendido pelas pessoas: sazonalidade. Antes de tudo, porém, vamos entender o que sazonalidade significa e como ela pode ser aplicada no mercado financeiro.
O que é sazonalidade?
A palavra sazonal deriva-se do latim satio, que por sua vez vem do verbo serere, que significa semear. Não à toa o conceito de sazonalidade está muito atrelado à agricultura. Em outras palavras, sazonalidade é uma caracterista que se repete sempre em uma determinada época do ano.
Por exemplo, durante períodos festivos como Natal, dia das crianças ou até mesmo Black Friday, um aumento nas vendas de varejo é esperada. E esse fato se repete todos os anos.
Efeitos práticos da sazonalidade
No exemplo anterior, vimos um caso específico onde a sazonalidade possui um efeito positivo, ou seja, onde esperamos lucrar com o aumento das vendas no varejo. Contudo, esse nem sempre é o caso. Um clássico exemplo onde a sazonalidade pode interferir negativamente é no caso de uma empresa de sorvetes. Durante o inverno, devido ao clima frio, provavelmente essa venda vai ser baixa. Nesse caso, a sazonalidade implica em uma redução da receita da empresa.
Sazonalidade aplicada ao mercado financeiro
Alguns papéis da bolsa podem possuir "sazonalidade", ou seja, eles podem tender a performar melhor ou pior em determiados períodos do ano. Além dos papéis de varejo, que podem possuir uma sazonalidade durante períodos festivos, outro exemplo são as petroleiras, que são conhecidas por performarem bem no período de inverno do hemisfério norte.
No artigo de hoje, vamos colocar essa sazonalidade à prova e analisar se empresas de varejo performam melhor no último trimestre do ano. Para isso, escolhemos as lojas Renner (LREN3) e o Mercado Livre (MELI) como proxies representando o varejo físico e eletrônico respectivamente.
Definindo nossa hipótese
Existem diversas maneiras de se realizar esse estudo. Um ponto-chave é escolha do período de tempo que vamos utilizar para comparar os resultados. Aqui, vamos tentar provar a hipótese de um melhor último trimestre nas empresas de varejo comparando-o com a variação dos preços das ações no trimestre anterior.
Em outras palavras: vamos comparar as variações de preço dos ativos no 3º e 4º trimestres e observar se há alguma diferença significativa.
Para fortalecer ainda mais o nosso estudo, vamos comparar o retorno obtido pelas Lojas Renner no último trimestre com o índice Bovespa. Isso é importante uma vez que queremos capturar uma possível discrepância do varejo. Ou seja, se LREN3 tiver subido 5% e o IBOV tiver subido 15%, mesmo o ativo de varejo tendo um desempenho positivo, relativamente a performance foi pior.
Durante esse artigo, vamos tentar automatizar o código ao máximo possível. Dessa forma, se você quiser aplicar esse estudo para diferentes ativos em diferentes períodos de tempo, pequenas modificações serão necessárias.
E aí? Será que vamos encontrar alguma sazonalidade interessante no nosso estudo de hoje? Vamos conferir!
Importando as bibliotecas necessárias
Antes de começarmos, vamos importar todas as bibliotecas que iremos usar nese artigo.
import pandas as pd
import numpy as np
import matplotlib.pyplot as pltEstudo de caso: sazonalidade de Lojas Renner
Vamos iniciar nossa análise no varejo importando os dados dos últimos 15 anos de Lojas Renner (LREN3). O arquivo .csv estará disponível no nosso grupo do Telegram.
asset = pd.read_csv('../data/D1/LREN3-D1-sazonalidade.csv', index_col='datetime')
asset
| close | |
|---|---|
| datetime | |
| 2006-07-03 00:00:00 | 3.56 |
| 2006-07-04 00:00:00 | 3.42 |
| 2006-07-05 00:00:00 | 3.17 |
| 2006-07-06 00:00:00 | 3.31 |
| 2006-07-07 00:00:00 | 3.31 |
| ... | ... |
| 2020-12-22 00:00:00 | 42.85 |
| 2020-12-23 00:00:00 | 43.40 |
| 2020-12-28 00:00:00 | 43.65 |
| 2020-12-29 00:00:00 | 43.81 |
| 2020-12-30 00:00:00 | 43.22 |
3584 rows × 1 columns
Para auxiliar nossa análise, vamos criar duas colunas no nosso dataframe. A primeira, chamada month, vai nos retornar o mês e ano de cada linha. Com essa informação, conseguimos identificar se estamos no último dia de cada mês comparando os valores com a linha posterior.
asset["month"] = pd.to_datetime(asset.index).strftime('%Y-%m')
asset["last of month"] = asset["month"] != asset["month"].shift(-1)
asset
| close | month | last of month | |
|---|---|---|---|
| datetime | |||
| 2006-07-03 00:00:00 | 3.56 | 2006-07 | False |
| 2006-07-04 00:00:00 | 3.42 | 2006-07 | False |
| 2006-07-05 00:00:00 | 3.17 | 2006-07 | False |
| 2006-07-06 00:00:00 | 3.31 | 2006-07 | False |
| 2006-07-07 00:00:00 | 3.31 | 2006-07 | False |
| ... | ... | ... | ... |
| 2020-12-22 00:00:00 | 42.85 | 2020-12 | False |
| 2020-12-23 00:00:00 | 43.40 | 2020-12 | False |
| 2020-12-28 00:00:00 | 43.65 | 2020-12 | False |
| 2020-12-29 00:00:00 | 43.81 | 2020-12 | False |
| 2020-12-30 00:00:00 | 43.22 | 2020-12 | True |
3584 rows × 3 columns
Agora vamos criar uma nova coluna com o valor de fechamento do ativo no último dia do mês. O resto dos dias vai receber o valor 0.
asset["value"] = np.where(
(asset["last of month"] == True),
asset["close"],
0
)
asset
| close | month | last of month | value | |
|---|---|---|---|---|
| datetime | ||||
| 2006-07-03 00:00:00 | 3.56 | 2006-07 | False | 0.00 |
| 2006-07-04 00:00:00 | 3.42 | 2006-07 | False | 0.00 |
| 2006-07-05 00:00:00 | 3.17 | 2006-07 | False | 0.00 |
| 2006-07-06 00:00:00 | 3.31 | 2006-07 | False | 0.00 |
| 2006-07-07 00:00:00 | 3.31 | 2006-07 | False | 0.00 |
| ... | ... | ... | ... | ... |
| 2020-12-22 00:00:00 | 42.85 | 2020-12 | False | 0.00 |
| 2020-12-23 00:00:00 | 43.40 | 2020-12 | False | 0.00 |
| 2020-12-28 00:00:00 | 43.65 | 2020-12 | False | 0.00 |
| 2020-12-29 00:00:00 | 43.81 | 2020-12 | False | 0.00 |
| 2020-12-30 00:00:00 | 43.22 | 2020-12 | True | 43.22 |
3584 rows × 4 columns
Podemos agora reduzir o nosso dataframe selecionando apenas as colunas que tem o valor diferente de zero, ou seja, só estamos interessados no último dia de cada mês.
asset_filtered = asset[asset["value"] != 0].copy()
asset_filtered
| close | month | last of month | value | |
|---|---|---|---|---|
| datetime | ||||
| 2006-07-31 00:00:00 | 3.48 | 2006-07 | True | 3.48 |
| 2006-08-31 00:00:00 | 3.52 | 2006-08 | True | 3.52 |
| 2006-09-29 00:00:00 | 3.48 | 2006-09 | True | 3.48 |
| 2006-10-31 00:00:00 | 3.71 | 2006-10 | True | 3.71 |
| 2006-11-30 00:00:00 | 3.93 | 2006-11 | True | 3.93 |
| ... | ... | ... | ... | ... |
| 2020-08-31 00:00:00 | 43.02 | 2020-08 | True | 43.02 |
| 2020-09-30 00:00:00 | 39.30 | 2020-09 | True | 39.30 |
| 2020-10-30 00:00:00 | 37.12 | 2020-10 | True | 37.12 |
| 2020-11-30 00:00:00 | 44.29 | 2020-11 | True | 44.29 |
| 2020-12-30 00:00:00 | 43.22 | 2020-12 | True | 43.22 |
174 rows × 4 columns
Após essas manipulações, podemos facilmente calcular a diferença entre dois valores subsequentes utilizando a função pct_change.
asset_filtered["variation"] = asset_filtered["value"].pct_change()
asset_filtered
| close | month | last of month | value | variation | |
|---|---|---|---|---|---|
| datetime | |||||
| 2006-07-31 00:00:00 | 3.48 | 2006-07 | True | 3.48 | NaN |
| 2006-08-31 00:00:00 | 3.52 | 2006-08 | True | 3.52 | 0.011494 |
| 2006-09-29 00:00:00 | 3.48 | 2006-09 | True | 3.48 | -0.011364 |
| 2006-10-31 00:00:00 | 3.71 | 2006-10 | True | 3.71 | 0.066092 |
| 2006-11-30 00:00:00 | 3.93 | 2006-11 | True | 3.93 | 0.059299 |
| ... | ... | ... | ... | ... | ... |
| 2020-08-31 00:00:00 | 43.02 | 2020-08 | True | 43.02 | 0.057002 |
| 2020-09-30 00:00:00 | 39.30 | 2020-09 | True | 39.30 | -0.086471 |
| 2020-10-30 00:00:00 | 37.12 | 2020-10 | True | 37.12 | -0.055471 |
| 2020-11-30 00:00:00 | 44.29 | 2020-11 | True | 44.29 | 0.193157 |
| 2020-12-30 00:00:00 | 43.22 | 2020-12 | True | 43.22 | -0.024159 |
174 rows × 5 columns
Repare que podemos facilmente adicionar uma nova condição e filtrar apenas as variações em períodos de interesse. Por exemplo:
# example with 2 months for analysis
months = ["2007-09", "2007-10"]
pct_per_month = asset_filtered[asset_filtered["month"].isin(months)]
pct_per_month
| close | month | last of month | value | variation | |
|---|---|---|---|---|---|
| datetime | |||||
| 2007-09-28 00:00:00 | 5.18 | 2007-09 | True | 5.18 | 0.079167 |
| 2007-10-31 00:00:00 | 6.06 | 2007-10 | True | 6.06 | 0.169884 |
E por fim, podemos calcular a média desses resultados:
pct_per_month["variation"].mean() 0.12452541827541819Para facilitar a nossa vida, já que vamos repetir a análise para diferentes ativos, vamos colocar todos os passos anteriores em uma função.
Definindo a nossa função
A função que retorna a média da variação mensal no período que escolhermos está programada abaixo.
def mean_return_per_months(df, months):
# creating a month column
df["month"] = pd.to_datetime(df.index).strftime('%Y-%m')
# defining the last day of the month
df["last of month"] = df["month"] != df["month"].shift(-1)
# if last day of the month, get the close price, else 0
df["value"] = np.where(
(df["last of month"] == True),
df["close"],
0
)
# get the non-zero values
df_filtered = df[df["value"] != 0].copy()
# calculate the difference in percentage between the last day of the months
df_filtered["variation"] = df_filtered["value"].pct_change()
# filter the df to get only the list of months we are interrested on
pct_per_month = df_filtered[df_filtered["month"].isin(months)]
# return the mean of the results
return pct_per_month["variation"].mean() Lojas Renner (LREN3)
Com os dados das Lojas Renner já carregados em nosso DataFrame e a função de cálculo da média de variação criada, podemos facilmente calcular os resultados.
Para isso, vamos criar uma lista: mean_of_semesters, onde vamos armazenar a média do terceiro e quarto trimestre desse ativo. Lembre-se, estamos interessados no último trimestre do ano, pois nele temos o Black Friday e o Natal. Como métrica, escolhemos para esse artigo comparar o último trimestre com o trimestre anterior.
Já que os nossos dados vão de 2006 até 2020, podemos criar um loop para alimentarmos a lista com as médias do período escolhido. Para cada ano, adicionamos a média do trimestre que estamos interessados na lista mean_of_semesters. Por fim, criamos um DataFrame a partir dessa lista.
Importante notar que é computacionalmente mais eficiente criar uma lista, adicionar itens à ela dentro do loop e após o processo transformar a lista num DataFrame, do que criar um DataFrame vazio ou com NaN e ir adicionando linhas a cada iteração.
mean_of_semesters = []
for year in range(2006, 2021):
# third trimester
months = [str(year) + "-07", str(year) + "-08", str(year) + "-09"]
mean_3rd_quarter = mean_return_per_months(asset, months)
# fourth trimester
months = [str(year) + "-10", str(year) + "-11", str(year) + "-12"]
mean_4th_quarter = mean_return_per_months(asset, months)
mean_of_semesters.append((year, mean_3rd_quarter, mean_4th_quarter))
columns = ['year', 'mean_LREN_3rd_quarter', 'mean_LREN_4th_quarter']
df = pd.DataFrame(mean_of_semesters, columns=columns)
df
| year | mean_LREN_3rd_quarter | mean_LREN_4th_quarter | |
|---|---|---|---|
| 0 | 2006 | 0.000065 | 0.072331 |
| 1 | 2007 | 0.008517 | 0.003820 |
| 2 | 2008 | -0.100010 | -0.087783 |
| 3 | 2009 | 0.131699 | 0.094397 |
| 4 | 2010 | 0.059773 | -0.002123 |
| 5 | 2011 | -0.045369 | -0.012644 |
| 6 | 2012 | 0.065236 | 0.057072 |
| 7 | 2013 | 0.002069 | -0.014300 |
| 8 | 2014 | 0.003717 | 0.025179 |
| 9 | 2015 | -0.067250 | -0.021932 |
| 10 | 2016 | 0.015849 | -0.011449 |
| 11 | 2017 | 0.096676 | -0.003819 |
| 12 | 2018 | 0.022914 | 0.115833 |
| 13 | 2019 | 0.023149 | 0.036420 |
| 14 | 2020 | -0.015221 | 0.037843 |
Com o novo DataFrame pronto, podemos facilmente plotar os resultados em forma de barra:
df.plot.bar(
x='year',
y=['mean_LREN_3rd_quarter','mean_LREN_4th_quarter'],
title='LREN3',
label=['3rd quarter mean','4th quarter mean']
)
plt.ylabel('return')
plt.show()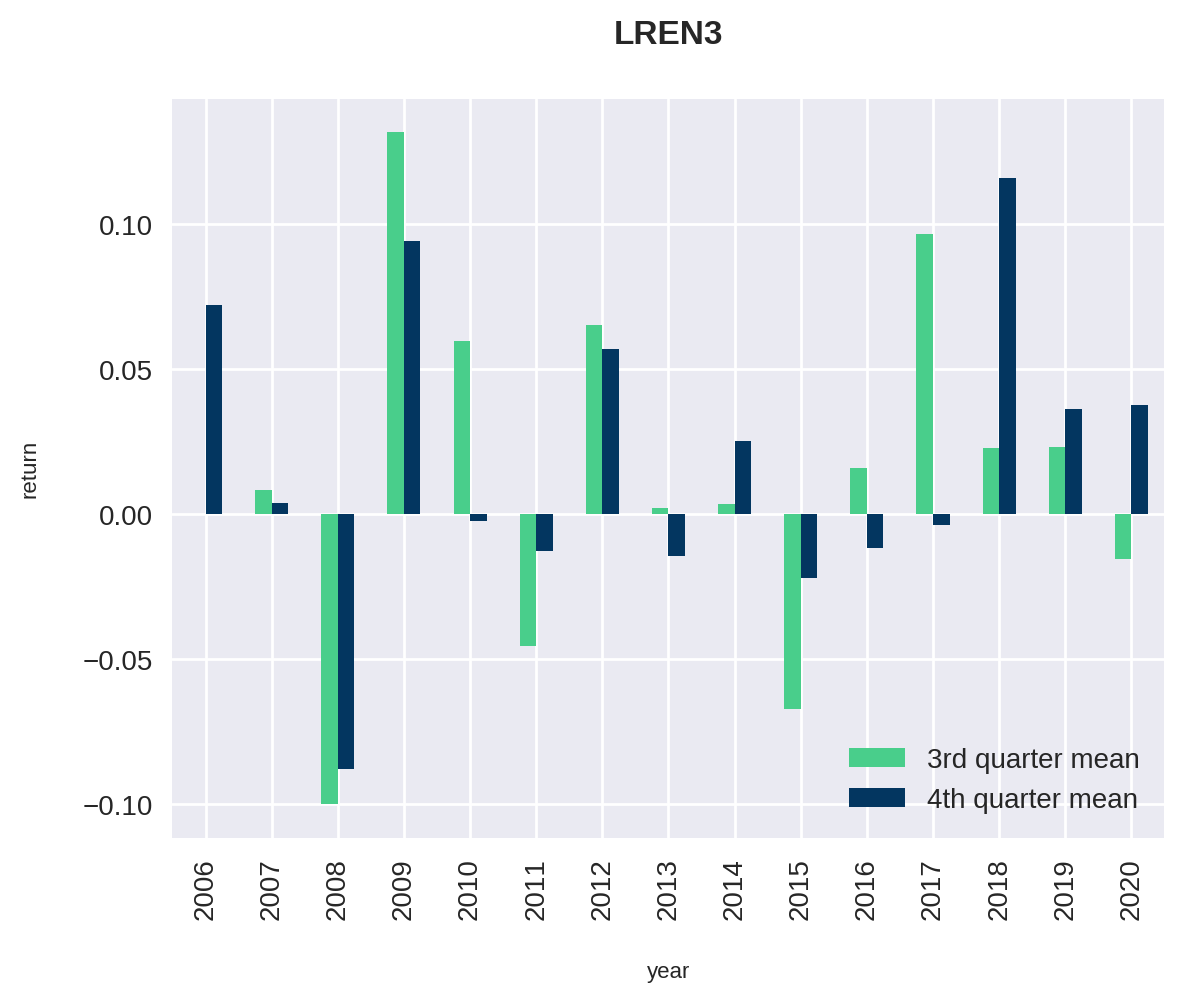
Algumas observações podem ser tiradas dessa análise.
Primeiramente, vimos que nos últimos 3 anos, a variação no quarto trimestre foi sempre positiva e maior do que a variação média do terceiro trimestre.
Outro ponto importante é que, quando houve um terceiro trimestre ruim com variação média negativa, o quarto trimestre fechou melhor (ou menos pior).
Contudo, podemos observar que historicamente existe um equilíbrio entre os trimestres. Enquanto que o quarto trimestre fechou 5 vezes acima do terceiro, em 6 oportunidades o oposto aconteceu.
Comparando com o IBOV
Para fortalecermos a nossa análise, vamos comparar os resultados de LREN3 com o nosso índice, IBOV, para o último trimestre do ano.
Para isso, vamos primeiramente baixar os dados pertinentes do IBOV (novamente, disponível no nosso grupo do Telegram.)
asset = pd.read_csv('../data/D1/IBOV-D1-sazonalidade.csv', index_col='datetime')[["close"]]
asset
| close | |
|---|---|
| datetime | |
| 2006-01-02 | 33507.26 |
| 2006-01-03 | 34540.57 |
| 2006-01-04 | 35002.37 |
| 2006-01-05 | 34936.10 |
| 2006-01-06 | 35475.01 |
| ... | ... |
| 2021-10-14 | 113185.50 |
| 2021-10-15 | 114648.00 |
| 2021-10-18 | 114428.20 |
| 2021-10-19 | 110672.80 |
| 2021-10-20 | 110786.40 |
3906 rows × 1 columns
Uma vez que já temos nossa função programada, só precisamos repetir o último passo da análise anterior e criarmos o loop para o período escolhido. Vamos também usar o comando pd.merge para juntarmos o DataFrame do IBOV com o DataFrame contendo os resultados de LREN3. Escolhemos a opção on='year' para juntarmos os resultados pelo ano.
mean_of_semesters = []
for year in range(2006, 2021):
# fourth trimester
months = [str(year) + "-10", str(year) + "-11", str(year) + "-12"]
mean_4th_quarter = mean_return_per_months(asset, months)
mean_of_semesters.append((year, mean_4th_quarter))
df = pd.merge(
df,
pd.DataFrame(mean_of_semesters,columns=['year','mean_IBOV_4th_quarter']),
on='year'
)
df
| year | mean_LREN_3rd_quarter | mean_LREN_4th_quarter | mean_IBOV_4th_quarter | |
|---|---|---|---|---|
| 0 | 2006 | 0.000065 | 0.072331 | 0.068591 |
| 1 | 2007 | 0.008517 | 0.003820 | 0.018335 |
| 2 | 2008 | -0.100010 | -0.087783 | -0.079875 |
| 3 | 2009 | 0.131699 | 0.094397 | 0.037608 |
| 4 | 2010 | 0.059773 | -0.002123 | -0.000154 |
| 5 | 2011 | -0.045369 | -0.012644 | 0.029244 |
| 6 | 2012 | 0.065236 | 0.057072 | 0.010670 |
| 7 | 2013 | 0.002069 | -0.014300 | -0.004876 |
| 8 | 2014 | 0.003717 | 0.025179 | -0.025021 |
| 9 | 2015 | -0.067250 | -0.021932 | -0.012530 |
| 10 | 2016 | 0.015849 | -0.011449 | 0.012913 |
| 11 | 2017 | 0.096676 | -0.003819 | 0.010104 |
| 12 | 2018 | 0.022914 | 0.115833 | 0.035862 |
| 13 | 2019 | 0.023149 | 0.036420 | 0.033853 |
| 14 | 2020 | -0.015221 | 0.037843 | 0.081705 |
A fim de compararmos os resultados de LREN3 com o IBOV, vamos calcular a diferença entre eles.
Para isso, criamos uma nova coluna no nosso dataFrame contendo a diferença entre o 4º trimestre de LREN3 com o 4º trimestre do IBOV.
df['diff_4th_quarter_LREN_IBOV'] = df['mean_LREN_4th_quarter'] - df['mean_IBOV_4th_quarter']
df
| year | mean_LREN_3rd_quarter | mean_LREN_4th_quarter | mean_IBOV_4th_quarter | diff_4th_quarter_LREN_IBOV | |
|---|---|---|---|---|---|
| 0 | 2006 | 0.000065 | 0.072331 | 0.068591 | 0.003741 |
| 1 | 2007 | 0.008517 | 0.003820 | 0.018335 | -0.014515 |
| 2 | 2008 | -0.100010 | -0.087783 | -0.079875 | -0.007909 |
| 3 | 2009 | 0.131699 | 0.094397 | 0.037608 | 0.056788 |
| 4 | 2010 | 0.059773 | -0.002123 | -0.000154 | -0.001970 |
| 5 | 2011 | -0.045369 | -0.012644 | 0.029244 | -0.041888 |
| 6 | 2012 | 0.065236 | 0.057072 | 0.010670 | 0.046402 |
| 7 | 2013 | 0.002069 | -0.014300 | -0.004876 | -0.009424 |
| 8 | 2014 | 0.003717 | 0.025179 | -0.025021 | 0.050200 |
| 9 | 2015 | -0.067250 | -0.021932 | -0.012530 | -0.009402 |
| 10 | 2016 | 0.015849 | -0.011449 | 0.012913 | -0.024362 |
| 11 | 2017 | 0.096676 | -0.003819 | 0.010104 | -0.013923 |
| 12 | 2018 | 0.022914 | 0.115833 | 0.035862 | 0.079971 |
| 13 | 2019 | 0.023149 | 0.036420 | 0.033853 | 0.002567 |
| 14 | 2020 | -0.015221 | 0.037843 | 0.081705 | -0.043863 |
Novamente podemos plotar facilmente os resultados:
diff = df.copy().set_index('year')['diff_4th_quarter_LREN_IBOV']
diff.plot(
kind="bar",
color=(diff > 0).map({True: '#49ce8b',False: '#d64242'}),
title='Diferença de Retorno LREN3 vs IBOV (4º Tri)',
);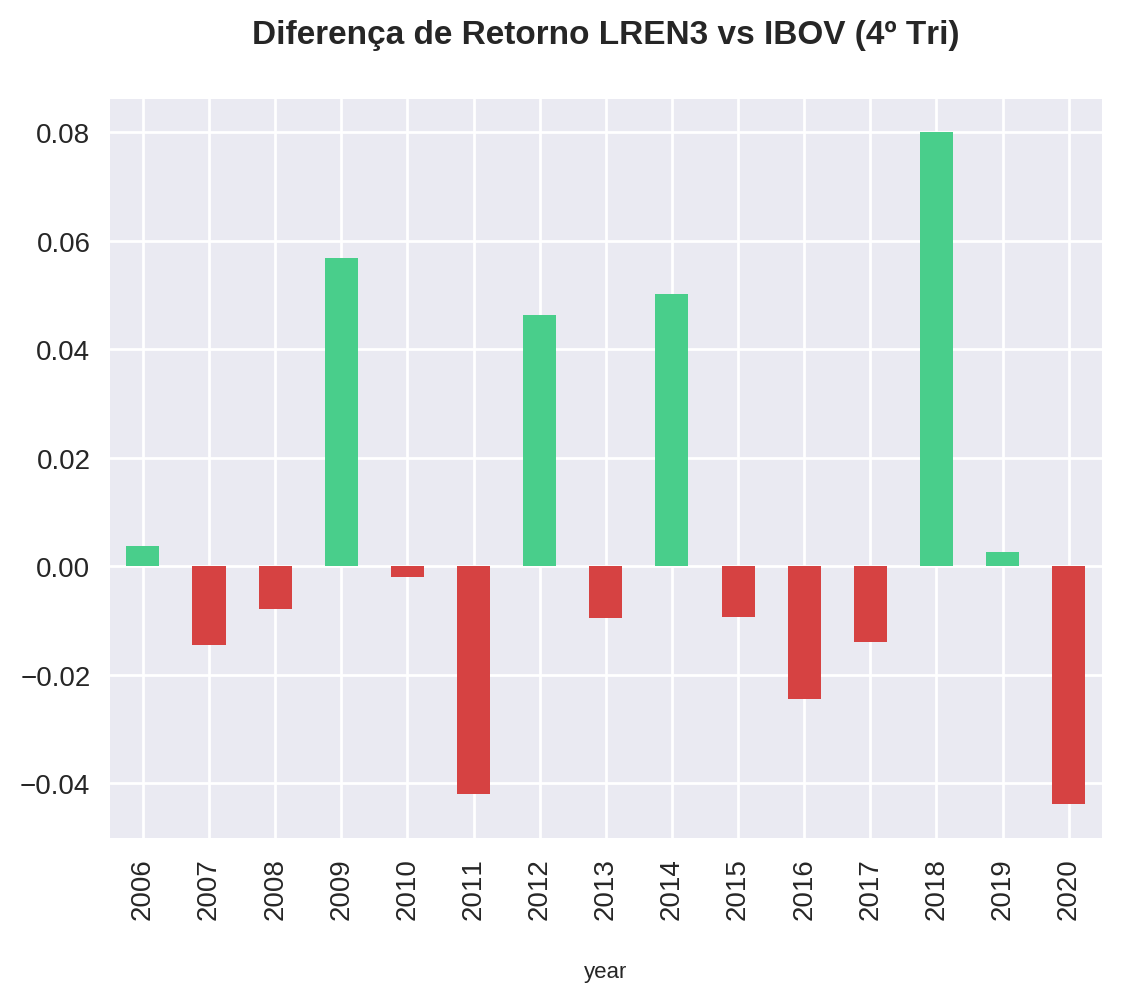
Nos últimos 6 anos, apenas em 2018 as Lojas Renner tiveram uma variação significativamente maior que o IBOV. Na nossa amostragem de 15 anos, LREN3 obteve uma variação média maior que o IBOV no último trimestre em 6 oportunidades.
No entanto, as maiores diferenças estão quando LREN3 bate o IBOV, chegando a quase 8% de diferença em 2018.
Estudo de caso: sazonalidade de Mercado Livre
Vamos finalizar a nossa análise analisando um ativo de varejo eletrônico, MELI. Os dados são os preços listados na NASDAQ, não a BDR, e também estarão disponíveis no nosso grupo do Telegram.
asset = pd.read_csv('../data/D1/MELI-D1-sazonalidade.csv', index_col='datetime')[['close']]
asset
| close | |
|---|---|
| datetime | |
| 2007-08-09 | 17.440 |
| 2007-08-10 | 27.616 |
| 2007-08-13 | 30.669 |
| 2007-08-14 | 29.099 |
| 2007-08-15 | 27.675 |
| ... | ... |
| 2020-12-24 | 1690.480 |
| 2020-12-28 | 1663.720 |
| 2020-12-29 | 1673.490 |
| 2020-12-30 | 1712.940 |
| 2020-12-31 | 1675.220 |
3373 rows × 1 columns
Novamente, como já temos a nossa função programada, apenas repetimos o último passo para analisar o terceiro e quarto trimestre dos últimos 14 anos.
mean_of_semesters = []
for year in range(2007, 2021):
# third trimester
months = [str(year) + "-07", str(year) + "-08", str(year) + "-09"]
mean_3rd_quarter = mean_return_per_months(asset, months)
# fourth trimester
months = [str(year) + "-10", str(year) + "-11", str(year) + "-12"]
mean_4th_quarter = mean_return_per_months(asset, months)
mean_of_semesters.append((year,mean_3rd_quarter, mean_4th_quarter))
columns = ['year', 'mean_MELI_3rd_quarter', 'mean_MELI_4th_quarter']
df = pd.DataFrame(mean_of_semesters, columns=columns)
df
| year | mean_MELI_3rd_quarter | mean_MELI_4th_quarter | |
|---|---|---|---|
| 0 | 2007 | 0.289442 | 0.307803 |
| 1 | 2008 | -0.146742 | -0.031678 |
| 2 | 2009 | 0.128759 | 0.120161 |
| 3 | 2010 | 0.111936 | -0.024727 |
| 4 | 2011 | -0.117243 | 0.155292 |
| 5 | 2012 | 0.037076 | -0.010898 |
| 6 | 2013 | 0.079529 | -0.068355 |
| 7 | 2014 | 0.052978 | 0.065074 |
| 8 | 2015 | -0.135754 | 0.087248 |
| 9 | 2016 | 0.096012 | -0.054002 |
| 10 | 2017 | 0.015879 | 0.072397 |
| 11 | 2018 | 0.046667 | -0.043407 |
| 12 | 2019 | -0.033442 | 0.014822 |
| 13 | 2020 | 0.035422 | 0.159825 |
E plotamos a variação média dos últimos trimestres também em um gráfico de barras.
df.plot.bar(
x='year',
y=['mean_MELI_3rd_quarter', 'mean_MELI_4th_quarter'],
title='MELI',
label=['3rd quarter mean', '4th quarter mean']
)
plt.ylabel('return')
plt.show()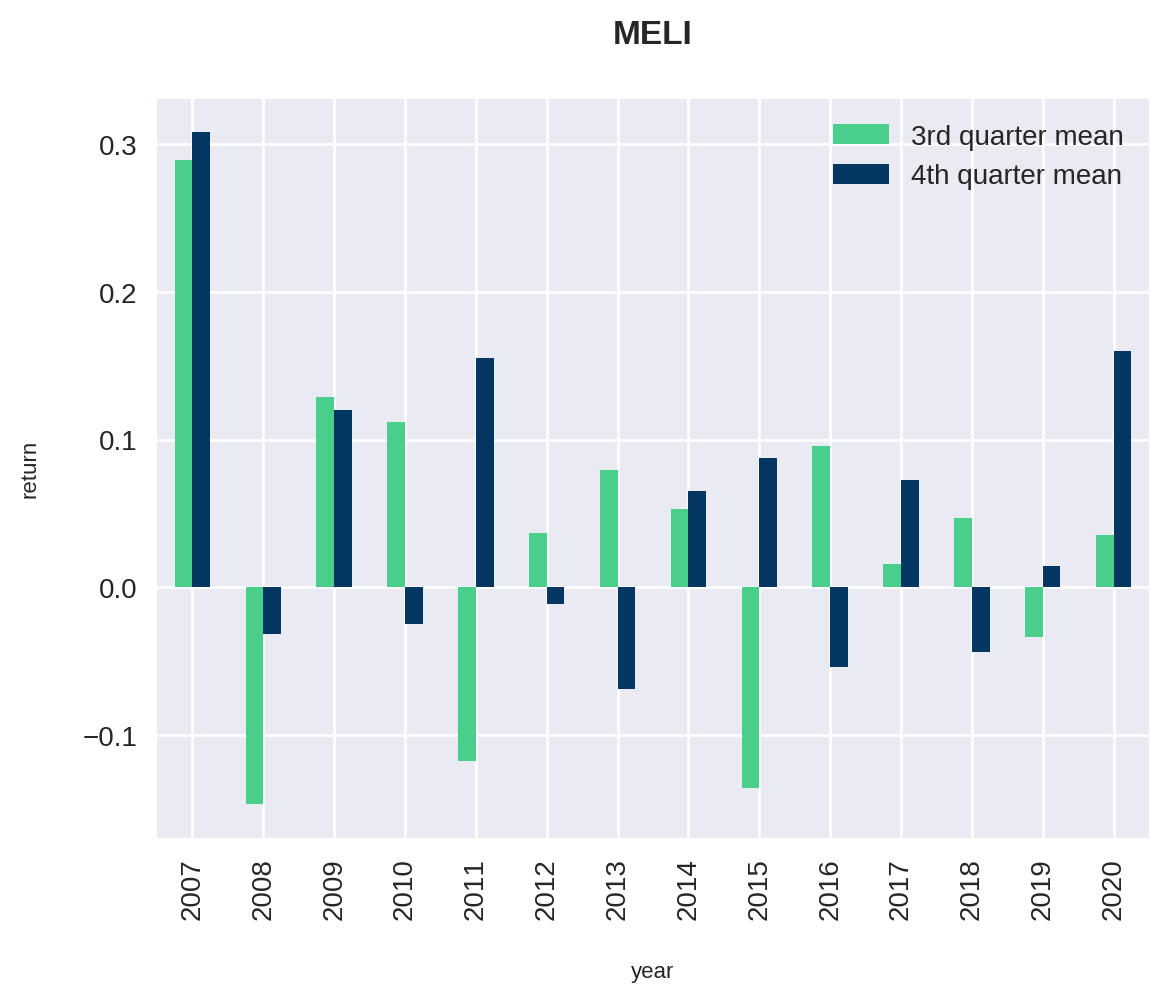
Aqui também vemos um equilíbro, sendo que em 8 vezes a média do último trimestre foi maior que a do terceiro.
Contudo, a média de retorno do quarto trimestre foi positiva e maior que a do terceiro trimestre em 5 dos último 7 anos. Destaque para o ano passado, onde o retorno médio do último trimestre foi o segundo maior da série analisada.
Conclusão
Para esse nosso primeiro estudo de sazonalidade, analisamos o mercado de varejo onde escolhemos Lojas Renner (LREN3) e Mercado Livre (MELI) como os nossos ativos.
Para LREN3, observamos uma pequena vantagem do último trimestre em cima do terceiro, mais especificamente nos últimos 3 anos.
Contudo, vimos também que a média de retorno do índice Bovespa no último trimestre do ano foi positiva nos últimos 5 anos, e melhor que o retorno dos ativos LREN3 em 4 dos últimos 6 anos, perdendo em 2018 e 2019.
Já MELI mostrou uma média de retorno positiva no quarto trimestre e maior que o trimestre anterior em 5 dos últimos 7 anos, sinalizando um possível período positivo para esse papel no último trimestre.
Será que algum outro ativo de varejo performaria melhor que esses dois analisados hoje nesse período? Você consegue pensar em algum outro período melhor para comparar os resultados? Fique à vontade para brincar com o código, escolhendo seu ativo e período de preferência para fazer sua própria análise!
Para um próximo artigo, vamos analisar a hipótese de um aumento nas ações de petróleo durante o inverno do hemisfério norte. Por isso, não se esqueça de entrar no nosso grupo do Telegram e se inscrever na nossa newsletter abaixo para receber notificações sobre artigos novos!
Inscreva-se no canal do QuantBrasil!
Acompanhe novidades sobre a plataforma, vídeos sobre finanças quantitativas, tutoriais sobre programação e Inteligência Artificial!